2.2 基于促进剂的时间活性膜P系统求解SAT问题半统一解
定义2.3：SAT问题可简单表述为，给定一个CNF的布尔公式，判定是否存在一组变量赋值使得该布尔公式的值为真。
众所周知，SAT问题是一个NP完全问题，包含n个变量的布尔公式并具有2n种不同赋值。通过膜分裂，可以在n步内获得2n个膜。此外，通过膜系统的极大并行性特性，可以获得NP完全问题的多项式时间解（甚至线性时间解）。
下面简单介绍通过P系统求解SAT问题的一般思路。首先，通过膜分裂使相应的膜一分为二。然后，分别对新产生膜中的布尔变量x1进行赋值（“真”和“假”），然后对CNF公式中的各个子句进行检查。如果赋值满足CNF公式中的一些子句，则将这些子句序号保存下来。接着继续通过膜分裂的方法使得所有的膜一分为二，同样对变量赋值并检查每个子句。最后，将会在每个膜上产生检查的结果。这时如果在一个膜中包含所有子句的对象序列，则说明这个膜中的解为一个可满足解，即在这种情况下，该CNF公式是可满足的；否则，该CNF公式是不可满足的。
在本节中，将通过基于促进剂的时间活性膜P系统构造出SAT问题的半统一解。
定理2.1：SAT问题可以通过基于促进剂的时间活性膜P系统在线性RS步内通过膜分裂以半统一方式解决。其中，该系统使用a、b、c、e类规则，并且膜上仅有两类电荷。
证明：对于具有n个布尔变量和m个子句的公式，本章考虑命题公式γ＝C1∧C2∧…∧Cm，其中，Cj＝yj，1∨…∨yj，pj，yj，i∈｛xk，－xk|1≤k≤n｝，1≤j≤m，1≤i≤pj，－xk是命题变量xk的否定形式。对于公式γ，P系统构造如下：
其中，O代表字母表：
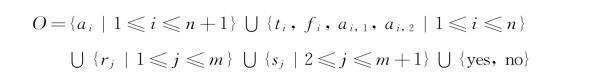
对象ti表示变量xi的赋值为真（true），对象fi表示变量xi的赋值为假（false）；对象rj表示变量赋值使得子句j是可满足的；物质yes表示CNF公式是可满足的，而物质no表示CNF公式是不满足的。
另外，H＝｛1，2｝为膜标签的集合；
为初始膜结构；w1＝no，w2＝a1是各个膜内初始物质；iout＝0是保存最后计算结果的输出区域；通过时间映射e：R→N来指定每条规则的执行时间，其中R是
中的规则有限集。对于R中的规则Ri，其执行时间可以表示为e（Ri）。R包含以下规则集。
（1）产生阶段：
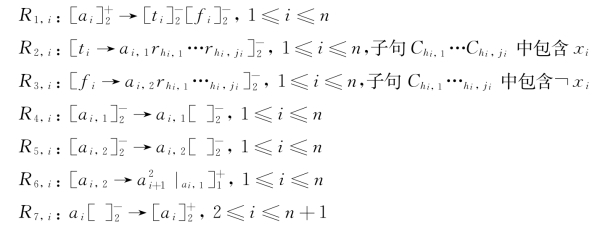
（2）检测阶段：
（3）输出阶段：
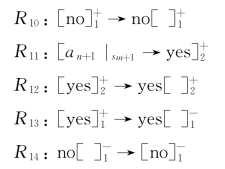
该计算过程分为以下几个阶段。
（1）产生阶段：将膜2分裂成两个新膜，该过程循环执行直至所有可能的候选解都在这些膜中产生。最后，将会产生2n个膜标签为2的膜。
（2）检测阶段：系统检查是否存在一个膜中一组变量的赋值可以满足所有子句。如果存在该变量赋值序列，则说明该CNF公式是可满足的；否则该CNF公式是不满足的。
（3）输出阶段：系统根据检测阶段的结果向环境中输出yes或者no作为计算结果。
接下来，将给出系统详细的计算过程。通过该计算过程可以看出基于促进剂的时间活性膜P系统是如何工作的。
1）产生阶段
设e是规则的执行时间。系统在初始状态下，膜1中含有对象no；膜2中含有对象a1，该对象对应于变量x1。
对于给定的含有n个变量和m个子句的布尔公式，设变量为xi，1≤i≤n。一般地，膜2中的对象ai对应于变量xi。包含n个变量的布尔公式具有2n种不同的变量赋值。第一步，系统开始运行，这时规则R 1，1和R10同时开始执行。规则R1，1是分裂规则，将一个原始膜分裂为两个具有相同膜标签的新膜。同时，对象a1进化为t1和f1后分别出现在新生成的膜中。其中，对象t1对应于变量x1的赋值为真，对象f1对应于变量x1的赋值为假。在该过程中，除了规则R1，1和R10之外，没有任何可以执行的规则，因此该过程仅需一个RS步。当规则R 1，1执行结束时，规则R2，1和R3，1同时开始执行。这些规则对应于检查所有子句中变量x1的赋值（真或假）是否是可满足的。因此，在每个膜2中将生成来自集合｛r1，r2，…，rm｝中的一些对象（或没有对象）。此外，还会生成对象a 1，1（resp.，a 1，2）。因为规则R 2，1和R 3，1可能在不同的RS步内执行结束，因此规则R 4，1和R 5，1的执行并不是同时开始的。当R 2，1（resp.，R 3，1）执行结束时，规则R 4，1（resp.，R 5，1）开始应用，通过执行该规则，对象a 1，1（resp.，a 1，2）将被送出膜2。
就规则的执行时间而言，由于系统在时间无关模式下工作，每条规则的执行时间是任意一个从R到N的不同时间映射，显然e（R 2，1）＋e（R 4，1）未必等于e（R 3，1）＋e（R 5，1）。因此，规则R 6，1起到解决规则同步问题的作用。通过应用规则R 6，1，在促进剂a 1，1的作用下，对象a 1，2进化为两份对象a 2。然后通过应用规则R 7，1，每份对象a 2分别进入其中一个膜2内，并将对应膜上的电荷改变为正。
当变量x i（1≤i≤n）的第一次循环执行结束时，膜标签为2的膜中包含一个对象a 2。在对象a 2的作用下，规则R 1，2在每个膜2中同时开始执行产生4个具有相同膜标签为2的新膜。后面的计算过程类似于变量x 1第一次循环计算过程（即从规则R 1，1到R 7，1的执行过程）。以下用“当前变量”表示每次变量循环计算过程中正在执行的变量，其值对应着取值范围1≤i≤n中的某个x i值。系统继续为变量x 2赋值（真和假），可以获得当前变量赋值满足的所有子句。该过程最多需要6个RS步。当变量x i的第二次循环执行结束，系统继续为其余变量赋值。类似地，每个变量持续不断地分裂，寻找当前变量赋值满足的所有子句。一般来说，对于变量x i的第i次循环计算过程（1≤i≤n），当规则R 4，i和R 5，i执行结束的时候，通过应用规则R 6，i，对象a i，2进化为两份对象a i＋1。因此，对象a i＋1的数量和具有膜标签为2的膜的数量是相同的。因此，当应用规则R 7，i时，注意到标签为2的膜上电荷从负变为正。因此，规则R 7，i可以确保每个膜2内都会出现一份对象a i＋1。此外，由于P系统的极大并行性原理，对于所有膜标签为2的膜，规则R 7，i的应用是同时完成的。
应该指出的是，该系统以循环的方式执行上述过程，所有变量将被赋值并找出满足的子句，直到所有变量的循环计算过程执行结束。从R 1，1到R 7，n的可用规则按以下顺序执行。
第一次循环计算过程中规则的执行：
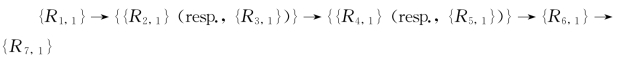
第二次循环计算过程中规则的执行：
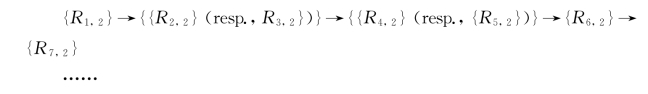
最后一次循环计算过程中规则的执行：
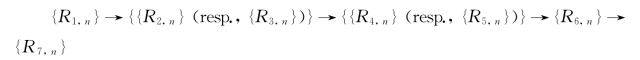
总的来说，系统经过6n个RS步后，产生阶段执行结束。此时，在膜1中可以产生2n个膜标签为2的膜（见图2-1）。
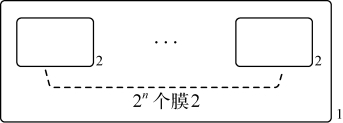
图2-1 产生阶段结束后的膜结构图
2）检测阶段
当对象a n＋1出现在任意一个膜标签为2的膜中时，说明产生阶段所有规则已经执行结束。注意到在每个膜中应用规则R 7，n时遵循极大并行性的原理，因此，每个膜2中的对象a n＋1将同时出现。当产生阶段执行结束时，每个膜标签为2的膜中存在着集合｛r 1，r 2，…，r m｝中的一些对象（或不存在这些对象）。这些对象表示相应的子句在对应变量赋值下是可满足的。显而易见，如果一个膜2中包含集合｛r 1，r 2，…，r m｝中的所有的对象序列，则说明该膜中的解为CNF公式的一个可满足解，即在这种情况下，该CNF公式是可满足的。当膜2中出现对象a n＋1和对象r 1（如果该对象存在）时，通过使用规则R 8，对象r 1进化为s 2。如果对象s j（2≤j≤m）出现在膜2中，可以应用规则R 9，j；当对象sm出现在膜2中时，可以应用规则R 9，m，这时，可以生成对象sm＋1。需要注意的是，整个过程规则在时间无关模式下运行。总的来说，整个检测阶段最多需要m个RS步。
3）输出阶段
当检测阶段结束时，将会有以下两种情况：
（1）肯定的答案：CNF公式是可满足的。在这种情况下，在膜标签为2的膜中生成对象sm＋1，因此可以应用规则R11。通过使用该规则，在膜2中促进剂sm＋1的作用下，对象an＋1进化为物质yes，然后被送出膜外。接下来，规则R12和R13开始执行，最后物质yes被送到环境中，并将该膜1上的电荷改变为负。当规则R10和R13都执行结束，通过使用规则R14，环境中的物质no进入膜1。这样，当P系统停止工作时，物质yes将出现在环境中。因此，该SAT问题至少有一个可满足解。总的来说，输出阶段最多需要4个RS步，这个结果独立于规则的任何时间映射e。
（2）否定的答案：CNF公式是不满足的。在这种情况下，对象sm＋1不会出现在任何一个膜标签为2的膜中。因此，从R11到R14的规则将不会执行。最终，当系统停止时，物质no仍然在环境中，由此可以得出该SAT问题没有可满足解的结论。在这种情况下，该过程不需要RS步。