5.1 内稳态类组织膜系统构建
类组织膜系统是一类分布式并行的计算系统。在原始模型中，细胞之间或细胞与环境之间可以进行物质交流，因此在这类系统中仅有通信规则和细胞分裂规则，而单个细胞内没有对象进化规则。对于环境中初始格局存在的对象，在系统的运行过程中都假定每种对象的数量为无穷多。这样，环境可为细胞提供强大的物质和能量支持。因此，环境在这类系统中发挥着十分重要的作用。实际的生物组织结构如图5-1所示。
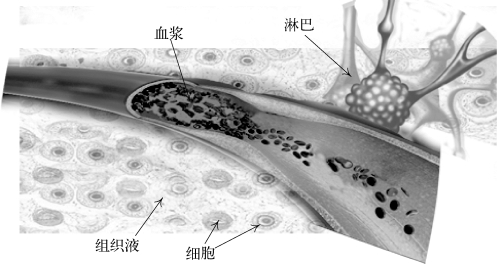
图5-1 实际的生物组织结构
从生物学角度来看，维持体内环境的稳定性是生物提高环境耐受限度的一种主要机制。该机制称为“内稳态”［13］，即生物体控制自身体内环境保持相对稳定，减少对外界条件的依赖，使自身借助于内环境而相对独立于外界环境，从而提高了对生态因子的耐受范围。受到该生物原理的启发，本章将“内稳态”引入类组织膜系统，去除了“环境中对象数量为无穷多”这个假设，使细胞与环境之间尽量不发生物质交换。这样，整个组织系统减少了对环境的依赖，处于“内稳态”状态。于是，本章提出了一种类组织膜系统新的变体，称为基于对象进化规则的内稳态类组织膜系统（简称为内稳态类组织膜系统）。另外，本章将使用促进剂的对象进化规则引入该模型中，单个对象可以在细胞内进化生成某些物质，从而为处于内稳态组织提供一定的物质能量。内稳态类组织模型如图5-2所示。
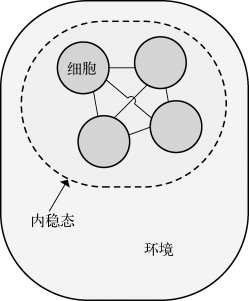
图5-2 内稳态类组织模型
下面将结合生物内稳态模型，分别建立三个内稳态类组织膜系统。
定义5.1：一个度为m（m≥1），基于促进剂和对象进化规则的内稳态类组织膜系统（homeostasis tissue-like P systems with object evolutional rules and promoters，HTP-OEP）可表示如下：
其中，O为对象的字母表；w 0表示在初始状态出现在环境中的物质；w 1，…，w m表示在初始状态下各个细胞内的对象多重集；i out表示输出区域，该区域保存最后的计算结果；R表示规则集合，这些规则包含下面几种类型。
（1）通信规则，称之为该模型的a类规则：
其中i、j∈｛0，1，…，m｝，i≠j，u、v∈O*，pro∈O，|uv|＞0，i和j分别对应区域i和区域j。如果i＝0或者j＝0，则对应的是环境；否则它们对应的是细胞。在促进剂的作用下，当多重集u出现在细胞i中，且多重集v出现在细胞j中，这时，多重集u从细胞i发送到细胞j中，同时多重集v从细胞j发送到细胞i中。如果没有促进剂的作用，那么该规则可以表示为（i，u／v，j）。与类组织膜系统原始模型不同的是，任何格局下环境中物质的数量并不是无限多份。当然，环境中存在的物质也可以和细胞中的物质进行交流。对于这类规则，规则的长度为｜u｜＋｜v｜。
（2）对象进化规则，称之为该模型的b类规则：
其中i∈｛1，…，m｝，a，pro∈O，b∈O*。在促进剂pro的作用下，当一个对象a出现在细胞i中时，在该对象的作用下，其自身进化为多重集b。如果没有促进剂的作用，那么该规则可以表示为［a→b］i。对于这类规则，规则的长度为|a|＋|b|。
（3）细胞分裂规则，称之为该模型的c类规则：
其中i∈｛1，…，m｝，a、b、c∈O，i≠i out。当一个对象a出现在细胞i中时，在该对象的作用下，细胞分裂规则将被应用并开始执行，原始细胞分裂为两个具有相同标签的细胞。在这两个新产生的细胞中，对象a被分别替换成对象b和c，同时原始细胞中的其他物质分别复制到新产生的细胞中。
该模型中包含了通信规则和对象进化规则，但同时还引入了促进剂，使得模型的规则使用条件过于宽泛，从而导致该模型计算能力过于强大。通常，类组织膜系统中只包含通信规则，既可以在通信规则长度很小的情况下达到计算通用性，还可以在时间无关模型下求解NP难问题。现在又同时引入对象进化规则和促进剂，尽管本章考虑环境为空，但所构造的模型限制过于宽泛，计算能力过于强大。定义5.2建立的模型对该模型进行了改进，改进后模型中的规则不再使用促进剂。
定义5.2：一个度为m（m≥1），基于对象进化规则的内稳态类组织膜系统（homeostasis tissue-like P systems with object evolutional rules，为HTPOE）可表示如下：
其中，O为对象的字母表；w 1，…，w m表示在初始状态下各个细胞内的对象多重集；i out表示输出区域，该区域保存最后的计算结果；R表示规则集合，这些规则包含下面几种类型。
（1）通信规则，称之为该模型的a类规则：
其中i、j∈｛0，1，…，m｝，i≠j，u、v∈O*，|uv|＞0，i和j分别对应区域i和区域j。如果i＝0或者j＝0，则对应的是环境；否则它们对应的是细胞。对于这类规则，规则的长度为|u|＋|v|。
（2）对象进化规则，称之为该模型的b类规则：
其中，i∈｛1，…，m｝，a∈O，b∈O*。对于这类规则，规则的长度为|a|＋|b|。为了更好地反映内稳态的生物机制，根据计算复杂度理论，我们规定该类规则的最大规则长度为3，即|a|＋|b|≤3。
（3）细胞分裂规则，称之为该模型的c类规则：
其中，i∈｛1，…，m｝，a、b、c∈O，i≠i out。该规则与定义5.1相同。
定义5.3：一个度为m（m≥1），基于同向／反向进化规则的内稳态类组织膜系统（homeostasis tissue-like P systems with evolutional symport／antiport rules，HTP-ES／A）可表示如下
其中，O为对象的字母表；w 0表示在初始状态出现在环境中的物质；w 1，…，w m表示在初始状态下各个细胞内的对象多重集；i out表示输出区域；R表示规则集合，这些规则包含下面几种类型。
（1）同向进化规则，称之为该模型的a类规则：
其中，i，j∈｛0，1，…，m｝，i≠j，u∈O＋，u′∈O*，|uv|＞0，i和j分别对应区域i和区域j。如果i＝0或者j＝0，则对应的是环境；否则它们对应的是细胞。这类规则执行过程中，当多重集u出现在区域i中（该区域可能是一个细胞或环境），这个多重集会在转移到目标区域j的过程中进化为u′。对于这类规则，规则的长度为|u|＋|u′|。该类规则的执行过程如图5-3所示。
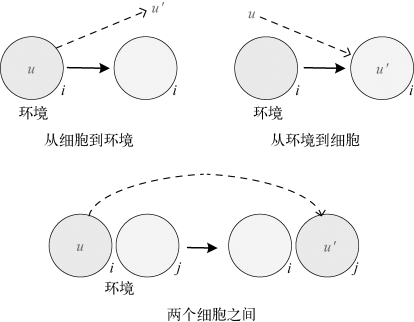
图5-3 同向进化规则执行过程
（2）反向进化规则，称之为该模型的b类规则：
其中i、j∈｛0，1，…，m｝，i≠j，u∈O＋，u′∈O*，|uv|＞0，i和j分别对应区域i和区域j。如果i＝0或者j＝0，则对应的是环境；否则它们对应的是细胞。这类规则执行过程中，当多重集u出现在区域i中（该区域可能是一个细胞或环境），这个多重集会在转移到目标区域j的过程中进化为u′。对于这类规则，规则的长度为|u|＋|u′|。该类规则的执行过程如图5-4所示。
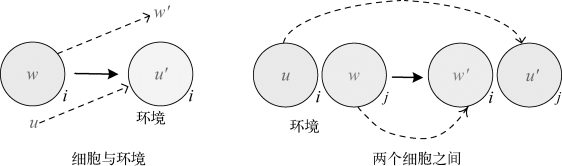
图5-4 反向进化规则执行过程
（3）细胞分裂规则，称之为该模型的c类规则：
其中，i∈｛1，…，m｝，a、b、c∈O，i≠i out。该规则与定义5.1相同。
以上三类模型的系统运行过程都是类似的。对于一个度为m的内稳态类组织膜系统，可以看作由m个细胞作为图的顶点，初始格局由各个区域中的对象多重集来表示。在膜系统计算过程中，各个细胞内以及环境中的对象多重集描述了当前格局。系统从初始格局开始运行，通过执行相应的规则，系统格局将发生变化。从格局C到后继格局C′的过程称为转移，并且用C⇒C′表示，这些有限格局之间的转移称为计算。如果在某个时刻，没有任何规则可应用于当前格局中的对象，而且没有执行中的规则，则计算停止。这时，计算结果会出现在输出区域。系统最大规则长度定义为除细胞分裂规则之外的其他规则的最大长度。
内稳态类组织膜系统在每个区域中以非确定性极大并行的方式应用规则，即在每个计算步，通过非确定性方式应用最大的规则集合。如果某个对象可以同时应用到多个规则中，那么系统只能非确定性地随机选取其中一条规则执行，只有当这条规则执行结束时，该对象才能参与到其他规则的应用中。对于内稳态类组织膜系统，环境中可以存在少量的物质，其数量并不是无限多份。因为系统处于内稳态状态下，细胞与环境基本上不发生物质交流。在这类系统中，不需要环境为细胞提供能量。与原始的类组织模型一样，细胞之间（或者细胞与环境之间）可以进行物质交换，在交换的过程中这些物质保持不变，仅改变物质所在的区域位置。
如果一个内稳态类组织膜系统在时间无关模式下工作，称之为内稳态时间组织膜系统。一个识别内稳态时间组织膜系统定义与前面的定义5.1、定义5.2以及定义5.3是类似的，具体是在以上三个定义中增加下列描述：e是规则有限集合中规则执行时间的映射；i in∈｛1，2，…，m｝表示输入细胞；工作字母表中包含两种物质yes和no，当系统停止时，物质yes或者no必定会出现在输出细胞i out中。
输入多重集（在输入字母表Σ上）添加到输入细胞i in中，就能得到与输入多重集相关联的初始格局。当计算停止时，如果yes（resp.，no）在输出区域中，则为接受计算（resp.，拒绝计算）。
可以通过映射e：R→N来指定每条规则的执行时间，其中R是规则集合，N表示自然数集合。在R中某条规则（如规则r）的执行时间可以表示为e（r）。
对于所有决策问题的集合，用
和
分别表示在标准膜系统下和时间无关模式下可以通过识别基于促进剂和对象进化规则的内稳态类组织膜系统在多项式时间内得到其统一解；同样，用
和
分别表示在标准膜系统下和时间无关模式下可以通过识别基于对象进化规则的内稳态类组织膜系统在多项式时间内得到其统一解；用
和
分别表示在标准膜系统下和时间无关模式下可以通过识别基于同向／反向进化规则的内稳态类组织膜系统在多项式时间内得到其统一解。其中，系统中最大规则长度都为k。