6.2 基于活性膜P系统的CNSMO算法设计
SVM的基本模型为二次凸规划问题,能获得全局最优解,并使用核函数解决高维映射空间的维度灾难问题,所以在很多应用中体现出良好泛化预测能力。但是凸规划问题的核内积构成的N×N维矩阵(N为样本数),其内存需求是训练样本的二次方,因此面对中大规模数据集时,算法的空间复杂度太高。为此,国内外学者提出了分块算法(chunking algorithm)和分解算法(decomposition algorithm)来降低SVM原始算法的内存需求。其中,分块算法将原数据集分成多个子块,分别对各个子块进行训练并去掉其中的非支持向量样本,使得训练样本的大小得到有效缩减。然后,使用支持向量样本来参与训练,从而降低了参与训练的样本数。但是,SVM分块算法由于在复杂数据环境下会损失很多支持向量,所以会降低精度;另外在支持向量较多的数据集中,分块算法对训练样本的缩减能力十分有限。Osuna等人提出了分解算法来应对分块算法的以上缺点。分解算法每次训练的样本数目,即训练窗口大小固定,因此本质上降低了SVM原始模型的内存需求。但是分解算法需要不断迭代来逼近最优决策超平面,所以虽然降低了内存需求,但是收敛时间仍然较长,算法时间复杂度较高。
本节结合活性膜P系统和CNSMO,提出了PAM-CNSMO分类算法。利用膜系统嵌套的膜结构,并将物质进化规则的方法引入该算法中,从而避免使用交叉验证,具有良好的算法效率和稳定性;另外,通过在膜内进行反复迭代和对整体数据验证KKT条件,保留了更多的支持向量,从而获得更好的泛化预测能力。
6.2.1 活性膜P系统基本框架以及进化规则设计
受到活性膜P系统基本框架以及运行机制的启发,本章提出了一种基于活性P膜系统的CNSMO算法PAM-CNSMO。将活性膜P系统中的一些进化规则引入该算法,比如膜创建、膜溶解以及物质进化规则。基于嵌套膜结构,把算法中的各种操作对应于P系统中的规则,利用各个膜中的CNSMO子算法,并且可以将各个子算法的计算结果在相邻的膜之间进行交流。
膜系统主要由膜结构、对象多重集和规则集合组成。本算法中由于采用活性膜P系统,在算法运行过程中其膜结构是可以改变的。膜中的多重集对象可表示多维数据集和决策函数。而规则集合则对应于该算法中一些子算法中相关操作。
P系统构造如下:
![]()
其中,O为对象字母表,表示各个膜中物质的有限集合;H={1,2,3,4}为膜标签的集合;m=[[[]4]2]1为初始膜结构;w i(1≤i≤4)是各个膜内初始物质;w 1内为输入数据集合,w 2=w 4=λ;i in=1是数据的输入区域;i out=4是保存最后计算结果的输出区域;R是规则集,包括物质进化规则、通信规则、膜溶解规则以及膜创建规则等。这些规则对应于系统中子算法中的各种操作算子。膜中物质的多重集可表示多维数据集和决策函数,而物质的进化规则就是对膜内物质进行修改,相当于各个子算法中具体操作后相应数据的变化。
在PAM-CNSMO中,主要有以下几类规则:选择规则、交流规则和进化规则。
(1)选择规则:
根据选择规则,本算法中主要是选取多维的数据集。从候选对象集选取出满足条件的数据集合以后,就可以进入下一步操作。
(2)交流规则与进化规则:
PAM-CNSMO算法运行时,可以完成多种操作,例如在各个膜区域内可以使用通信规则将一些物质从一个膜内转移到相邻的膜内。还可以使用对象进化规则,将膜内的物质生成其他物质,从而实现算法中改变相应数据的操作。以下为受到活性膜P系统规则启发而得到的规则,但需要说明的是,其具体形式与理论模型中的规则有一定的区别。
(1)进化规则,称之为a类规则:
![]()
如果物质a 1a 2…a n出现在膜标签为h的膜中,该规则可以应用于当前配置中。通过应用此规则,会产生多重集b 1b 2…b m。
(2)通信规则1,称之为b类规则:
![]()
物质a 1a 2…a n从膜外进入膜中。同时,膜的极性可以改变,但是其膜标签保持不变。
(3)通信规则2,称之为c类规则:
![]() (https://www.daowen.com)
(https://www.daowen.com)
物质a 1a 2…a n从膜内发送到膜外。同时,膜的极性可以改变,但是其膜标签保持不变;
(4)溶解规则,称之为d类规则:
![]()
在膜中存在物质a 1a 2…a n的情况下,膜可以溶解。溶解的同时,该膜中的物质可以发生改变。
以上规则中,H是膜标签的有限集合,膜上电荷集合为{+,-,0}。
(5)终止规则,称之为e类规则。终止规则规定算法的终止条件。当所有样本都满足KKT条件时算法终止。
图6-2为初始膜结构。各个膜中物质的多重集可表示多维数据集和决策函数,物质可以被修改,并可交流到相邻膜区域内。
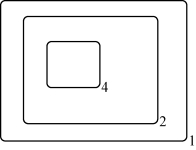
图6-2 初始膜结构
6.2.2 基于活性膜P系统的CNSMO算法设计
受到活性膜P系统中膜结构和进化规则的启发,本章的算法使用嵌套多层膜结构,膜内对应的是相应物质以及子算法。如图6-3中,各个膜内为相应的子算法,每个子算法对应P系统中的一系列对象进化规则。在相邻的膜之间存在着数据交流的通信规则,使得相应的物质实现进化向相应的膜进行传输。其中,最外层为皮肤膜1,皮肤膜内为膜2,最内层膜分别为膜标签为3的膜以及膜4(这些膜都为基本膜)。
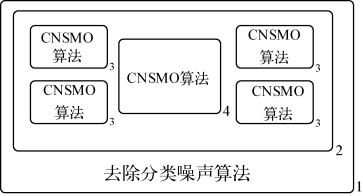
图6-3 各个膜内的子算法
算法的具体计算过程如下,初始时刻,输入系统的数据对应于皮肤膜中的初始物质,即训练数据的样本点集合。首先,使用相对密度的方法去除噪声数据得到数据集D′,在该膜内通过一系列对象进化规则实现“去除分类噪声”子算法,从而去除噪声点数据。然后,使用通信规则将数据集D′发送到膜2中。这样,皮肤膜中的物质就能进入膜2中进行物质更新,该过程体现的是膜系统的通信特征。然后,使用膜创建规则产生标签均为3的n个基本膜,其中n值的大小可根据内存资源条件或者根据实际情况进行人工设定,这里假设为4。数据集D′生成两份数据一致的副本,其中一份保留在膜2中,另外一份进入膜4中将用于数据验证。
膜2中的数据集D′被划分为4份数据(与膜3的膜数量一致),每份数据分别“非确定”地进入其中一个膜3后,再将CNSMO算法作为该膜内的候选算法,其主要操作是提取支持向量。将每个膜3中产生的支持向量集送入膜4得到整体数据的支持向量集合。通过得到的该整体支持向量集合,就能获得分类决策函数,从而可以判断膜4中的数据集D′中是否有违反KKT条件的样本。如果存在违背KKT条件的样本点,则将这些样本点以及整体支持向量集合的副本送出膜4,然后将该数据集(即整体数据的支持向量集合以及违背KKT条件的样本点)进行数据划分,分为4份后再分别进入每个膜3,并将该数据用于下次迭代计算过程,即再次执行膜3中的CNSMO子算法对最新送入膜内的数据集进行训练。该迭代过程会反复执行,直到膜4中没有违背KKT条件的样本点。最终系统计算结束,并将此时的分类决策函数作为系统最终计算结果。
算法框架如图6-4:通过在膜内进行反复迭代循环执行该过程,并且对整体数据验证KKT条件,使得该算法相比同类算法能够保留更多的支持向量,可以获得更好的泛化预测能力。最终,得到理想的分类决策函数,算法停止。
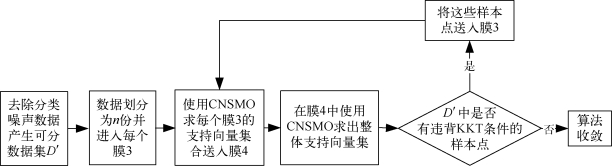
图6-4 PAM-CNSMO算法框架
算法流程如下:

