2.4.2　统一方法

对于具有n个变量和m个子句的SAT问题，构造ΠSAT-uniform（m，n）的统一算法必要资源可以表示如下：

（1）物质的数量：7mn＋2m＋4n＋3；

（2）初始膜的数量：m＋2；

（3）初始物质的数量：2；

（4）规则总数：15mn＋m＋5n＋5。

对于基于促进剂的时间活性膜识别P系统在统一方式下求解SAT问题，与半统一方法一样，系统ΠSAT-uniform（m，n）是时间无关充分的和时间无关完备的。

如果公式γ是可满足的，则在最多10mn＋m＋6n＋4个RS步后，P系统将停止工作；如果公式γ是不满足的，则在最多10mn＋m＋6n－1个RS步之后，P系统将停止工作。对于这两种情况，产生阶段的RS步最多均为10mn＋6n个RS步；对于检测阶段，前者需要m个RS步，后者最多需要m－1个RS步（因为检测阶段的m条规则不可能全部执行）；而对于输出阶段，前者需要4个RS步，后者不需要RS步。显然，系统的整个计算是时间无关多项式有界的。

统一方法与半统一方法相比，半统一方法是对一个具体的例子进行求解，而统一的方法可以解决任意给定大小例子。与文献［12］中构造的P系统相比，本章构造的P系统在证明中没有使用文献［12］中提到的f类规则。此外，基于促进剂的时间活性膜P系统将膜上电荷从三类简化为两类。在本章的工作中，具有较少类型的规则和仅具有两类膜上电荷的P系统仍然可以在多项式RS步内高效地解决SAT问题。

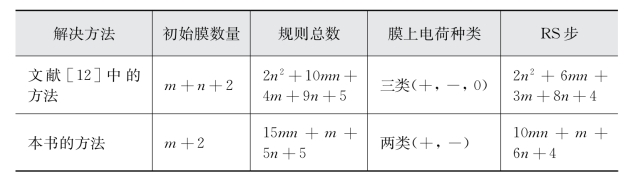
与文献［12］中的时间P系统相比，本文构建的P系统需要更少地计算资源和RS步（见表2-2）。

表2-2　统一方法中计算资源和RS步比较