5.2 HTP-OEP的计算能力以及计算效率
本小节将对基于促进剂和对象进化规则的内稳态类组织膜系统的计算能力和计算效率进行研究。具体地,使用注册机对该系统产生数的通用性进行证明;另外,还将给出该系统(针对标准膜系统)的SAT问题统一解。
5.2.1 HTP-OEP的通用性证明
定理5.1:NOP1((a),(b))HTP-OEP=NRE
证明:下面通过模拟注册机证明HTP-OEP系统的通用性,其中仅针对标准膜系统下HTP-OEP系统的规则类型a和b。NOP n表示系统产生的自然数集合族,其中n表示初始细胞数量。设有通用的带m个注册器的注册机M=(m,H,l 0,l h,I),产生的数存储在注册器1中。另外,假定注册器1中没有加法指令,并且当计算结束时,除注册器1外,其他注册器均为空。系统构造如下:
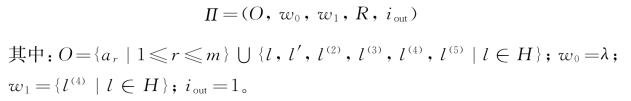
下面将构造规则集合R。
(1)对于每条加法指令l i:(ADD(r),l j,l k),指令集合构造如下:

下面模拟加法指令l i。系统在第一步,通过执行对象进化规则应用规则R 1,对象l i进化为![]() 。第二步,系统非确定性地选择规则R 2或者规则R 3,对象
。第二步,系统非确定性地选择规则R 2或者规则R 3,对象![]() 进化为多重集al j或al k,将会在该细胞中生成一份对象a,使得对象a的数量加1,从而实现了加法指令l i的要求。同时,随机生成了l j或l k,系统开始模拟下一条指令。
进化为多重集al j或al k,将会在该细胞中生成一份对象a,使得对象a的数量加1,从而实现了加法指令l i的要求。同时,随机生成了l j或l k,系统开始模拟下一条指令。
(2)对于每条减法指令l i:(SUB(r),l j,l k),指令集合I构造如下:
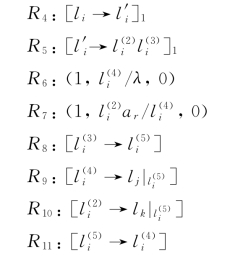
下面开始模拟减法指令l i。系统在某一步,通过应用规则R 4,对象l i进化为![]() ,然后应用规则R 5再进化为多重集
,然后应用规则R 5再进化为多重集![]() 。这时,规则R 6结束执行,对象
。这时,规则R 6结束执行,对象![]() 将出现在环境中。这样,将可能出现以下两种情况:
将出现在环境中。这样,将可能出现以下两种情况:
(1)当对减法指令l i开始模拟时,在细胞1中至少存在一个对象a。在这种情况下,规则R 7和R 8同时执行。这样,在细胞1中就会得到对象![]() 和
和![]() 。因此,在下一个计算步,规则R 9就会开始执行:在促进剂
。因此,在下一个计算步,规则R 9就会开始执行:在促进剂![]() 的作用下,对象
的作用下,对象![]() 进化为l j。同时,通过执行规则R 11,促进剂
进化为l j。同时,通过执行规则R 11,促进剂![]() 消耗后进化为对象
消耗后进化为对象![]() ,以保证下一次模拟中细胞1中存在对象
,以保证下一次模拟中细胞1中存在对象![]() 。这样,系统开始模拟指令l j。
。这样,系统开始模拟指令l j。
(2)当对减法指令l i开始模拟时,在细胞1中没有对象a。在这种情况下,规则R 7不会执行,只执行规则R 8,对象![]() 进化为
进化为![]() 。因此,在下一个计算步,规则R 10就会开始执行:在促进剂
。因此,在下一个计算步,规则R 10就会开始执行:在促进剂![]() 的作用下,对象
的作用下,对象![]() 进化为l k。同时,通过执行规则R 11,促进剂
进化为l k。同时,通过执行规则R 11,促进剂![]() 消耗后进化为对象
消耗后进化为对象![]() ,以保证下一次模拟中细胞1中存在对象
,以保证下一次模拟中细胞1中存在对象![]() 。这样,系统开始模拟指令l k。
。这样,系统开始模拟指令l k。
因此,系统可以正确地模拟M中的加法指令和减法指令。最后,系统将停止计算。这时,对象l h出现在细胞1中。
5.2.2 基于HTP-OEP系统求解SAT问题
定理5.2:SAT问题可以通过一族HTP-OEP系统在线性计算步内以统一的方式解决。
证明:对于具有n个布尔变量和m个子句的公式,本章考虑命题公式γ=C 1∧C 2∧…∧C m,其中,C j=y j,1∨…∨y j,pj,![]() ≤k≤n},1≤j≤m,1≤i≤
≤k≤n},1≤j≤m,1≤i≤![]() 是命题变量x k的否定形式。
是命题变量x k的否定形式。
将例子γ按如下形式编码:
![]()
再通过以下多重集对γ进行编码,其中1≤j≤m,1≤i≤n:

识别内稳态类组织膜系统构造如下:
![]()
其中,O为字母表:
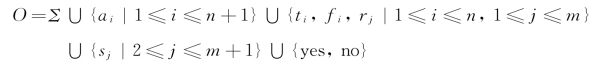
另外,Σ={Y i,j,N i,j|1≤i≤n,1≤j≤m}为在O内的输入字母表;w 0=λ;w 1={yes,no},w 2=a 1是各个细胞内初始物质;i in=2为输入细胞,i out=0是输出区域;R是包含以下规则的规则集。
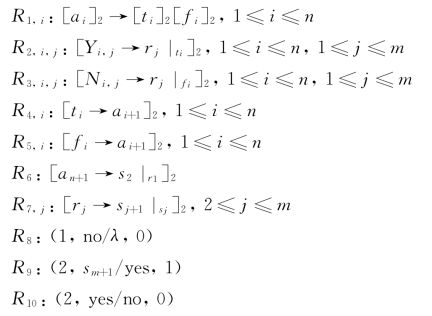 (https://www.daowen.com)
(https://www.daowen.com)
计算过程分为以下几个阶段:
(1)产生阶段:通过分裂规则R 1,i将细胞2分裂成两个新细胞,最终将产生2n个标签为2的细胞;规则R 2,i,j和R 3,i,j用于检查当前变量x i(1≤i≤n)的赋值是否满足每个子句;规则R 4,i和R 5,i主要用于在下一次循环计算过程中应用细胞分裂规则。
(2)检测阶段:系统检查是否存在一组变量的赋值可以满足所有子句。如果存在这样的变量赋值序列,则说明该公式是可满足的;否则说明该公式是不满足的。利用规则R 6和R 7,j,可以检测出所有变量赋值满足的子句,产生最终的检测结果。
(3)输出阶段:通过执行规则R 8、R 9以及R 10,系统根据检测阶段的结果向环境中输出yes或者no作为计算结果。
1)产生阶段
对于给定的含有n个变量和m个子句的布尔公式,设变量为x i,1≤i≤n。通常,细胞2中的对象a i对应于变量x i。系统在初始状态下,细胞1中含有物质yes和no;细胞2中含有对象a 1和输入多重集cod(γ)。
系统在标准膜系统下运行。第一步,系统开始运行,在标签为2的细胞中对象a 1的作用下,应用分裂规则R 1,1将细胞2分裂为两个具有相同标签的新细胞,同时,对象a 1进化为t 1(对应于变量x 1的赋值为真)和f 1(对应于变量x 1的赋值为假)后分别出现在新生成的细胞中。一般地,对象t i和f i分别对应于检查所有子句中变量x i的赋值为真和假是否是可满足的。在第一步,除了应用规则R 1,1之外,规则R 8也开始执行,细胞1中的物质no进入环境中。
当规则R 1,1执行结束时,规则R 2,1,j、R 3,1,j、R 4,1和R 5,1(1≤j≤m)同时开始执行。对于标准膜系统,系统中每条规则的执行时间为一个单位时间。因此,这4个规则是同时完成的。规则R 2,1,j和R 3,1,j用于检查当前变量x i的赋值是否满足每个子句。在促进剂t 1(resp.,f 1)的作用下,如果细胞2中出现对象Y 1,j(resp.,N 1,j),那么规则R 2,1,j(resp.,R 3,1,j)将被应用。如果生成了对象r j,说明当前变量的赋值对应的子句是满足的。由于P系统极大并行性的原理,规则R 2,1,j、R 3,1,j、R 4,1和R 5,1同时开始执行,并且它们在每个细胞2中同时完成执行。
规则R 4,i和R 5,i主要用于在下一次循环计算过程中应用细胞分裂规则。通过使用这两条规则,t 1(resp.,f 1)在作为规则R 2,1,j和R 3,1,j促进剂的同时,也可以作为对象参与到其他规则的具体应用中。这里规则R 4,1和R 5,1将t 1(resp.,f 1)进化为其他对象,即在每个细胞2中生成对象a 2。这样,在下一步中,细胞2又可以进行分裂,从而使以上计算过程不断循环地执行。
当变量x i(1≤i≤n)的第一次循环计算过程结束时,每个细胞2包含一个对象a 2。在对象a 2的影响下,在每个细胞2中同时执行规则R 1,2。通过应用细胞分裂规则,生成标签为2的4个细胞。类似地,该系统以循环的方式执行上述计算过程,所有变量将被赋值并找出满足的子句,直到所有变量的循环计算过程结束执行。
总的来说,系统经过2n步后,产生阶段结束执行,将在每个细胞2中产生对象a n+1。此时,产生2n个标签为2的细胞。
2)检测阶段
当对象a n+1出现在标签为2的细胞中时,每个细胞2中存在着集合{r 1,r 2,…,r m}中的一些对象(或不存在这些对象)。当细胞2中出现对象a n+1,在促进剂r 1(如果该对象存在)作用下,通过使用规则R 6,对象a n+1会进化为s 2。通过应用规则R 7,j,如果一个细胞2中存在着集合{r 1,r 2,…,r m}中的所有对象,那么就可以在细胞2中产生对象s m+1。总的来说,整个检测阶段最多需要m个计算步。
3)输出阶段
当检测阶段结束执行时,将会有以下两种情况。
(1)肯定的答案:公式是可满足的。在这种情况下,在标签为2的细胞中生成对象s m+1,因此可以应用规则R 9,细胞2中就出现了物质yes。下一步,规则R 10开始执行,物质yes被送出细胞2进入环境,而环境中的物质no进入细胞2。因此,当P系统停止工作时,yes将出现在环境中。可以看出,输出阶段需要2个计算步。
(2)否定的答案:公式是不满足的。在这种情况下,对象s m+1不会出现在任何一个标签为2的细胞中。因此,规则R 9和R 10都不会执行。最终,当系统停止工作时,对象no仍然在环境中,由此可以得出没有可满足解的结论。
构造ΠSAT(m,n)的统一算法必要资源可以表示如下:
①物质的数量:2mn+2m+3n+3;
②初始细胞的数量:2;
③初始物质的数量:3;
④规则总数:2mn+m+3n+3;
⑤最大规则长度:2。
最终,系统将在确定的计算步后停止计算,物质yes或no必然会在可行的时间内出现在环境中。因此,系统ΠSAT(m,n)是充分的和完备的。
如果公式γ是可满足的,则在最多m+2n+2个计算步后,P系统将停止工作;如果公式γ是不满足的,则在最多m+2n-1个计算步之后,P系统将停止工作。对于这两种情况,产生阶段的RS步最多均为2n个RS步;对于检测阶段,前者需要m个RS步,后者最多需要m-1个RS步(因为检测阶段的m条规则不可能全部执行);而对于输出阶段,前者需要2个计算步,后者不需要计算步。显然,系统的整个计算是线性有界的。因此,SAT问题可以通过一族内稳态类组织膜系统在线性时间内解决。
定理5.3:SAT∈PMCHTP OEP(2)
推论5.1:NP∪co-NP⊆PMCHTP-OEP(2)
显然,SAT问题属于NP完全问题,在本节给出的识别P系统中,其规则最大长度为2。根据前面的定义以及论述,很容易证明SAT∈PMCHTP-OEP(2),并且SAT∈PMCHTP-OEP(2)在线性时间归约下以及它的补集都是封闭的。
