2.3 基于促进剂的时间活性膜P系统求解SAT问题统一解
定理2.2:SAT问题可以通过一族膜上仅带有两类电荷、使用促进剂的时间活性膜P系统且具有a、b、c、e类规则在多项式RS步内通过膜分裂以统一方式解决。
证明:对于具有n个布尔变量和m个子句的公式,本章考虑命题公式γ=C1∧C2∧…∧Cm,其中,Cj=yj,1∨…∨yj,pj,yj,i∈{xk,![]()
![]() 是命题变量xk的否定形式。考虑多项式时间计算函数为g(n,k)=[(n+k)(n+k+1)/2]+n。
是命题变量xk的否定形式。考虑多项式时间计算函数为g(n,k)=[(n+k)(n+k+1)/2]+n。
将例子γ按如下形式编码:
![]()
再通过以下多重集对γ进行编码,其中1≤j≤m,1≤i≤n。

接下来,定义一族使用促进剂的识别活性膜P系统在时间无关模式下运行,该系统可以处理提供输入多重集cod(γ)的所有例子γ。对于给定的含有n个变量和m个子句的布尔公式,识别P系统构造如下:

(1)产生阶段:
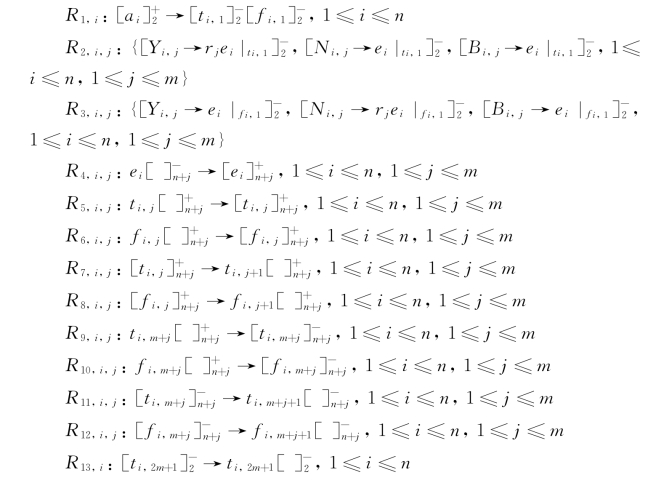
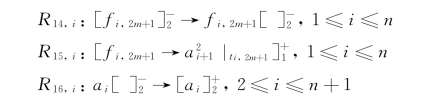
(2)检测阶段:

接下来,将给出系统详细的计算过程。通过该计算过程可以看出,在输入多重集cod(γ)的情况下,基于促进剂的时间活性膜P系统是如何工作的。
1)产生阶段
设e是规则的执行时间。对于给定的含有n个变量和m个子句的布尔公式,设变量为x i,1≤i≤n。一般地,膜2中的对象a i对应于变量x i。系统在初始状态下,膜1中含有对象no;膜2中含有对象a 1和输入多重集cod(γ)。
第一步,系统开始运行,在膜标签为2的膜中对象a 1作用下,应用分裂规则R 1,1将膜2分裂为两个具有相同膜标签的新膜;同时,对象a 1进化为t 1,1和f 1,1后分别出现在新生成的膜中。其中,对象t 1,1对应于变量x 1的赋值为真,对象f 1,1对应于变量x 1的赋值为假。在第一步,除了应用规则R 1,1之外,规则R 19也开始执行。在规则R 1,1和R 19的执行期间,没有任何可以执行的规则,因此这个过程仅需一个RS步。
当规则R 1,1执行结束时,规则R 2,1,j和R 3,1,j(1≤i≤m)同时开始执行。作为促进剂的对象t 1,1和f 1,1分别对应检查所有子句中变量x 1的赋值为真和假是否是可满足的。通过应用规则R 2,1,j和R 3,1,j,在促进剂t i,1(resp.,f i,1)的作用下对象Y 1,j(resp.,N 1,j)进化为对象r j和e 1;其他情况下只能生成对象e 1。对象r j表示对应子句是变量赋值满足的子句。后面用“当前变量”表示每次变量循环计算过程中正在执行的变量,其值对应着取值范围1≤i≤n中的某个值。通常,对于当前变量x i,有m个子句对应于规则R 2,1,j或R 3,1,j中的m条规则。对于规则R 2,1,j或R 3,1,j,需要注意的是,其中包含的所有规则在促进剂的作用下同时开始执行,但每条规则执行时间是任意一个从R到N的不同时间映射,因此它们的完成时间可能不同。该计算过程仅需一个RS步。
当对象e 1出现在膜2中时,规则R 4,1,j开始执行,并且对象e 1进入具有膜标签n+j的任意一个膜,同时将对应膜上电荷从负变为正。由于规则R 2,1,j或R 3,1,j中每条规则的完成时间是不确定的,因此规则R 4,1,j执行结束至多需要2m个RS步。
当膜标签为n+1的膜上电荷变为正时,规则R 5,1,1(resp.,R 6,1,1)开始执行,对象t 1,1(resp.,f 1,1)进入该膜中。然后,通过应用规则R 7,1,1(resp.,R 8,1,1),对象t 1,1(resp.,f 1,1)被送出膜外并且进化为t 1,2(resp.,f 1,2)。接下来,可以应用规则R 5,1,2(resp.,R 6,1,2)。以循环的方式应用规则R 5,1,j(resp.,R 6,1,j)和R 7,1,j(resp.,R 8,1,j),直到对象t 1,m+1(resp.,f 1,m+1)在膜2中产生。当对象t 1,m+1(resp.,f 1,m+1)出现在膜2中时,说明所有规则{R 2,1,j(resp.,R 3,1,j)、R 4,1,j、R 5,1,j(resp.,R 6,1,j)和R 7,1,j(resp.,R 8,1,j)}已经执行结束,此时,规则R 9,1,1(resp.,R 10,1,1)开始执行。从规则R 5,1,1(resp.,R 6,1,1)到R 7,1,m(resp.,R 8,1,m),称为过程一,该过程主要用于检测规则R 2,1,j和R 3,1,j(1≤i≤m)中所有规则是否已经执行结束;而从规则R 9,1,1(resp.,R 10,1,1)到R 11,1,m(resp.,R 12,1,m),称为过程二,该过程主要是用于将膜n+j的膜上电荷重新从正变为负,以便在下一次变量循环的执行过程中可以再次执行规则R 4,i,j。可以看出,过程一和过程二中规则执行过程是类似的。最终,当过程二执行结束时,在膜2中将会产生对象t 1,2m+1(resp.,f 1,2m+1)。此时,对象t 1,2m+1(resp.,f 1,2m+1)被送出膜2外。当对象t 1,2m+1(resp.,f 1,2m+1)出现在膜1中时,说明规则R 13,1(resp.,R 14,1)已经执行结束,然后规则R 15,1开始执行。在促进剂t 1,2m+1的作用下,对象f 1,2m+1进化为两份对象a 2。当对象a 2出现在膜标签为2的膜外时,通过执行规则R 16,2,这些对象进入膜2,同时将该膜上电荷从负变为正。这样,变量x i的第一次循环计算过程执行结束。
当变量x i(1≤i≤n)的第一次循环计算过程执行结束时,每个膜标签为2的膜(即膜2)中包含一份对象a 2。系统开始对变量x 2进行赋值。当规则R 16,3执行结束时,系统继续对变量x 3进行赋值。类似地,每个变量对应的膜持续分裂,得到变量赋值满足的所有子句。对于变量x i的第i次循环,当规则R 13,i和R 14,i执行结束时,通过应用规则R 15,i,对象f i,2m+1进化为两份a i+1。因此,对象a i+1的数量等于膜标签为2的膜的数量。由于系统在时间无关模式下工作,每条规则的执行时间是任意一个从R到N的不同时间映射,因此对象t i,2m+1和f i,2m+1可能不会同时生成。由此可以看出,规则R 15,i具有规则同步功能,因为Σ1≤j≤m{e(R 5,i,j)+e(R 7,i,j)+e(R 9,i,j)+e(R 11,i,j)+e(R 13,i,j)}可能不等于Σ1≤j≤m{e(R 6,i,j)+e(R 8,i,j)+e(R 10,i,j)+e(R 12,i,j)+e(R 14,i,j)}。
总的来说,对于每个包含对象t i,1(resp.,f i,1)的膜,在变量每次循环计算过程中这些膜内应用的规则是相同的,因此每个膜标签为2的膜中对象t i,2m+1(resp.,f i,2m+1)是同时生成的。注意到规则R 4,i,j以非确定性的方式应用,该规则中对应某条规则中的膜标签从n+1到n+m也因此是非确定选择的,但这对后面的计算结果不会有任何影响。
通过应用规则R 16,i,注意到膜标签为2的膜上的电荷从负变为正。因此,该过程只可能有一份对象a i进入一个膜2中。此外,规则R 16,i以极大并行的方式应用于膜标签为2的所有膜,因此在变量的每次循环计算过程中,这条规则的执行都只需要一个RS步。
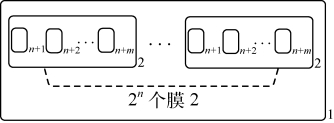
应该指出,该系统以循环的方式执行上述过程,所有变量将被赋值并找出满足的子句,直到所有变量的循环计算过程执行结束。总的来说,在10mn+6n个RS步后,产生阶段将结束执行,这时,会生成2n个膜标签为2的膜,所有这些膜2都将置于膜1中(见图2-2)。
 (https://www.daowen.com)
(https://www.daowen.com)
图2-2 产生阶段结束时的膜结构
2)检测阶段和输出阶段
检测阶段和输出阶段的规则与前面半统一方法中对应的规则是相同的,其执行过程就不再详细说明。总的来说,整个计算过程规则在时间无关模式下运行,检测阶段最多需要m个RS步。
当检测阶段完成时,同样会有以下两种情况:
(1)肯定的答案:CNF公式是可满足的。在这种情况下,在一个膜标签为2的膜中生成对象s m+1,当P系统停止工作时,yes将出现在环境中。总的来说,输出阶段最多需要4个RS步。
(2)否定的答案:CNF公式是不满足的。在这种情况下,对象s m+1不会出现在任何一个膜标签为2的膜中。因此,从R 20到R 23的规则将不会执行。最终,当系统停止时,对象no仍然在环境中,该过程不需要RS步。下面给出一个具体的实例来说明ΠSAT uniform(m,n)是如何工作的,具体的SAT公式为
![]()
系统初始格局如图2-3所示。第一步,膜2在对象a 1的作用下分裂为两个与原始膜标签相同的新膜,同时,对象a 1进化为t 1,1和f 1,1后分别出现在新生成的膜中。在第一步,除了应用规则R 1,1之外,规则R 19也开始执行。在促进剂t 1,1(resp.,f 1,1)的作用下,应用规则R 2,1,j和R 3,1,j(1≤i≤m),对象Y 1,j(resp.,N 1,j)进化为对象r j和e 1;其他情况下只能生成对象e 1。当对象e 1出现在膜2中时,规则R 4,1,j开始执行,并且对象e 1进入具有膜标签4+j的任意一个膜,同时将其膜上电荷从负变为正。不能确定规则R 19的执行是否已经完成,因为这些规则的执行时间长短在时间无关模式下是不确定的。为了方便描述,在后面的图中假设规则R 19已经执行结束。

图2-3 初始格局
当膜标签为5的膜上电荷变为正时,规则R 5,1,j(resp.,R 6,1,j)和R 7,1,j(resp.,R 8,1,j)中包含的所有规则被逐个应用,直到对象t 1,5(resp.,f 1,5)在膜2中生成。接着,规则R 9,1,j(resp.,R 10,1,j)和R 11,1,j(resp.,R 12,1,j)中包含的所有规则被逐个应用,直到对象t 1,9(resp.,f 1,9)在膜2中生成。最后,规则R 15,1开始应用,在促进剂t 1,9的作用下,对象f 1,9进化为两份对象a 2。当对象a 2出现在膜标签为2的膜之外时,规则R 16,2开始应用,对象a 2进入膜2,并将其膜上电荷从负变为正,至此变量的第一次循环计算过程全部完成(见图2-4)。在后面的膜结构图中,有的物质对计算过程以及最后计算结果不会有影响,因此并没有将它们表示在图中。
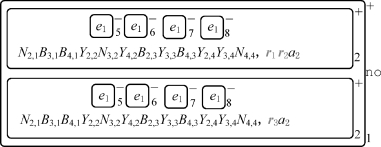
图2-4 变量的第一次循环执行结束后
当变量x i(1≤i≤n)的第一次循环计算过程执行结束,膜标签为2的膜中出现对象a 2。在对象a 2的影响下,规则R 1,2将被应用,生成膜标签为2的4个膜。当变量的第二次循环计算过程中所有规则应用完成的时候,即当规则R 16,3执行结束,可以得到系统此时的格局(见图2-5)。类似地,变量的第三次循环计算过程中所有规则应用完成时,可以得到系统此时的格局(见图2-6);变量的第四次循环计算过程中所有规则应用完成时,可以得到系统此时的格局(见图2-7)。
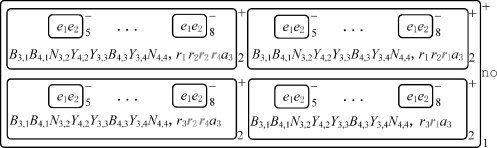
图2-5 变量的第二次循环执行结束后

图2-6 变量的第三次循环执行结束后
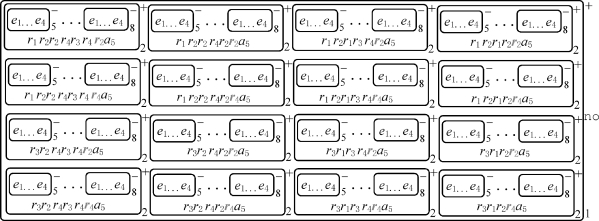
图2-7 变量的第四次循环执行结束后
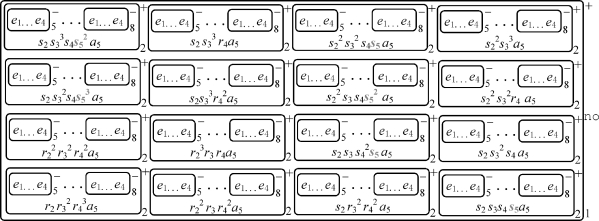
图2-8 检测阶段结束后
当在膜标签为2的膜中产生对象a 5时,如果在膜2中存在对象r 1,则通过使用规则R 17,对象r 1进化为s 2。最后,可以生成对象s 5(参见图2-8)。当对象s 5出现在膜标签为2的膜中时,应用规则R20,在促进剂s5的作用下,对象a5进化为物质yes。最终,物质yes被发送到环境,并且环境中的对象no进入膜1中。当系统停止工作时,yes出现在环境中,说明该CNF公式是可满足的(参见图2-9)。
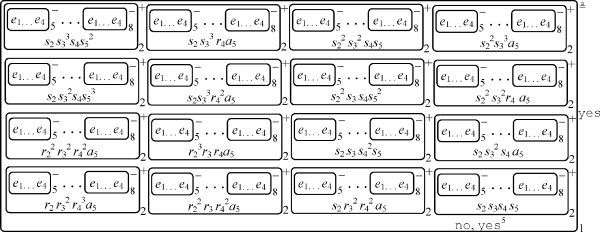
图2-9 系统最终格局
