5.4 HTP-ES/A的计算能力以及计算效率
在本小节,将对基于同向/反向进化规则的内稳态类组织膜系统的计算能力和计算效率进行研究。具体地,通过注册机对该系统产生数的通用性进行证明;另外,还将给出该系统在时间无关模式下的SAT问题统一解。
5.4.1 HTP-ES/A的通用性证明
本节对基于同向/反向进化规则的内稳态类组织膜系统的计算能力进行研究,将该模型与经典的图灵机计算模型进行比较,并在时间无关模式下对该模型产生数的能力进行研究。
定理5.9:![]()
证明:![]() 表示系统产生的自然数集合(m表示初始细胞的数量,n表示系统中的最大规则长度,而f表示系统在时间无关模式下工作)。设有通用的带m个注册器的注册机M=(m,H,l 0,l h,I),产生的数存储在注册器1中。系统构造如下:
表示系统产生的自然数集合(m表示初始细胞的数量,n表示系统中的最大规则长度,而f表示系统在时间无关模式下工作)。设有通用的带m个注册器的注册机M=(m,H,l 0,l h,I),产生的数存储在注册器1中。系统构造如下:
![]()
其中,O={a r|1≤r≤m}∪{l,l′,l(2),l(3),l(4),l(5),l(6)|l∈H};w 0={l(3)|l∈H};w 1=λ;e表示规则执行时间;i out=1。
下面将构造规则集合R。
(1)对于每条加法指令l i:(ADD(r),l j,l k),指令集合构造如下。
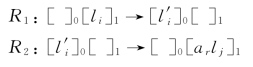
![]()
在某个时刻,系统使用规则R 1模拟ADD指令l i。下一计算步,通过应用R 2或R 3使得注册器r的值增加1,从而满足了ADD指令的要求;另外,产生的对象l j或l k可以模拟下一条指令。显然,ADD指令的结果在时间无关模式下可以正确地模拟。
(2)对于每条减法指令l i:(SUB(r),l j,l k),指令集合I构造如下。
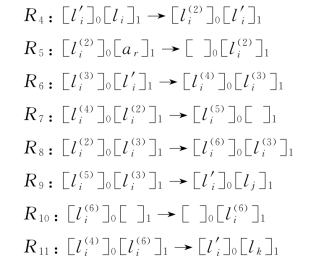
以上构造的规则即使在时间无关模式下也是正确的。首先,系统使用规则R 4开始运行SUB指令l i。下一计算步,会出现以下两种可能性:
(1)第一种情况,至少有一个对象![]() 存在细胞1中。因为存在对象
存在细胞1中。因为存在对象![]() 和
和![]() ,规则R 5和R 6会同时开始执行。接着下一个计算步,规则R 7开始执行,在环境中产生对象
,规则R 5和R 6会同时开始执行。接着下一个计算步,规则R 7开始执行,在环境中产生对象![]() 。然后,执行规则
。然后,执行规则![]() 消耗掉
消耗掉![]() 并产生对象
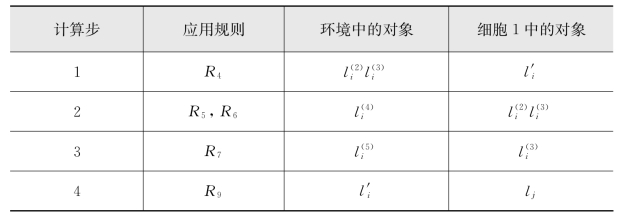
并产生对象![]() 。在这些过程中,注册器r中的值会减1,从而模拟了SUB指令。对于这种情况,规则的执行过程如表5-5(省略环境和细胞1中的部分对象);
。在这些过程中,注册器r中的值会减1,从而模拟了SUB指令。对于这种情况,规则的执行过程如表5-5(省略环境和细胞1中的部分对象);
表5-5 如果对象ar存在
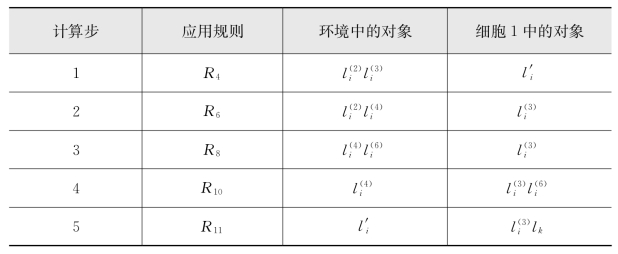
(2)第二种情况,没有对象a r存在细胞1中,显然规则R 5不会执行,接下来,规则R 8、R 10和R 11将依次执行。最终会产生对象l k,说明系统已经准备好了开始模拟指令l k。对于这种情况,规则的执行过程如表5-6所示,表中省略了环境和细胞1中的部分对象。
表5-6 如果对象ar不存在
因此,ADD指令和SUB指令都可以正确地模拟。最终,系统停止计算,此时对象l h会出现在细胞1中。需要说明的是,系统执行的过程和其中规则执行所需的时间是没有关系的。
5.4.2 基于HTP-ES/A系统求解SAT问题
在本节中,使用定义5.3的模型,构造一族识别内稳态类组织膜系统在时间无关模式下求解SAT问题。下面给出具体的证明过程以及通过一个实例阐述该系统的工作过程。
定理5.10:SAT问题可以通过一族HTP-ESA系统在多项式RS步内以统一的方式解决。
证明:对于具有n个布尔变量和m个子句的公式,考虑命题公式γ=C 1∧C 2∧…∧Cm,其中,C j=y j,1∨…∨y j,pj,y j,i∈{x k,-x k|1≤k≤n},1≤j≤m,1≤i≤p j,-x k是命题变量x k的否定形式。
将例子γ按如下形式编码:
![]()
再通过以下多重集对γ进行编码,其中1≤j≤m,1≤i≤n。

接下来,在时间无关模式下定义一族识别HTP-ESA系统:
![]()
其中,O为字母表:
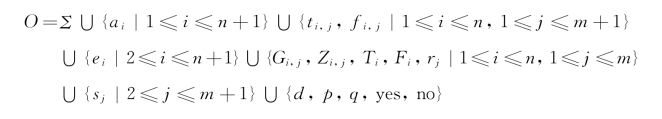
另外,Σ={Y i,j,N i,j,B i,j|1≤i≤n,1≤j≤m};w 0={no,q 2},w 1=p 2,w 2={a 1,d}是各区域的初始物质;i in=1,i out=0;每条规则的执行时间通过时间映射e:R→N得到;R是包含以下规则的规则集。
(1)产生阶段:
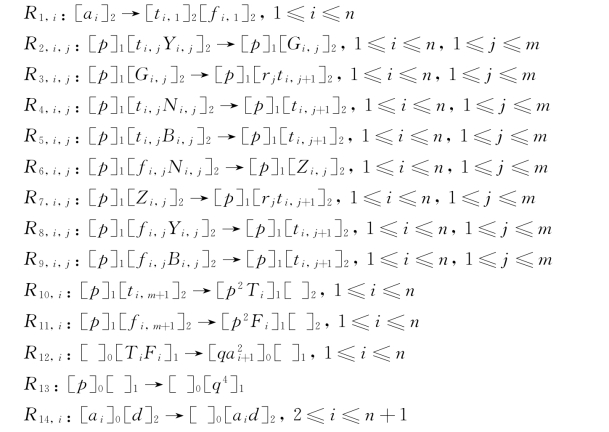
(2)检测阶段:(https://www.daowen.com)
![]()
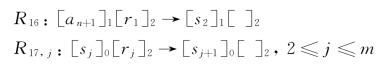
(3)输出阶段:
![]()
1)产生阶段
对象a i对应着SAT公式中的变量x i。系统在第一个RS步,首先执行规则R 1,1,细胞2会分裂为两个具有相同标签的新细胞,同时,对象a 1进化为t 1,1和f 1,1后分别出现在新生成的细胞中。其中,对象t 1,1对应于变量x 1的赋值为真,对象f 1,1对应于变量x 1的赋值为假。当规则R 1,1执行结束时,在下一个RS步,规则从R 2,1,j到R 9,1,j将被选择性地执行。这时,当对象t 1,1和Y 1,1(resp.,f 1,1和N 1,1)出现在细胞2中时,进化反向规则R 2,1,1(resp.,R 6,1,1)会被执行。接下来,通过使用规则R 3,1,j(resp.,R 7,1,j)会被执行,从而在细胞2中产生新的对象r 1。此时,我们可以得出当前的子句对于变量x 1是可满足的。对于其他情况,通过使用对应的规则,那么对象t 1,j(resp.,f 1,j)的下标j值就会增加。然而,由于系统在时间无关模式工作,相应规则的执行时间是无法确定的。因此,需要设计相应的规则用于同步这些规则的执行过程,目的是使得对应的这些计算过程全部完成。最后,对象t 1,j(resp.,f 1,j)的下标j值会达到m+1。这时,从R 10,1到R 14,2的规则会依次执行。这些规则具有以下两个方面的作用:第一是它们可以同步之前的执行规则。这是在时间无关模式下一种非常有效的方法,通过这种规则同步的方法,可以使得不可控的规则执行时间变得相对有序,其中,规则R 12,i就具有规则同步的作用;第二方面是,可以为后续的计算过程产生相应的对象,例如a 2(用于下一次细胞分裂)、p以及q等相关对象。在对变量x 1赋值计算过程的最后时刻,系统在每个细胞标签为2的细胞中产生多重集da 2,其中对象d会在后面规则R 12,2中使用,而对象a 2用于下一次分裂规则R 1,2(准备进入下一次变量的循环过程)。
接下来的计算过程和前面对变量x 1的计算过程是类似的,也就是说后面的计算过程是以循环的方式不断地对所有的变量进行赋值并找出可满足的情况。当对应于n的变量赋值完成时,产生阶段也就结束。总的来讲,经过3mn+7n个RS步后,产生阶段将结束执行。此时,生成2n个标签为2的细胞。
2)检测阶段
当对象a n+1出现在标签为2的细胞中时,说明产生阶段所有规则已经执行结束。这个时刻,每个细胞2中存在着集合{r 1,r 2,…,r m}中的一些对象(或不存在这些对象),当一个细胞中出现这个集合中的所有元素时,说明该SAT问题是可满足的;否则,就说明该SAT问题是不可满足的。因此,检测阶段的这三条规则就是检查是否存在一个标签为2的细胞中包含集合{r 1,r 2,…,r m}中的所有元素。
3)输出阶段
一旦在细胞2中产生s m+1,规则R 18就会开始应用。最终,系统停止计算,yes出现在输出区域,则说明该SAT问题有可满足解;相反,如果对象s m+1没有出现,no继续保留在输出区域,则说明该SAT问题没有可满足解。下面给出一个如下的实例来说明ΠSAT(m,n)是如何工作的,具体的SAT问题使用公式为![]() 。
。
对于该公式,m=n=3。ΠSAT(m,n)的初始格局如图5-6所示。第一步,使用细胞分裂规则使得细胞2的数量得以增加。然后,规则从R 2,1,j到R 9,1,j将被选择性地执行,生成t 1,4(resp.,f 1,4)。当规则R 14,1执行完成,对象a 2会出现在所有标签为2的细胞中,从而完成了变量x i的第一次循环过程。这个时刻,可以得到此时的配置(如图5-7所示)。
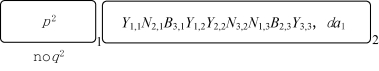
图5-6 初始格局
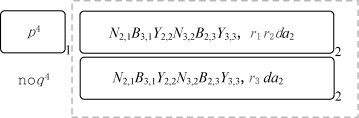
图5-7 变量的第一次循环执行结束后
在完成了变量x i的第一次循环过程以后,因为环境中存在对象a 2,以及细胞2中存在对象d,通过使用进化反向规则R 14,2,每个环境中的对象a 2会进入每个标签为2的细胞中。通过这种方式,a 2的出现会开始变量x 2的循环过程。接下来,变量x 2和x 1的执行过程是类似的。当变量x 2执行结束,可以得到系统此时的格局(参见图5-8)。类似地,当变量x 3执行结束,可以得到系统此时的格局(参见图5-9)。
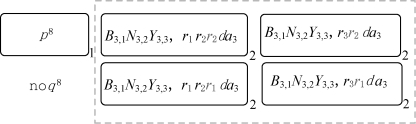
图5-8 变量的第二次循环执行结束后
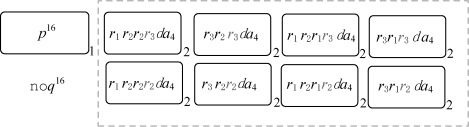
图5-9 变量的第三次循环执行结束后
当在标签为2的细胞中产生对象a 4时,系统进入检测阶段。通过使用这个阶段的规则可以生成对象s 4,得到此时的配置(如图5-10所示)。
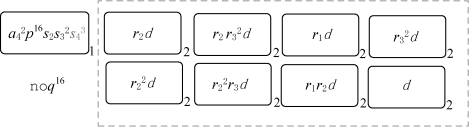
图5-10 检测阶段结束后
最终,系统会在确定的RS步以后停止计算,并在输出区域产生计算结果。当对象s 4出现在细胞1中时,应用规则R 18,对象yes将出现在环境中。此时系统停止计算,可以得出该公式是可满足的(参见图5-11)。
对于以上计算过程,所需计算资源列出如下。
(1)物质的数量:6mn+3n+m+6;
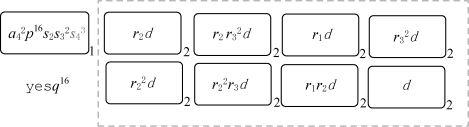
图5-11 系统最终格局
(2)初始细胞的数量:5;
(3)初始物质的数量:2;
(4)规则总数:8mn+4n+m+5;
(5)规则的最大长度:5。
系统停止计算时,如果物质yes在输出细胞中,则公式γ是可满足的。产生阶段需要3mn+7n个RS步。如果公式γ是可满足的,则检测阶段和输出阶段最多分别需要m个和2个RS步;如果公式γ是不可满足的,则检测阶段和输出阶段最多分别需要m-1个和0个RS步。
定理5.11:SAT∈![]()
推论5.3:NP∪co-NP⊆![]()
本章提出了一种基于生物内稳态的类组织膜系统变体,去除了“环境中对象数量为无穷多”这个假设,分别建立三个内稳态类组织膜系统,使系统处于“内稳态”状态。然后分别研究了这三个系统的计算能力以及计算效率。结果表明,这三类模型作为产生数的计算设备,它们的计算能力与图灵机等价;另外,在求解NP完全问题中具有较好的计算效率,该方法也可用于图论中其他类似问题的求解,例如哈密尔顿路径问题、顶点覆盖问题、最大团问题等。
本章研究的膜系统都是在极大并行模式下运行的[14]。最近,有研究提出了一种新的运行模式——FLAT极大并行模式[15],在该模式下内稳态类组织膜系统的计算性能还有待进一步研究。另外,还可以考虑在其他运行模式下工作,例如极小并行模式[16]、局部同步模式[17]等。
