6.1 基于分类噪声检测的序列最小优化算法
本节从SVM的基本模型出发，介绍了使用相对密度检测分类噪声数据的CNSMO方法。
6.1.1 SVM基本模型
SVM原始模型是凸二次规划模型，容易通过梯度下降等传统方法获得全局最优解，所以在线性程度较好及小样本数据下集中体现了良好的泛化能力。SVM的原始线性模型通过引入核函数和核内积的方式来产生非线性模型，核内积避开了对高维映射特征的具体计算，从而避免了“维度灾难”的问题。SVM的核心思想是通过最大化两类样本间隔来获得最优决策超平面。如图6-1，实际应用的数据集中一般都含有一定的噪声数据，因此并不是完全可分的。
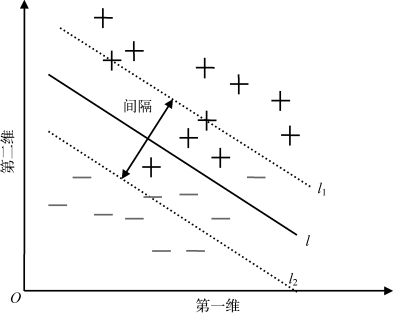
图6-1 线性不可分分类示意图
对于样本集｛（x i，y i）｝，其中，x i∈R n，y i∈｛＋1，－1｝，i＝1，…，l。若存在w∈R n，b∈R和正数ε，y i（ωi·x＋b）≥1，i＝1，…，l，SVM处理不可分数据集的原始模型表示如下：
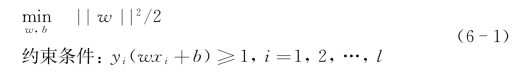
通过引入惩罚系数C，转化为如下表达式：
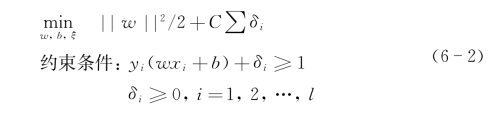
其中，w为决策平面的法向量，l为训练集中的样本数，δi表示每个错误划分样本到决策曲面的距离，C可以刻画目标函数对错误划分样本的容纳权重。由此，线性硬间隔SVM转化为线性软间隔SVM。通过对偶化处理并进一步引入核函数k（x i，x j），其对偶非线性模型转化成如下表达式：
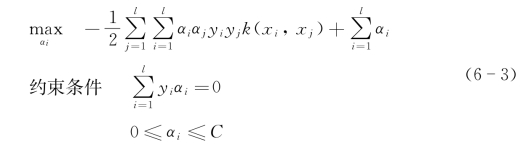
设
为模型式（6-3）的最优解，决策超平面的法向量为
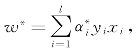决策函数中的偏置可使用支持向量计算，为y j－〈w，x j〉，j∈｛j|0＜
＜C｝，决策函数为f（x）＝sgn（w*x＋b*）。
6.1.2 基于分类噪声检测的CNSMO
SVM在处理非线性数据集中，核函数可能会过度映射而导致过拟合现象。过拟合现象的重要原因在于对非噪声数据进行了不合理划分，从而使决策函数的预测能力快速下降。这种由过度映射带来的过拟合现象使得SVM在核参数的优化和核函数的选择方面变得相对困难。现有的SVM算法在训练过程中都需要交叉验证来避免过拟合，以保证算法的泛化能力。而交叉验证会产生过多的中间分类器，使得算法的训练时间较长。为了解决该问题，文献［15］首次提出了分类噪声的方法，从而避免了使用交叉验证。本章采用相对密度的方法提前检测出分类噪声数据［1518］，在训练数据集中去除噪声点后再进行训练，避免了使用交叉验证，从而加快最优分类器的参数优化过程，显著减少分类器学习过程中的训练时间。
定义6.1：绝对密度［15］
给定数据集D∈R d，对任一个样本点p∈D和q∈D，其中d（p，q）表示点p和点q之间的距离。p的k最近邻表示为N k（p），其中N k（p）＝｛q∈D|d（p，q）≤k-distance（p）｝。p的绝对密度表示为Absolute Density（p，D）＝k／∑d（p，q），for q∈N k（p）。
定义6.2：相对密度［15］
给定数据集D∈R d，D中包含D＋以及D－两类样本集合，对于任意一个样本点o∈D＋，其相对密度为
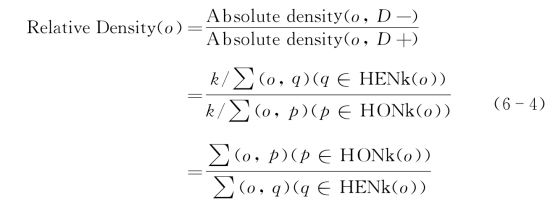
根据式（6-4），可以计算出某个样本点是否为分类噪声。如果式（6-4）的值大于1，则可以判断出该样本点为分类噪声。
序列最小优化（sequential minimal optimization，SMO）算法是应用最为广泛的支持向量机分解算法，该算法每次更新的样本数为2。其通过不同迭代更新每对样本来不断逼近最终的决策超平面。虽然迭代次数较多，但是其迭代模型变成了解析的形式，因此，整体的收敛速度相对于其他大多数分解算法反而更快。CNSMO算法进一步通过排除分类噪声来优化SMO算法［19］。
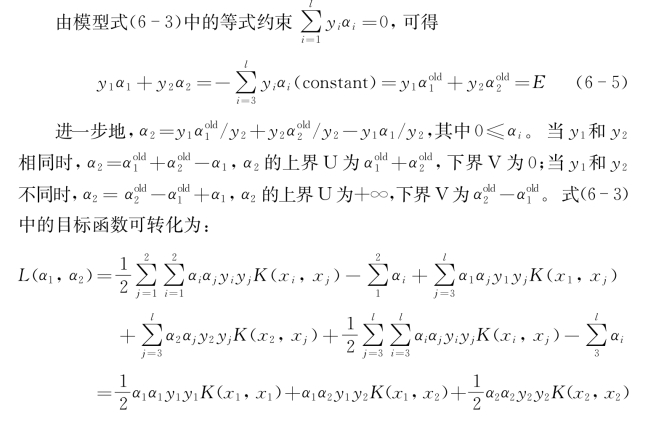
其中f（x）为迭代过程中由原拉格朗日系数所决定的决策函数。
结合拉格朗日系数的上下界，获得如下的迭代更新方程：
