3.1.1　马尔可夫模型

3.1.1　马尔可夫模型

存在一类重要的随机过程:如果一个系统有N个　状态S1,S2,…,SN,随着时间的推移,该系统从某一状态转移到另一状态。如果用qt表示系统在时间t的状态变量,那么,t时刻的状态取值为Sj(1≤j≤N)的概率取决于前t－1个时刻(1,2,…,t－1)的状态,该概率为:P(qt＝Sj｜qt－1＝Si,qt－2＝Sk,…)。

假设1　如果在特定情况下,系统在时间t的状态只与其在时间t－1的状态相关,则该系统构成一个离散的一阶马尔柯夫链:

假设2　如果只考虑公式(3.1)独立于时间t的随机过程,即所谓的不动性假设,状态与时间无关,那么:

该随机过程称为马尔柯夫模型(Markov Model)。

在马尔柯夫模型中,状态团概率必须满足下列条件:

马尔柯夫模型又可视为随机有限状态自动机,该有限状态自动机的每一个状态转换过程都有一个相应的概率,该概率表示自动机采用这一状态转换的可能性。马尔柯夫链可以表示成状态图(转移弧上有概率的非确定的有限状态自动机),零概率的转移弧省略,每个节点上所有发出弧的概率之和等于1。具体见图3.1。

状态序列S1,S2,…,ST的概率:

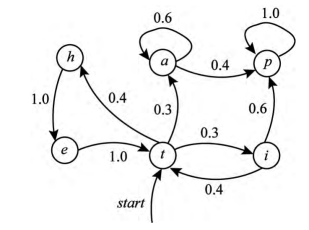
图3.1　Markov Model的状态转移示例

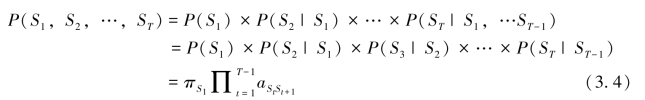
其中,πi＝P(q1＝Si)为初始状态的概率。

如:P(t,i,p)＝P(S1＝t)×P(S2＝i｜S1＝t)×P(S3＝p｜S2＝i)

＝1.0×0.3×0.6＝0.18