3.1.3　Forward-Backword算法

3.1.3　Forward-Backword算法

对于给定的HMM模型λ＝(A,B,π)和观察序列O＝{o1,…,oT},计算出现当前的观测的概率P(O｜λ)。记Q＝{q1,…,qT},则利用条件概率的性质容易计算:

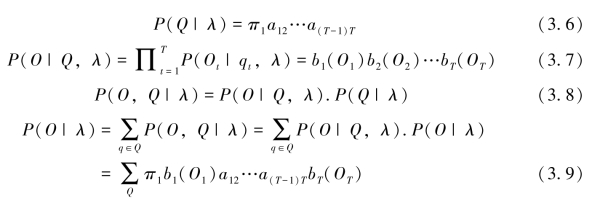
该方法计算量太大,其复杂度为O(2 T NT),如当观测序列较长及状态数量多时,其计算不可行,因此必须研究简化计算方法。很多学者研究了此问题,其中最知名的为前向-后向算法^[6],其详细描述如表3.1和表3.2所示。

表3.1　前向算法

表3.2　后向算法

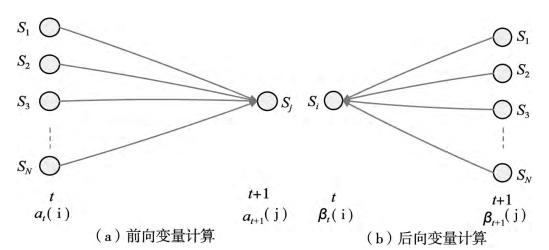
递推计算是前向变量计算的主要部分,如图3.3所示,计算αt＋1(j),需考虑所有可能在t＋1时刻转移到sj的t时刻所处的状态。

图3.3　前后向变量计算过程示意

使用前向算法的复杂度是O(N2T),其精确的计算复杂度是N(N＋1)(T－1)＋N次乘法运算和N(N＋1)(T－1)次加法运算。而不是基本算法的复杂度O(2TNT)那样大。例如当N＝5,T＝100时,用前向算法计算量大约是3000,而直接计算P(O｜λ)的方法的计算量约是1072,约放大了69个数量级。

与此类似,我们也可用后向算法对P(O｜λ)进行计算。引入一个后向变量βt(i)定义如下:

表示观察序列Ot＋1Ot＋2…OT在t时刻处于状态Si的概率。

后向变量计算的复杂度也是O(N2T)。

可以将前后向算法结合起来较方便的计算P(O｜λ):