5.1.1 博弈模型要素和基本概念
在使用博弈论进行分析之前,有必要对博弈论中出现的基本术语进行简单的说明。博弈论的基本术语包括:参与人、行动、策略、信息、支付函数(收益)、结果和均衡[9]。其中参与人、策略和支付函数是描述一个博弈所需要的最基本的要素。
(l)参与人(Player)指的是一个博弈中的决策主体,他的目的是通过选择行为以最大化自己的支付(受益),参与人可以是自然、个体,也可以是团体,如企业、国家。博弈模型中要求参与人是“理性”的。所谓“理性”,一般不是指道德标准。从参加博弈的参与人的眼光来看,他们试图去实施自己认为可能最好的行为,尽管这种行为有可能损害了其他的参与人。因此“理性行为”似乎有点“利己,不管是否损人”。从博弈分析人员的“旁观”眼光来看一般不会去擅自判断参与人的动机究竟如何。由于参与人的相互依存性,博弈中一个理性的决策必定建立在预测其他参与人的反应之上。一个参与人将自己置身于其他参与人的位置并为他着想从而预测其他参与人将选择的行动,在这个基础上该参与人决定自己最理想的行动,这就是博弈论方法的本质和精髓。所以,参与人应该清楚地知道自己的目标和利益所在,在博弈中总是采取最佳策略以实现其效用和利益的最大化。
(2)行动(Action)是指参与人在博弈的某个时点的决策变量。一般地用ai表示第i个参与人的一个特定行动,A＝{ai}表示可供i选择的所有行动的集合。
(3)策略(Strategies)是指参与人选择其行为的规则,也就是指参与人应该在什么条件下选择什么样的行动,以保证自身利益最大化。
(4)信息(Information)是指参与人在博弈过程中的知识,特别是有关其他参与人(对手)的特征和行动的知识。即该参与人所掌握的其他参与人的、对其决策有影响的所有知识。
(5)支付函数(Payoff Function)当所有的参与人采取的策略确定后,他们就有各自的“支付函数”,或者称“盈利函数”。支付函数表达了参与人从博弈中能够得到的收益或支付水平,它是所有参与人策略的函数。不同的策略可能导致不同的收益,是每个参与人真正关心的东西。
博弈论中的每一个参与人作出理性决策的重要依据之一是他的可能盈利有多少,这就是一个参与人需要认真计算的盈利函数。对于每一个参与人,如果他们在可供自己选择的策略空间中任取一策略作为自己的行动,既不会给自己带来盈利,又不会使他们必须付出,这种失去了激励机制的游戏本身也就失去了“博”的意义,在社会经济领域中尤其不太可能出现这类现象。盈利函数的结构与取值无疑将会影响到参与人的行为,因而也影响到了博弈的最终结局。
由此,盈利函数的确定在博弈论研究中是件非常重要的事情。从对博弈的不同角度考虑,从参与人不同的观点出发可以有形形色色的盈利函数,并不唯一。
(6)结果(Outcome)是指博弈分析者感兴趣的要素集合。如均衡策略组合,均衡行动组合,均衡支付组合。
(7)均衡(Equilibrium)是指所有参与人的最优策略的组合。均衡实际上就是博弈模型的解。
纳什(John Nash)在1950年[10]和1951[11]年发表了两篇关于非合作博弈的重要文章,在非常一般的意义上定义了非合作博弈及其均衡解,并证明了均衡解的存在,基本上奠定了现代非合作博弈论的基石。
纳什均衡是指由所有参与者的最优策略组成的策略组合。在这种策略组合中,给定其他参与者的策略,没有任何单个参与者有积极性选择其他策略,也就没有人主动去打破这种均衡;相反,一种均衡或制度安排,如果不是一种纳什均衡,即不是所有参与者的最优策略组合,就不能成立或者至少不能持续。这就是纳什均衡的哲学思想。
下面给出本章中所涉及的相关概念的形式定义。
定义5.1 博弈的战略式表述。博弈的战略式表述含有以下三个要素:(1)博弈参与者集合i∈Γ,Γ＝{1,2,…,n};每个参与者的战略空间Si,i＝1,2,…,n;每个参与者的收益函数ui(s1,s2,…,si,…,sn),i＝1,2,…,n。在一个有n个参与者的博弈中,参与者的战略空间为S1,S2,…,Sn,收益函数为u1,u2,…,un,标准式用G＝{S1,…,Sn;u1,…,un}表示此博弈。
定义5.2 纳什(Nash)均衡。在n个参与者标准式博弈G＝{S1,…,Sn;u1,…,un}中,如果对于每一个参与者i(i＝1,2,…,n),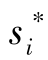
是针对其他n－1个参与者所选战略
的最优反应战略,即:
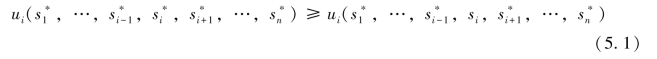
对Si中所有的si都成立,即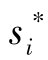
是取优化问题
的解,则战略组合
称为博弈的一个纳什均衡。如果一个战略组合
不是纳什均衡,那么至少有一个参与者有动因偏离这个结果。
定义5.3 混合战略。对标准式博弈G＝{S1,…,Sn;u1,…,un},假设Si＝{si1,si2,…,siK},那么参与者i的一个混合战略是概率分布pi＝(pi1,pi2,…,piK),其中,对所有k＝1,2,…,K都有0≤pik≤1且
用Pi表示参与者i的混合战略空间,应有pi∈Pi,用p＝{p1,p2,…,pn}表示一种混合战略组合。用P＝×Pi表示混合空间组合(即Pi的乘积空间),应有p∈P。
定义5.4 期望收益函数。设p＝(p1,…,pi,…,pn)是一个混合战略组合,其中,pi＝(pi1,pi2,…,piK)是Si＝{si1,si2,…,siK}的一个概率分布。ui(s)＝ui(s1,…,sn)是参与者i的收益函数,参与者i的期望收益函数可定义为:这里s＝(s1,s2,…,sn)是一个特定的战略组合,对应这一战略组合,参与者i的收益是ui(s)＝ui(s1,…,sn),p1(s1).p2(s2)…pn(sn)是出现战略组合s＝(s1,s2,…,sn)的联合概率,求和是对战略空间组合S＝×Si中所有可能的战略组合s进行的。
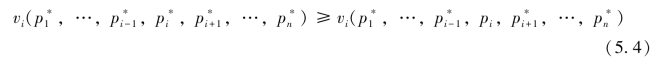
定义5.5 混合战略纳什均衡。在n个参与者标准式博弈G＝{S1,…,Sn;u1,…,un}中,如果对于每一个参与者i(i＝1,2,…,n),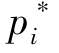
是针对其他n－1个参与者所选混合战略组合
的最优反应,即:对Pi中所有pi都成立,则混合战略组合p*＝
是一个纳什均衡。定义表明,参与者i的最优反应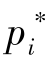
是最优化问题:的解。
定理5.1 纳什均衡的存在性定理I(Nash,1950)。在n个参与者的战略式博弈G＝{S1,…,Sn;u1,…,un}中,如果n是有限的且对每个参与者i的战略空间Si中的战略si是有限的,则博弈至少存在一个纳什均衡(纯战略的或混合战略的)。