4.2.2 HSMM中状态驻留时间讨论
传统HMM模型最主要的不足在于其关于系统在某一状态的持续时间的假设。马尔可夫链隐含了这样一个事实:在系统处于状态Si时,若其状态转移到自身的概率为aii,则系统在状态Si持续时间d的概率密度pi(d)为:pi(d)＝(aii)d－1(1－aii),即呈指数分布。而在现实世界中作如此假设,对某些问题并不合适。HMM的系统状态转移过程如图4.3所示。
HMM中系统在状态Si持续时间d的概率密度pi(d)计算方法如下:
设观测序列为:O＝
则:P(O｜Model,q1＝Si)＝(aii)d－1(1－aii)＝pi(d)
驻留时间的期望值为: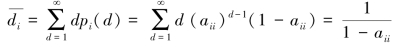
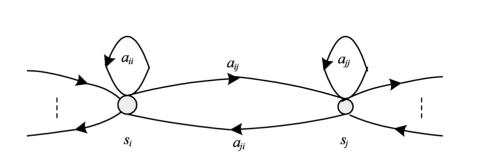
图4.3 HMM状态转移图
例4.1 一个三状态Markov过程转移矩阵如下所示,求系统在三个状态的驻留时间的期望值。
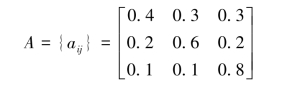
解:系统在三个状态的持续时间的期望值可计算如下:
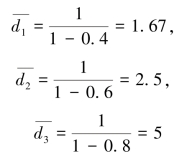
马尔可夫过程同样满足指数分布的“无记忆性”特性(Memory Less Property,又称遗失记忆性),即表示如果一个随机变量呈指数分布,它的条件概率遵循:P(di＞s＋t｜di＞s)＝P(di＞t)for all s,t≥0。
证明:
由上述的概率密度函数知马尔可夫过程状态分布函数为:
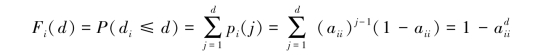
而
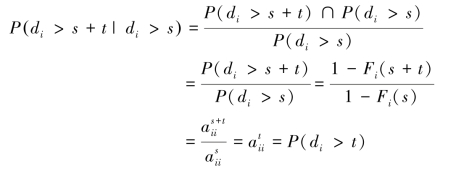
即该函数满足:P(di＞s＋t｜di＞s)＝P(di＞t)。
上述结论说明系统在任意状态i上的驻留时间d具有无记忆性,即已知系统在状态i上驻留了s个单位时间后,再在状态i上驻留t个时间单位的概率与系统从进入i状态起在状态i上驻留t个时间单位的概率相同。此结论与网络安全态势评估中系统状态驻留时间的分布情况有一定出入。因此我们考虑利用HSMM模型来对网络安全防范系统进行建模。HSMM模型有如下优点:HSMM将任意状态qi分成d(di＝1,2,3,…,D)个子状态
系统每次进入状态qi时di的取值可能不同,其分布规律与pi(d)有关,每个子状态的统计特征(指产生不同观察值的分布特征)与父状态qi的统计特征相同,每个子状态产生一个观察值,于是状态qi共产生di个观察值,然后进入下一个状态,重复上一过程,这样就构成了一个HSMM。因此HSMM具有很好的层次化结构。而状态驻留时间D本质上代表了检测数据时间上的持续性。因此,可以想象,如果主机遭受异常,在数学模型上参数D可以有所反映。所以,可以考虑在状态驻留时间D未知的情况下,通过训练好的HSMM模型来对参数D进行估计,以确定攻击发生的大致时间。
HSMM的系统状态转移过程如图4.4所示。
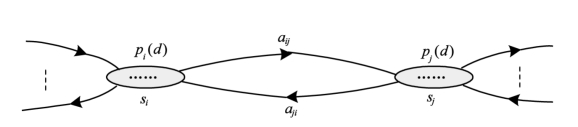
图4.4 HSMM状态转移图
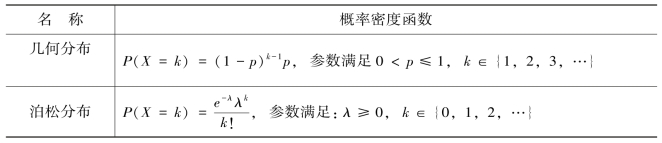
在本章中我们对系统状态驻留时间的分布进行扩充研究,对pi(d)分别为对数分布、负二项分布、几何分布和泊松分布[8]的情况下对系统的安全态势进行评测。各种概率分布的密度函数如表4.7所示。
表4.7 系统状态驻留时间概率分布
续表
