4.1.6　改进的Baum-Welch算法

同HMM一样,HSMM的Baum-Welch算法也是主要解决问题3,即模型训练及参数重估问题。实际上也是极大似然准则的一个应用,它采用了一种多次迭代的优化算法,用Lagrange数乘法构造一个目标函数Q,其中包含了所有HSMM参数作为变量,然后令Q对各个变量的偏倒数为0,推导出Q达到极点时新的HSMM参数相对于旧模型参数之间的关系,从而得到HSMM各参数的估计,用新旧HSMM模型参数之间的函数关系反复迭代运算,直到HSMM模型参数不再发生明显的变化为止。

结合广义前向和广义后向变量,Keiichiro Oura^[6][7]等人推导出了HSMM各个参数的重估公式。为节约篇幅,在此不再赘述。

同HMM类似,HSMM参数λ＝(π,A,B,pj(d))的求取过程为:根据观察值序列O和选取的初始模型λ0＝(π0,A0,B0,pj(d)0),由重估公式,求得一组新参数亦即得到了一个新的模型,可以证明,由重估公式得到的比λ0＝(π0,A0,B0,pj(d)0)在表示观察值序列O方面要好。那么,重复这个过程,逐步改进模型参数,直到P(O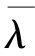｜)收敛,即不再明显增大,此时的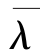即为所求的模型参数。