3.1.2 隐马尔可夫模型
HMM是一个双重随机过程,其中之一是隐蔽的(不可观测的)具有有限状态的Markov链,另一个是与Markov链的每一状态相关联的观察事件的随机过程(可观测的)。隐蔽Markov链的特征要靠可观测到的信号特征揭示。
隐蔽Markov链某一时刻的状态概率分布由对应的状态观察事件的随机过程描述,而其随时间的变化则由隐蔽Markov链的转移概率描述。从观察者的角度看,只有观察值是可见的,不像Markov链模型中的观察值和状态一一对应。由于状态不可见,只能通过一个可观察的随机过程去感知状态的存在及其特性,因而称之为“隐”Markov模型。HMM可用来估计隐藏于表面事件背后的状态的概率。HMM模型如图3.2所示。
HMM描述的随机过程除了要满足马尔可夫模型的两个假设外,还要满足第三个假设:
假设3 观测序列满足输出独立性,即观测值只与当前状态有关
HMM模型可以用五元组λ＝(S,V,A,B,π)表示:
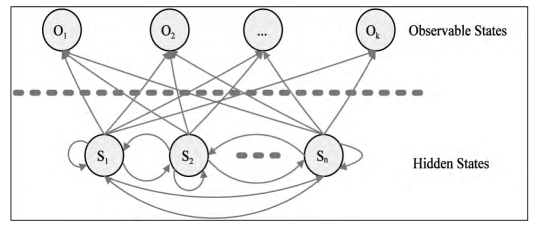
图3.2 Hidden Markov Model
S:模型中的(隐藏)状态,设有N个状态S1,…,SN,则在t时刻所处的状态为qt,qt∈S＝{S1,…,SN}。
V:可观察状态集,设有M个观测状态,则V＝{v1,…,vM},任一观测序列可记为O＝{o1,…,oT},ot∈V,观测序列的长度为T。
A:状态转移矩阵,A＝aij,aij＝P(qt＝Sj｜qt－1＝Si),1≤i,j≤N,aij≥0,
B:观测矩阵,从状态Sj观察到某一特定可观察符号vk的概率分布矩阵:B＝bj(k),bj(k)＝P(Ot＝vk｜qt＝Sj),1≤j≤N,1≤k≤M,bj(k)≥0,
π:初始状态的概率分布,π＝πi,其中πi＝P(q1＝Si),1≤i≤N,πi≥0,
通常将HMM简记为λ＝(A,B,π)。
在应用中研究隐Markov的主要方面有:
(1)学习问题:从一个观测序列O＝{o1,…,oT}出发,估计模型参数组λ＝(A,B,π),称为学习问题,也就是参数估计问题。
(2)解码问题:从一观测序列O＝{o1,…,oT}及已知模型λ＝(A,B,π)出发,估计状态Sn的最佳值,称为解码问题,这是状态估计问题。
(3)识别问题:对于一个特定的观测链O＝{o1,…,oT},已知它可能是由已经学习好的若干模型之一所得的观测,要决定此观测究竟是行自其中哪一个模型,这称为识别问题,就是分类问题。