4.1.1 HSMM定义
HSMM是在对离散HMM和连续HMM思想进行综合后提出来的,最早由Huang[1]等人提出并进行了系统研究,之后Bellgarda和Nabamoo[2]也独立地提出了这一思想。
HSMM修改了HMM模型关于系统在某个状态的驻留时间服从指数分布的假定,更适合于描述计算机系统运行的实际情况。马尔可夫链是状态和时间参数都离散的马尔可夫过程,可用于描述随机过程统计特性的概率模型。这里所说的随机过程,一般都是有限长的随机序列,它是一个双重随机过程,其中之一是Markov链,描述状态之间的转移。另一个随机过程是描述状态和观测变量之间的统计对应关系。HSMM模型如图4.1所示。
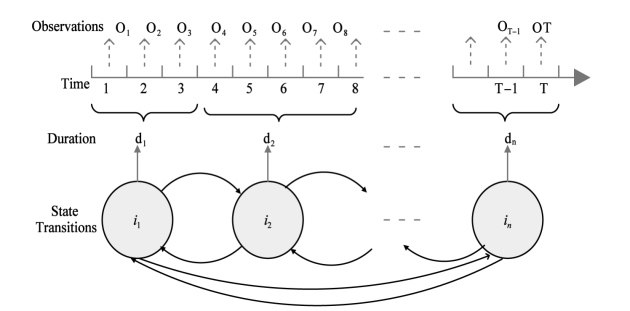
图4.1 HSMM模型
定义4.1 隐半马尔可夫模型(Hidden Semi-Marlov Model,简记为HSMM)一个有N个状态的HSMM是由六元组参数λ={N,M,A,B,π,Pj(d)}表示,它是一种可用于描述一种随机序列统计特性的概率模型,其中各参数意义如下[3]。
(1)N,模型的状态数目。
(2)M,可观测的符号数目。
(3)π={π1,π2,…,πN},为状态初始概率分布。用于描述观测序列O在t=1时刻所处状态q属于模型中各状态的概率分布,即:πi=P(q1=Si),i=1,2,…,N,式中N表示状态数目。(https://www.daowen.com)
(4)A={aij}为状态转移概率矩阵,满足0≤aij≤1,1≤i,j≤N,对于一阶HSMM,当前所处状态qt只与qt-1有关,即:aij=P(qt=Sj|qt-1=Si)。
(5)B={bj(k)}为状态Sj的观测符号的概率,它是随机变量或随机矢量在各状态的观察概率空间中的分布。bj(k)=P(ot=vk|qt=Sj),式中qt表示半马尔可夫链在时间t时的状态,t=1,2,…,T,ot为相应的观测值。
(6)pj(d)为状态持续时间密度函数,即状态Sj持续d个时间单元的概率。d∈{1,2,…,D},D为最大的状态持续时间单元。
对于给定的HSMM,为了在实际中能够更好地进行应用,需要解决3个基本问题[4]。
问题1:HSMM的概率推理问题(广义前向-后向算法)。给定观察序列O1O2…OT和模型λ,考虑如何有效地计算观察向量序列在给定模型下的概率P(O|λ)。
问题2:HSMM的解码问题(改进Viterbi算法)。给定观察向量序列O1O2…OT和模型λ,考虑如何选择一个相应的状态序列q={q1,q2,…},能够在某种意义上达到最优。
问题3:HSMM的训练问题(改进Baum-Welch算法)。给定观察向量序列O1O2…OT,如何调整模型参数,使P(O|λ))为更大,即模型的训练问题。
