4.1.3 改进的Forward-Backward算法
2026年01月15日
4.1.3 改进的Forward-Backward算法
为表述方便引入符号τt表示系统处于状态qt的持续时间,用二元组(qt,τt)的取值为(si,d)时表示此半马尔可夫链将会在状态si上保持时间为t+1-d,在t+d处,会转为下一个系统状态,其中1≤d。另将观察序列片断记为![]() oa+1,…,ob},1≤a<b≤T。
oa+1,…,ob},1≤a<b≤T。
定义前向变量为αt(i,d)=P(ot1,(qt,τt)=(si,d)|λ),状态(qt,τt)=(si,d)由状态(qt-1,τt-1)=(si,d+1)或(qt-1,τt-1)=(sj,1),j≠i转移而来。因此可以得到下述递推公式:αt(i,d)=αt-1(i,d+1)bi(ot)+![]() i))bi(ot)pi(d),1≤d。初始条件为α1(i,d)=πi.bi(o1).pi(d)。最后可计算观察序列O的条件概率为:P(O|λ)=
i))bi(ot)pi(d),1≤d。初始条件为α1(i,d)=πi.bi(o1).pi(d)。最后可计算观察序列O的条件概率为:P(O|λ)=![]() 算法描述如表4.3所示。
算法描述如表4.3所示。
表4.3 改进的HSMM前向算法

同样可以定义后向变量为:βt(i,d)=P(![]() |(qt,τt)=(si,d))。观察系统状态转移过程可知,紧随状态(qt,τt)=(si,d)之后的下个状态必定为(qt+1,τt+1)=(si,d-1),当1<d或者(qt+1,τt+1)=(sj,d′),当1=d,j≠i,d′≥1。我们可以得出如下的后向递推公式:
|(qt,τt)=(si,d))。观察系统状态转移过程可知,紧随状态(qt,τt)=(si,d)之后的下个状态必定为(qt+1,τt+1)=(si,d-1),当1<d或者(qt+1,τt+1)=(sj,d′),当1=d,j≠i,d′≥1。我们可以得出如下的后向递推公式:
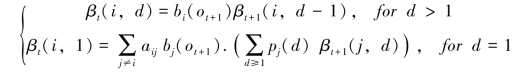 (https://www.daowen.com)
(https://www.daowen.com)
初始条件:βT(i,d)=1, d≥1。最后可得观察序列O的条件概率为:P(O|λ)=![]()
算法描述如表4.4所示。
表4.4 改进的HSMM后向算法

续表

