5.1.3 博弈论的经典案例——囚徒困境
在博弈论中有一个经典案例——囚徒困境(Prisoner's Dilemma),非常耐人回味。1950年,由就职于兰德公司的梅里尔·弗勒德(Merrill Flood)和梅尔文·德雷希尔(Melvin Dresher)拟定出相关困境的理论,后来由顾问艾伯特·塔克(Albert Tucker)以囚徒方式阐述,并命名为“囚徒困境”。
该案例是说有一天,一位富人在自己家中被害,财物被盗。警察在此案的侦破过程中,抓到两个小偷,并从他们的住处搜出了被害人家中丢失的财物。但是,他们矢口否认曾杀过人,辩称是先发现富翁被杀,然后只是顺手偷了点东西。为了弄清真相,警察将两人隔离,分别关在不同的房间进行审讯。警察说:“由于你们的偷盗罪已有确凿的证据,所以如果你们都坦白交代,可以判你们8年刑期。如果你单独坦白杀人的罪行,我判你无罪,立即释放,但你的同伙要被判9年刑。如果你拒不坦白,而被同伙检举,那么你就将被判9年刑,他判无罪,立即释放。”但是,如果两人都抗拒,那么,他们最多被判1年刑。
如果分别用-8、-9和-1表示罪犯被判刑8年、9年和1年的得益,用0表示罪犯被立即释放的得益,则我们可以用一个特殊的矩阵将这个博弈表示出来(见表5.2)。这种矩阵是表示博弈问题的一种常用方法,我们称这种矩阵为一个博弈的“收益矩阵”(Payoff Matrix)。
表5.2中“囚徒1”“囚徒2”代表本博弈中的两个博弈方,也就是两个囚犯,他们各自都有“不坦白”和“坦白”两种可选择的策略,因为这两个囚徒被隔离开,其中任何一人在选择策略时都不可能知道另一人的选择是什么,因此不管他们决策的时间是否真正相同,我们都可以把他们的决策看作同时作出的;矩阵中的每个元素都是由两个数字组成的数组,表示所处行、列代表的两博弈方所选策略的组合下双方的得益,其中第一个数字为选择行策略的囚徒1的得益,第二个数字为选择列策略的囚徒2的得益。对该博弈中的两个博弈方来讲,各自都有两种可选择的策略,因此该博弈共有四种可能的结果。在这些结果中,每个博弈方可能取得的最好得益是0,最坏得益是-9。两个博弈方的目标都是要实现自身的最大利益。那么他们该怎样选择策略?博弈的结果又会如何呢?
表5.2 囚徒困境博弈中的收益矩阵(https://www.daowen.com)
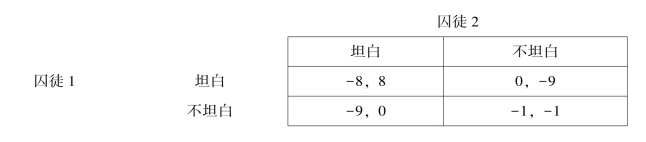
例如对囚徒1来说,囚徒2有“坦白”和“不坦白”两种可能的选择,假设囚徒2选择的是“不坦白”,则对囚徒1来说,“不坦白”得益为-1,“坦白”得益为0,他应该选择“坦白”,(因为根据参与者理性的原则,囚徒1只是根据自身利益最大的原则行事,不会关心此时另一方会被重判9年刑的问题);假设囚徒2选择的是“坦白”,则囚徒1“不坦白”得益为-9,“坦白”得益为-8,他还是应该选择“坦白”。因此在本博弈中,无论囚徒2有多少种策略,只考虑自身利益的囚徒2的选择是唯一的,那就是“坦白”,因为在另一方的两种可能选择的情况下,“坦白”给他自己带来的得益都是最大的。我们说“坦白”是囚徒l的一个占优的“上策”(Dominant Strategy)。
同样的,因为囚徒2与囚徒1的情况完全相同,因此囚徒2的决策思路和选择也与囚徒1完全相同,囚徒2在这个博弈中唯一合理的选择也是“坦白”,或者说“坦白”也是囚徒2的“上策”,所以该博弈的最终结果必然是两博弈方都选择“坦白”策略,都获得益-8,即都被判8年徒刑。
然而,仔细分析“得益矩阵”后我们可以发现,在这个博弈中,对这两个囚徒来讲,最佳的结果不是都“坦白”各得益-8,而是都“不坦白”,因为都“不坦白”各得益-1,显然比都“坦白”各得益-8好得多。
然而,由于这两个囚徒之间不能共谋,并且各人都追求自己的最大利益而不会顾及对方的利益,双方又都不敢相信或者说指望对方有合作精神,因此只能实现并不是最理想的结果。由于这种结果在博弈中又必然会发生,很难摆脱,因此这个博弈被称为“囚徒困境”。
