4.2.3 基于HSMM模型的系统状态预测算法
如果我们对网络系统在整个运行过程中的观测数据都获得以后,可以通过第3章所介绍的HMM模型计算出相应的网络安全风险值,进而可以描述出网络安全态势的历史。
状态预测的目标是在获取一段时间的观测信息,即部分观测信息后,对系统未来的状态进行预测。但HSMM的现有算法中要求已知所有观测记录才能进行系统状态测定,因此需要开发只有部分观测下的HSMM状态预测算法。
即假设已知t－1时刻之前一段时间的观测信号,预测系统t时刻处于某一状态的概率,即计算
其中:d是常数,表示记录的观测时间长度。将预测序列片断简记为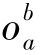
,即
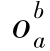＝(oa,oa＋1,…,ob),1≤a≤b≤T。
下面首先回顾上一节给出的HSMM的改进前向-后向(Forward-Backward,FB)算法,并以其为基础说明4.1式的计算方法。
由于HSMM不存在和HMM类似的尺度算法来防止溢出,在改进的Forward-Backward算法中,通过使用后验概率进行迭代从而防止溢出。
下面给出算法中定义的一些变量。
定义4.2 变量αt｜x(m,d),如4.2式所示,式中x取值可以为t－1或t,分别表示给定观测序列
预测或估计系统t时刻处于状态sm,状态持续时间为d的概率。
定义4.3 状态qt的边缘概率分布定义为变量γt｜x(m):
本节主要研究状态预测,所以仅讨论x＝t－1的情形。主要关注的是αt｜t－1(m,
定义4.4 定义变量
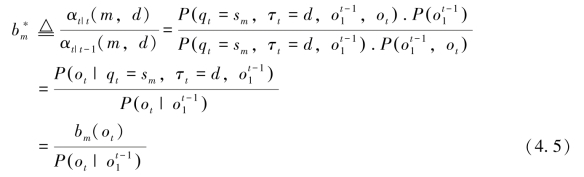
变量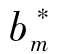
的计算过程如下:∵∀d,由其Markov性质,有:
定义4.5 给定观测序列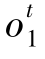
,某一个状态m结束于时间t的条件概率,记为εt(m),即εt(m)≜P(qt＝sm,τt＝1｜
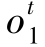)＝αt｜t－1(m,1)
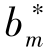(ot)。
定义4.6 给定观测序列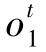
,某一个状态m开始于时间t＋1的条件概率,记为St(m),即St(m)≜P(τt＝1,qt＋1＝sm｜
)＝
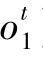因为状态(qt,τt)＝(sm,d)可能从其他状态转移过来,或者继续先前的状态即(qt－1,τt－1)＝(sm,d＋1),可以得到如下的前向递推公式:
其初始值为:αt＝1｜t＝0(m,d)＝πmpm(d)
将αt｜t－1对d求和得到qt的边缘分布:γt｜t－1(m)≜
该值即为在观测序列
已知的情况下,预测到的t时刻的系统所处状态qt的概率。
式4.5分母部分的计算: