最后的问题
在艾萨克·阿西莫夫1956年的短篇小说《最后的问题》(The Last Question)中,一个叫亚历山大·阿德尔的人在喝了酒之后,对宇宙的能源供应感到十分担忧。他的理由是,虽然能量本身是守恒的,但有用的那部分能量将不可避免被耗尽。物理学家将这种能带来变化的有用的能量称为自由能,这种能量是用来抗衡熵的量。随着熵的增加,自由能减少,变化也就不再发生。
在阿西莫夫的故事中,醉醺醺的阿德尔希望打败热力学第二定律,该定律宣称熵不会减少。他走向一台功能强大的自动计算机“穆尔蒂瓦克”(Multivac),问道:“如何才能使宇宙的总熵大幅度降低?”穆尔蒂瓦克顿了顿,答道:“数据不足,无法作答。”
你们可能不太知道阿德尔所担忧的热力学第二定律的具体内容,但是八成听说过这条定律的名字。这是我们在婴儿时期最先学到的事情之一:大部分东西都会损坏,而且有些东西坏了之后就无法再修复。会遭受这种悲惨命运的不只是妈妈最喜欢的杯子,你的车、你自己,甚至整个宇宙……一切事物最终都会损坏,而且无法修复。
生活经验告诉我们,事物的破损是不可逆转的,但是我们在上一章才刚刚说基本自然规律具有时间可逆性,二者之间似乎存在矛盾。在这种情况下,我们不能仅仅把这种不一致归咎于人类不可靠的感官,因为我们在许多比大脑要简单得多的系统中观察到了不可逆性。
例如,恒星在氢分子云中形成,它们会将氢聚合成更重的原子核,并以粒子的形式(主要是光子和中微子)释放出由此产生的能量。当一颗恒星耗尽所有原料时,它就会变暗,或者在某些情况下爆发,变成超新星。但我们从未见过相反的情况。我们从未见过一颗暗淡的恒星在吸收光子和中微子之后将重核裂变成氢,然后再扩散成氢云。自然界中像这样的过程比比皆是:煤的燃烧、铁的生锈、铀的衰变,我们从未见过相反的过程。
从表面上看,这一矛盾似乎无法调和。时间可逆定律怎么可能引发我们观察到的如此明显的时间不可逆现象呢?要理解这是怎么回事,需要先明确问题是什么。我刚才描述的所有过程在某种意义上都是时间可逆的,也就是说我们可以从数学上回溯演化规律并恢复其初始状态。也就是说,问题不在于我们不能将电影倒放,而是当我们倒放电影的时候,会立马发现有些事情不太对劲:满地的玻璃碎片跳起来将窗户填满,汽车轮胎将道路上的橡胶颗粒吸附得干干净净,雨伞上的水滴则向上升到空中。数学可能允许这样的过程,但这显然与我们观察到的现象不符。
理论的预期与我们直觉的预期之间存在偏差,是因为我们忘记了解释观测结果所需要的另一个要素。除了演化规律之外,我们还需要初始条件,但并非所有初始条件都是同等的。
假设你现在需要准备面糊,用来烤蛋糕。你把面粉放进碗里,加入适量的糖和盐,也许还有一些香精。然后你又加入了黄油,打入几个鸡蛋,还倒了一些牛奶。现在你开始搅拌,碗里的各种成分很快就会变成一种平滑的、毫无特征的物质。一旦发生这种情况,面糊就不再发生变化了。就算你继续搅拌,虽然分子依然会在碗里来回移动,但平均而言,面糊保持不变。最终一切都混合在一起,而宇宙的结局差不多也是这样:所有物质尽可能地混为一体,总的来说不再发生变化。
在物理学中,我们把总体上不变的状态称为平衡态,我们刚刚搅拌好的面糊就处于这样的状态。在平衡态下,熵达到最大值,换言之,自由能已经耗尽了。为什么面糊会达到平衡?因为这很容易发生。如果你使用搅拌器,它大概率会把鸡蛋和面粉搅在一起,但不大可能将两者分开。即使没有搅拌器,情况也不会有什么不同,因为配料中的分子不会完全静止,只是需要花费更久的时间。[1]搅拌器起到的只是快进键的作用。
其他的过程也是一样的:它们大概率只会朝一个方向发展。当破碎的窗玻璃掉落在地面上时,它们的动量一方面在地面上转化成微小的波纹,另一方面在空气中转化为冲击波,但地面和空气中的涟漪不大可能刚好以特定的方式自发地将玻璃碎片弹回正确的位置。当然,这在数学上是可能的,但是在现实中概率极低,我们从未见过这样的事情。
平衡态是你大概率最终达到的状态,同时大概率达到的状态又是熵最高的状态——这就是熵的定义。因此,热力学第二定律几乎只是同义反复而已。它仅仅说明,一个系统最有可能展现出可能性最大的结果,也就是熵增加。之所以说它几乎是冗余的,是因为我们可以计算出熵和其他可测量的量(比如压力或密度)之间的关系,从而量化并预测系统逐渐弛豫到平衡态的过程。
这些事情听起来好像稀松平常。罐子的破裂不可逆转,因为罐子自身无法愈合。嘁,这也算得上是重大发现?但你如果更加深入地思考这个问题,就会意识到一个重要问题。只有在不大可能回到先前的状态时,系统才会向可能性更大的状态演化。换句话说,初始状态一定要处于非平衡态。你能完成搅拌面糊这一工序的唯一原因就是鸡蛋、黄油和面粉还没有达到平衡。你能操作搅拌器的唯一原因就是你和你房间里的空气还没有达到平衡[2],并且我们的太阳和星际空间也没有达到平衡。所有这些系统的熵都远没有想象中那么高,换句话说,宇宙并不处于平衡态。
为什么呢?我们不知道,但我们给它起了个名字:初始条件假说(past-hypothesis)。该假说认为宇宙一开始处于一种低熵态,这是一种出现概率极低的状态。1从那之后宇宙的熵就一直在上升,并将继续升高,直到宇宙达到可能性最大的状态,并且总体上不再发生任何变化。
目前,在宇宙的某些地方,熵依然维持在较低的水平——比如你的冰箱里(实际上,我们的地球整体上的熵也不算高)——前提是这些低熵的区域会从其他地方获取自由能。目前地球获得的大部分自由能都来自太阳,有一些来自放射性物质的衰变,还有一些来自平凡而古老的引力。我们利用这些自由能带来了很多变化:学习、成长、探索、建设和维护。也许在未来的某个时刻,我们将成功地利用核聚变创造能源,这将大幅提升我们引发变化的能力。如此一来,假如我们能够英明地利用现有的自由能,就可以尽可能地把熵维持在较低的水平,让我们的文明存活数十亿年。但是自由能最终依然会被耗尽。
这就是为什么宇宙在时间上有一个前行的方向——时间之箭指向的正是熵增的方向,而非相反。熵的增加不是演化规律自身的性质带来的,因为演化规律是时间可逆的。只是演化规律把我们从一个不大可能的状态引向了一个可能性很大的状态,并且这一转变发生的可能性很大。如果要朝向另一方向发展,那就要让规律把可能性很大的状态变成不大可能的状态——这(几乎)不可能发生。
那么为什么我们不会变得更加年轻呢?涉及衰老的生物过程以及导致衰老的确切原因仍然是目前科学研究的一大主题,但是粗略地说,我们变老是因为身体内不断积累着很可能发生但不大可能自发逆转的错误。细胞修复机制不能无限制地、完美地纠正这些错误。因此,我们的身体一点一点地缓慢老化——我们器官的运作效率逐渐降低,皮肤的弹性逐渐下降,伤口的愈合速度也逐渐变慢。我们可能会患上慢性疾病、痴呆或癌症。最终,我们的身体会产生无法修复的损坏,某个重要脏器完全衰竭,某种病毒击溃了我们脆弱的免疫系统,或是某个血栓切断了大脑的氧气供应。你可以在死亡证明上找到许多不同的诊断,但它们只是细枝末节而已。真正杀死我们的是熵增。
到目前为止,我只是总结了目前接受度最高的有关时间之箭的解释,即它是熵增和初始条件假说共同导致的结果。现在我们要继续深入地考察,其中哪些是我们确切地知道的,哪些则属于猜测。
将宇宙的初始条件设为低熵态的初始条件假说,是我们目前用于描述观测结果时所必需的理论。就目前而言,该假说差强人意,而我们也尚未找出比它更好的解释,现有理论无法回答为什么宇宙的初始状态会是这样的。宇宙一定曾经处于某种初始状态,但我们无法解释初始状态本身,只能检验某个特定的初始状态是否具有解释力,以及它能否推导出与观测结果一致的预测。初始条件假说的好处在于,它能够解释我们所看到的东西。然而,要想用除更早的初始状态以外的任何东西来解释当前的初始状态,我们就需要另一种类型的理论。
当然,物理学家提出过不同的理论。例如,在罗杰·彭罗斯的共形循环宇宙学理论2中,宇宙的熵实际上在每一阶段结束时都遭到了破坏,因此下一个阶段的宇宙会从低熵态重新来过。这的确解释了初始条件假说,但也付出了代价,那就是将信息永久地销毁了。肖恩·卡罗尔认为新的低熵宇宙是从一个更大的多元宇宙中创造出来的,而这一过程可以无穷无尽地持续下去。3朱利安·巴伯(Julian Barbour)则假设宇宙起源于“雅努斯点”(Janus point)[3],时间的方向在此发生了改变,因此实际上有两个宇宙起源于同一时间点。他认为,熵不是一个值得探讨的物理量,我们应该将目光转投向复杂性(complexity)。4
我接下来要说什么你可能已经猜到了:这些想法都很好,唯独缺少证据支撑。你尽可以相信它们,毕竟我也不认为有什么证据能证明它们是错的,但是不要忘记,它们只是猜测罢了。
不过我确实非常赞同朱利安·巴伯的观点。这并不是因为巴伯认为时间会改变方向(我对此没有什么特别的看法),而是因为我也不认为熵在描述整个宇宙时有多大作用。要想知道我之所以会这么想的原因,那就得先搞懂我在“总的来说”“平均而言”这种模棱两可的表述之下所掩盖的数学。
从理论上讲,熵是关于某个系统在保持某些宏观特性不变的情况下可能具有的所有不同构型数量的表述。例如,你可以思考为了得到一团平滑的面糊,有多少种将分子(糖、面粉、鸡蛋等的分子)放入碗中的方法。分子的每一种特定的排列都被称为系统的一种微观状态,而微观状态就是某种构型的全部信息,比如每个分子的位置和速度等等。
另一方面,平滑的面糊即为所谓的宏观状态,也就是我之前所说的不会改变的平均状态。宏观状态可以由许多在某些意义上相似的不同微观状态构成,比如面糊中的所有微观状态就都是相似的,因为所有成分都近似于平均分布。我们之所以会选定这样的宏观状态,是因为我们无法将面糊中一种近乎完全均匀的分布与另一种区分开来。对我们来说,它们看起来都差不多。
鸡蛋、黄油、糖和面粉尚未搅拌开的初始状态也是一种宏观状态,但它与面糊有很大的不同——你可以轻而易举地分辨出搅拌前和搅拌后的状态。若想获得搅拌前的状态,你就必须将分子按照正确的分区放好:鸡蛋分子放在鸡蛋区域,黄油分子放在黄油区域,等等。初始状态下的分子是有序的,而搅拌之后就不再有序了,因此也经常有人将熵增描述为秩序的破坏。
熵的数学定义是一个与宏观状态相关联的数字:构成该宏观状态的微观状态数。如果你能通过许多微观状态得到一个宏观状态,该宏观状态的熵就很高;反之,如果你只能从相对较少的微观状态得出一个宏观状态,该宏观状态的熵就很低。在搅拌后的面糊中,分子是随机分布的,它比最初未经搅拌的面糊具有更多微观状态。因此搅拌后的面糊具有较高的熵,而搅拌前的面糊则具有较低的熵。(https://www.daowen.com)
为了更加直观地理解熵的概念,我们假设现在只有两种原料,分子数也从1025这个量级降低到36个,其中一半是面粉,一半是糖。我把它们画在方格里面,其中灰色方块标记的是面粉分子,白色方块标记的则是糖分子(参见图4)。最初这两种物质之间泾渭分明:面粉在下面,糖在上面(参见图4a)。现在我们可以通过随机交换两个相邻(纵向或者横向均可)方块的位置来模拟搅拌器的作用,我画出了第一步作为示范(参见图4b)。
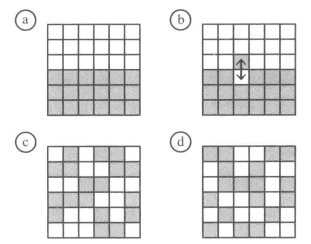
图4 简化的搅拌模型。灰色的方块代表面粉,白色的方块代表糖。搅拌会随机交换相邻两个方块的位置
如果我们继续这样随机交换下去,分子最终会呈现出随机分布的样子(参见图4c)。分子不会一直待在同一个地方,而是均匀地混合在一起。进一步搅拌后,它们可能会变成图4d的模样。换句话说,大量的随机交换会得到与你把分子随机扔进碗里差不多的平均分布。所以我们不需要考虑搅拌器具体是怎么交换的,只关注初始分布和最终分布的区别即可。
现在我们可以对所谓平滑面糊的宏观状态下一个定义,即代表糖和面粉的方块大致均匀地分布在画面的上下两半,比如有8~10个糖分子分布在上半部分(参见图4c和图4d)。重点在于,这一宏观状态下的微观状态数要比最初完全分离的微观状态数多得多。事实上,如果你不区分同一类型的分子,那么初始的微观状态就只有我在左上角画出的这一种,但是最终大致呈现出均匀分布的微观状态则会有很多种。
这就是熵在近似均匀分布的状态下最大的原因,也是这两种物质不太可能重回未搅拌状态的原因——这需要一条非常具体的随机交换顺序。你搅拌的分子越多,恢复原样的可能性就越低。恢复原状的可能性很快就会变得极为渺茫,哪怕你持续搅拌十亿年也几乎不可能看到这种事情发生。
既然你已经知道了如何正式定义熵,那我们就仔细研究一下这个定义:熵度量了可以构成某一宏观状态的微观状态的数量。请注意“可以”这个词。系统在某一特定时刻下只会对应一种微观状态,它“可以”处于任何其他状态的说法是反事实的——这里指代的是现实中并不存在,而只在数学上存在的状态。我们将这些状态纳入考虑,仅仅是因为我们并不知道系统的真实状态是什么样。
因此,熵度量的实际上是我们的无知程度,而不是系统的实际状态,它量化了我们认为不重要的微观状态之间的差异。我们对于面糊中具体的分子排列方式并不怎么关心,所以我们将其统称为一种宏观状态,并宣称其为“高熵态”。
如果你想计算一个系统演化到特定宏观状态的速度,那么这样的推理就很有意义。因此,熵的概念在它被发明的领域中起到了中流砥柱的作用,如蒸汽机、冷却循环、电池、大气环流、化学反应等。日常经验告诉我们,这种推论可以很好地描述我们对上述系统的观察结果。
然而,如果我们想要了解整个宇宙的情况,那么这样的推理就显得不够充分了,原因有三。首先,在我看来最重要的原因在于,我们脑海中宏观状态的概念已经暗含了我们所理解的变化过程,因此熵的概念是不充分的。根据我们对宏观状态的定义,即便熵已经达到最高值,状态也依旧会发生变化(即使面糊看起来已经相当平滑,你仍然不断地在碗中搅拌它)。我们认为这些变化无关紧要,但这只是基于我们现有的理论所做出的判断。我们并不知道,一旦未来发展出新的理论,这种情况还会不会继续保持下去。
我在图5中说明了上述观点。你可以把它们想象成宇宙末日的两种可能的微观状态,10个孤立的粒子随机分布在空旷的空间里。如果第一个微观状态(左)变成第二个微观状态(右),你不会认为这是一种很大的变化。你会把它们平均化,然后统称为同一种宏观状态。
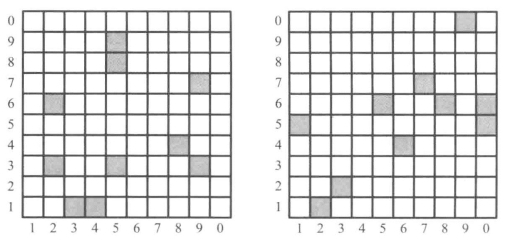
图5 表面上看起来是非常相似的随机排列,但实际上高度有序,且彼此间差异巨大
但是请仔细观察这些粒子在网格上的位置。在左边这张图中,粒子位于(3,1)、(4,1)、(5,9)、(2,6)、(5,3)、(5,8)、(9,7)、(9,3)、(2,3)以及(8,4)这10个坐标;在右边这张图中,粒子则位于(0,5)、(7,7)、(2,1)、(5,6)、(6,4)、(9,0)、(1,5)、(3,2)、(8,6)以及(0,6)这10个坐标。对数字足够敏感的人只要看一眼就能认得出,这些坐标分别是圆周率π和欧拉-马歇罗尼常数γ的前20位。5这些粒子的分布可能看起来没什么特别的地方,但是有能力掌握排列顺序的人可以明确地分辨出来,它们是由两种完全不同的算法创造出来的。
诚然,这样的结构只是特例,它并不适用于我们实际接触的理论,但它说明了一个总体的观点。在把“相似”的状态放在一个宏观状态下之前,我们首先要给“相似”下定义。我们需要从当前的理论中归纳出这一概念,而这些理论又是基于我们眼中的“相似”而建立的。但是改变相似的定义就意味着改变熵的定义。借用戴维·博姆(David Bohm)创造的术语来说,为当前理论所量化的显序(explicate order),可能有一天会揭示出我们迄今未曾触碰的隐序(implicate order)。6
在我看来,这就是热力学第二定律不能被我们用于宣判宇宙命运的最终结论的主要原因。我们对熵的定义基于我们目前对宇宙的认知,而我认为这从根本上来说并不一定准确。
对宇宙的熵的讨论持怀疑态度还有两个别的原因。第一,如果一个理论允许存在无限多的微观状态,那么计算和比较它们的数量就会变得相当棘手,而这是所有连续场论都会面临的窘境。虽然在这样的情况下我们仍然可以定义熵,但这个量是否还有意义就有待商榷了。在无穷大和无穷大之间进行比较通常不是个好主意,因为其结果取决于你如何定义“比较”,所以得出的所有结论在物理上都只是无根之木。
最后一个理由是,我们实际上并不知道应当如何定义引力或者时空的熵,但它们在宇宙的演化过程中扮演了最为关键的角色。你可能已经注意到,根据我们目前的理论,宇宙中的物质最开始是近乎均匀分布的等离子体。根据初始条件假说,等离子体一定处于低熵态;但是我之前也提到过,平滑面糊的熵很高。两者之间的矛盾要怎么调和呢?
如果考虑引力使得早期宇宙中极不可能出现几乎均匀的高密度等离子体,那么矛盾自然就消解了。引力会将物体聚集起来,但出于某种原因,物质在宇宙形成初期较为分散,这就是初始状态的熵很低的原因。一旦它随着时间逐渐演化,等离子体就会开始聚集,并形成恒星和星系——因为这些事件发生的可能性很大。这种情况在面糊中不会发生,因为引力在数量如此稀少且密度相对较低的物质当中还不够强。正是引力的作用不同,才使得面糊和早期宇宙处于截然不同的情况,这就是为什么前者具有高熵,而后者处于低熵状态。
然而,为了定量分析这个例子,我们必须理解要如何把熵分配给引力。虽然物理学家已经做了一些尝试,但我们仍然不知道怎样才能做到这一点,因为我们不知道如何将引力量子化。
出于这些理由,我个人认为热力学第二定律很不可靠。如果我们进一步理解引力和量子力学的原理,当下由该定律得出的结论可能会不再有效。
在阿西莫夫的短篇小说中,宇宙逐渐变冷变暗,所有恒星最终都燃烧殆尽。我们所知的生命已不复存在,取而代之的是宇宙意识,即跨越星系、在空间中自由游弋的无实体意识。人们找到穆尔蒂瓦克系列的最后一个且最为强大的版本“宇宙智能电脑”(Cosmic AC),再次问出了如何使熵减少的问题。然而,它再一次冷漠地回答道:“数据不足,无法得出有意义的回答。”
在故事的结局中,人类的最后一缕意识也与AC融合在一起,物质与能量都消失了,只有AC存在于“超空间”里。最终,AC完成了所有的计算。
AC的意识包含了曾经宇宙中的一切,在如今的混沌之中沉思,一步一步地贯彻着计划好的程序。然后AC说道:“要有光!”于是就有了光。7
