预测不可预测性
本书的大部分篇幅都在讨论我们从物理学中学到的有关我们自身存在的东西。我希望你在这段旅程中感到愉快,但也许有时候你不可避免地会有这样的感受:这些内容非常有趣,但是对解决现实中的问题没什么帮助。因此,在本书接近尾声之际,我想花几页篇幅来谈谈理解不可预测性有可能在未来产生哪些实际后果。
我们回到天气预报的问题上来。我们不打算在这里解决第4个千禧年问题,所以为了论证的方便起见,我们不妨假设纳维-斯托克斯方程的解在有限时间之外确实有的时候是不可预测的。我之前已经解释过了,纳维-斯托克斯方程并不是基础的,而是从描述所有粒子的量子理论中涌现出来的。但是不管它基础与否,我们在充分理解其性质之后都可以合理地期望,通过求解这一方程可以达到什么目的。
例如,由于一条数学定理告诉我们天气预报无法得到改进,于是我们可能会得出这样的结论:投入大量资金来建设更多的气象测量站没有意义。但无论纳维-斯托克斯方程是否在根本上是正确的,这一投资建议的合理性都不会受到任何影响;其重要性只会在气象学家在实践中使用它的时候才能体现出来。
当然,这个例子过于简化了。实际上,预测的可行性取决于初始状态:有些天气状况的变化趋势很容易进行长期预测,有些则不然。我要再一次强调,理解什么是可预测的可不仅仅是无聊的数学推导。我们有必要知道什么是可以改进的,以及可以通过什么方式来改进。
让我们进一步探讨一下这个想法。假设我们非常擅长预报天气,甚至可以准确地计算出纳维-斯托克斯方程何时会出现不可预测的情况。这样一来,我们就能找出,如何适时小幅扰动气象系统,将天气切换成我们喜欢的样子。
科学家确实考虑过像这样干预天气,例如,防止热带气旋发展成飓风。他们对飓风的形成有足够的了解,从而想到了如何阻止其发展的想法。目前面临的主要问题是,天气预报还不足以准确地指出应该在何时何地实施干预。但是像预防飓风这种控制天气的想法并不是天方夜谭。如果计算能力可以继续提高,那么我们有可能在几十年内就能真正做到这一点。
混沌控制在其他系统中同样发挥着作用——例如核聚变装置中的等离子体。这种等离子体是由原子核以及脱离了它们的电子组成的粒子汤,温度超过1亿摄氏度。等离子体中有时会发展出不稳定性,从而对外面的安全壳造成严重破坏。因此,如果不稳定即将出现,那么聚变过程必须立刻中断。这是聚变反应堆难以高效运转的主要原因之一。
不过,如果我们能够预测到不可预测的情况何时会出现,那么等离子体不稳定性在理论上就是可以避免的;如果我们能够控制等离子体,那么就连导致其不稳定的情况都可以避免。换句话说,如果我们知道方程的解从什么时候开始变得不可预测,我们就可以利用这一点将这种状况扼杀在萌芽之中。
这不仅仅是纸上谈兵,最近有一项研究正是对此展开了调查。18有个科研团队训练了一套人工智能系统,用以识别预示着等离子体不稳定性即将到来的数据模式。他们只用了公开发表的数据就成功做到了这一点。在超过80%的情况下,他们可以提前1秒钟正确识别出即将出现的不稳定性;如果把预警时间放宽到30毫秒,那么成功率几乎是100%。
诚然,他们没能完成主动的风险控制,所谓的分析只是事后诸葛亮。然而,考虑到分析结果的准确性,也许未来主动控制将成为可能。最终,一座高效节能的聚变电站可能会是一个只需运用高级机器学习进行微调即可解决的问题。
类似的思路同样适用于表面上完全不同,但是与等离子体爆炸和天气预报有许多相似之处的系统,例如股票市场。今天,一大批金融分析师试图通过预测股票和金融工具的买卖来赚钱,这项任务甚至还包括预测其竞争对手的预测。但每隔一段时间,他们就会被打个措手不及。股市崩盘,卖家恐慌,每个人都在相互指责,而世界经济则陷入衰退。(https://www.daowen.com)
但是想象一下,如果可以预知麻烦什么时候会找上门来,我们也许就能及早全身而退。
为了避免祸事缠身,我们不仅要掌握其不可预测性,还要认识到它的不可计算性。以经济系统为例,这是一种自组织、自适应的系统,其目标是优化资源分配。一些经济学家认为,这种优化在一定程度上是不可计算的。这显然不是好事,因为这意味着经济系统无法发挥作用。或者更确切地说,我们作为经济系统中的主体无法完成任务,因为交易没有取得预期的成果。
为了创造一个能够(在有限时间内)实现想要的优化的经济系统,我们发展出了可计算经济学这一研究方向。19与不可预测性一样,将可计算经济学与不可能定理扯上关系的并不是证明某个问题(在这里指的是“如何实现资源的最优分配”)的解决方案从根本上是不可计算的(它有可能是也有可能不是),而是它对于我们目前掌握的手段来说是不可计算的。
然而在其他情况下,也许有时我们想要做的是触发而非避免不可预测性,因为随机性有时也会带来收益,比如可以防止计算机在搜索最优解的时候遇到困难。
你可以把计算机算法想象成一种当你把它扔到山里的时候总会向上爬的装置,地形代表某个问题可能的解法,高度则代表一些你想优化的量,比如预测的准确性。最后,计算机算法会坐在一座小山的山顶上(局部最优),但实际上你想找到的是最高的那座山(全局最优)(参见图19)。添加随机噪声可以防止这种情况发生,因为这样算法就有机会能碰巧发现一个更优的解。因此,随机要素可以提高数学代码的效能,这可能与我们的直觉相违背。
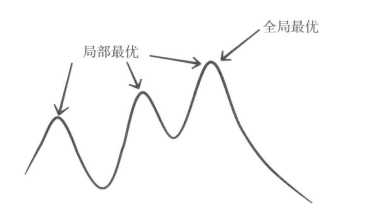
图19 局部最优与全局最优
在计算机算法中,随机性可以通过生成(伪)随机数来实现,无须动用复杂的数学定理。但是在其他情况下,不可预测性也可能有助于优化的过程,比如小幅度的随机性有助于提高经济系统的效率。更有趣的是,不可预测性有可能是创造性的一个基本要素,因此人工智能在未来也可以利用这种特性。20
目前,人工智能已经比我们更善于从大量数据中寻找规律,这将给科学研究带来极大的改变。人类科学家寻找的是在环境变化下能够维持鲁棒性且易于推断的普遍规律,迄今为止的大多数科学研究都是这样进行的。现在,我们可以使用人工智能来寻找那些更难识别的规律,个体化医疗正是在这样的趋势下诞生的,我们很快就能看到更多像这样凭借人工智能而蓬勃发展的新兴领域。科学家将不再苦苦追寻普遍规律,而是将越来越多的精力放在研究对象所依赖的外部参数上——生态学、生物学,以及社会科学和心理学领域的科学研究已经迈向了这条道路,这里大有可为,潜力无限。
物理学家也应该注意到这一点,他们发现的普遍规律相对于目前尚未认识到的复杂性来说可能只是冰山一角。虽然我的同事们认为他们正在接近最后的答案,但我认为我们才刚刚触及问题的表面。
