真空中的大脑
我们终将归来
在时间的尽头
就像缸中的大脑,四处游荡
只有纯粹的思想。
——扎比内·霍森菲尔德《薛定谔的猫》12
我们已经认识到现实不过是大脑根据感官的输入而产生的复杂结构,因此,只要输入发生改变,我们对现实的感知也就会改变。这样的认识已经随着《黑客帝国》(主人公在电脑模拟的环境中成长,却发现现实世界和他所想象的样子相去甚远)、《盗梦空间》(主人公艰难地设计出区分梦境与现实的方法)以及《移魂都市》(主人公的记忆每到午夜就会被重置)等电影的风靡而逐渐渗入流行文化,尽管这些描述往往不会表明现实归根结底是不存在的。有些禁区连好莱坞都不会轻易触及。
你可能只是缸中或者空无一物的宇宙里的一个孤零零的大脑,感官的输入为你创造了作为人类在地球上生存的幻觉。这并不是什么新奇的想法,而是一种被称为唯我论的古老哲学。这种理念认为,我们无法真正确定除我们自身之外的任何东西存在。我们通常认为,这种思想最早的书面记录来自2500年前的希腊哲学家高尔吉亚(Gorgias),但是更加经常与唯我论联系在一起的人是勒内·笛卡儿,他将其总结为“我思故我在”,并且还补充说明,除了“我”以外的一切都可以被怀疑。
你可能会寄希望于物理学来解决这个难题,但是它做不到,于是情况变得更加糟糕了。之所以物理学解决不了这个问题是因为,我在阐述熵增时忽略了一个有些麻烦的细节:熵实际上并不是总会增加。而熵一旦减少,就会发生奇怪的事情。
我们再回到之前那个包含36个方格的简化版面糊搅拌模型。假设你已经达到了高熵态,画面的上半部分有8~10个灰色方块,此时的面糊处于平滑的宏观状态。问题在于,如果你继续随机交换相邻的方块,状态不会永远保持平滑。每隔一段时间都有可能偶尔会出现上半部分只有7个糖分子的情况,继续下去的话甚至还有可能出现只有6个糖分子的情况。这种情况不太可能会持续很长时间,面糊可能很快就能重回平滑状态。但是如果你持续不断地进行搅拌,那么总会出现上半部分只有5、4、3、2、1个,甚至只有0个灰色方块的情况。这也就意味着你又回到了初始状态,熵似乎减少了。
上述推导过程正确无误,熵的特性就是这样。当你使系统的熵达到最大值,达到平衡态之后,熵有时也会降低。系统有可能会出现细微的非平衡态涨落,且规模越大的涨落出现的可能性越低。在真正的搅拌面糊的过程中,熵大幅减少的可能性极低,哪怕你从大爆炸时就开始搅拌,也不会看到这种事情发生。但如果你搅拌的时间足够长,鸡蛋最终会重新组合到一起,黄油也会单独聚成一团。这并不是纯粹的数学猜想——熵的自发减少可以观测,而且我们已经在一些小型系统中观测到了这样的现象。例如,有人观测到偶尔会有水分子从随机运动中获得能量,形成漂浮在水中的小水珠,这种瞬时的行为违背了热力学第二定律。13
熵的涨落会引发下面这一问题。我们如果把有关宇宙的所有知识都综合起来,就会发现宇宙似乎会无限制地膨胀下去。随着熵的不断增加,宇宙变得越来越无趣。最终,当所有的恒星悉数消亡,所有的物质都坍缩成黑洞,所有黑洞都蒸发殆尽,宇宙中只剩下稀疏的辐射和偶尔相撞的粒子。
但这并不是故事的结局,因为无限代表着极其长久的时间。在无限长的时间里,任何可能发生的事情最终都会发生,哪怕只有一丝一毫的可能。
这意味着在那个无聊、高熵的宇宙中,会有一些熵自发减少的区域。其中大部分都是小规模事件,但总有一天会出现较大的涨落,在极其偶然的情况下可能会形成糖分子之类的粒子。耐心等待一段时间,你就能看到一个完整的细胞。如果继续等待下去,也许最终会有一个功能完整的大脑从高熵的粒子汤里面横空出世,并且拥有足够的时间去思考“我在这里”,然后又在熵增的洪流下消失得无影无踪。为什么它又消失了?因为这是最有可能发生的事情。
这些自我意识的低熵涨落就是玻尔兹曼大脑,以路德维希·玻尔兹曼的名字命名,他在19世纪末提出了我们如今在物理学中所使用的熵的概念。彼时量子力学尚未诞生,玻尔兹曼所关注的是粒子集团中的纯统计涨落,但是后来发现的量子涨落放大了这个问题。在量子涨落的作用下,低熵的物体(比如大脑)甚至可以在真空中凭空出现,随即又消失不见。
你可能会觉得说这种涨落能产生大脑有些言过其实了,这么想的不止你一个人。物理学家塞思·劳埃德(Seth Lloyd)在谈到玻尔兹曼大脑时说:“这种东西连巨蟒剧团的考验都经受不住[5],赶紧停手吧!这太荒唐了!”14李·斯莫林也曾经对我说过:“为什么是大脑?为什么从来没有人谈论过诞生于涨落的肝脏?”他们的观点不无道理,但我支持肖恩·卡罗尔的观点15:玻尔兹曼大脑的概念中有一些值得我们学习的宇宙学知识。
玻尔兹曼大脑的问题和大脑本身并无太大关联,而在于如此大规模的涨落有可能会发生的这一事实导致了预测与观测结果相脱节。别忘了,熵越低,发生涨落的可能性就越小,因此熵又必须足够小,才能解释你目前为止所观察到的一切,最起码也是输入了你在生活中的那些信息的你的大脑。但是这个理论以压倒性的概率预测了,你接下来会看到地球消失,而系统则弛豫到平衡态。显然,这样的事情尚未发生。再等等……好吧,还是无事发生。于是,你将这一预测彻底推翻了。
如果一个理论推导出的预测与观测结果不一致,那就说明这个理论一定存在一些问题,可是问题出在哪里呢?我之前提到的我们对于熵的认知漏洞(引力、连续场)有一定的嫌疑,但罪魁祸首更有可能是玻尔兹曼大脑理论中的另外一条假设:并非所有类型的演化规律都能导致所有可能发生的涨落。(https://www.daowen.com)
每种涨落最终都会发生的理论被称为遍历理论。我们之前提到的面糊混合模型是遍历的,玻尔兹曼以及他那个年代的其他科学家所研究的模型也都是遍历的。遗憾的是,我们目前在基础物理学上所使用的理论是否具有遍历性,目前还是一个未解之谜。
150年前,有一些物理学家很关心粒子之间相互碰撞后改变运动方向的问题,他们发出了这样的疑问:“一个房间里所有的氧原子到底需要多长时间才能聚集到房间的一个角落中去?”这是个好问题(答案是非常非常久,所以你不用担心了),要想讨论如大脑这般复杂的东西究竟是如何被创造出来的,你需要先让粒子粘连到一起。用物理学家的话来说,它们必须形成束缚态。例如,质子就是由三个夸克组成的束缚态,强核力将它们维系在一起;恒星也处于束缚态,它们所受到的是引力的束缚。只靠粒子之间的相互碰撞可远远无法创造出我们今天所看到的宇宙。目前我们还不清楚引力和强核力是否具有遍历性,因此玻尔兹曼大脑理论与之并不矛盾。
事实上,我们可以将该论述逆转过来,从而得出如下结论:我们的基础理论中至少有一个不能具有遍历性。这就是我认为玻尔兹曼大脑很有意思的原因——我们可以从中获知一些自然规律所必备的性质。但是你不必担心自己是一个位于真空中的孤单大脑,因为如果是这样的话,你肯定已经消失了。如果还没有消失,那就再等等,或许就是现在……
玻尔兹曼大脑是一种通过矛盾来引导争论的论证方式(如果自然规律是遍历的,那么你就会观测到极不可能发生的事件),但你基本上不太可能是这样一个大脑。不过,我认为玻尔兹曼大脑在科学文献中留下的书面记录里面潜藏着更深层次的信息。
基础物理学让我们得以更加仔细地观察现实,但我们观察得越仔细,现实就会变得越发不可靠。我们对数学的大量使用是主要原因之一。随着对自然的基本描述越来越脱离我们的日常经验,我们不得不依赖数学的严谨性,而这种程度的依赖会造成诸多影响。用数学来描述现实意味着,同样的观测结果可以用许多不同且等价的方式进行解释,而这仅仅是因为有很多组不同的数学公理可以对所有有效数据给出完全相同的预测。因此,假如你想将“现实”分配到某种解释头上,你都不知道应该选择哪一个。
例如,在艾萨克·牛顿的时代,认为引力真实存在是毫无争议的。这是一种非常有效的数学工具,从炮弹的轨迹到月球的运行轨道,好像没有什么它计算不了的东西。但是后来阿尔伯特·爱因斯坦横空出世,他告诉我们,被我们称为引力的效应是由时空弯曲所引起的,引力并不是“力”。这是否意味着引力在爱因斯坦那个时代就不存在了呢?不,这只是意味着,什么东西是真实的取决于人的观念,而大多数科学家都不会轻易下定论。
你可能会说,引力并不是从爱因斯坦的时代才开始不存在的,而是从一开始就没存在过,爱因斯坦之前的科学家全部大错特错!但是在这种情况下,你就不能声称我们现有的理论中的任何东西是真实存在的,因为这些理论没准儿哪一天就会被更好的理论取而代之。空间?电子?黑洞?电磁辐射?你也不能说这些东西是真实的。这种现实的概念也会让大多数科学家想要回避。
哪怕不考虑将来可能发生的范式转移,你要使用什么样的数学来描述观测结果也是模棱两可的,因为在物理学中存在着对偶理论。两个对偶的理论可以用完全不同的数学形式描述同一个可观测现象,就像这幅图一样(参见图6),它要么是兔子,要么是鸭子,但它到底是一只兔子还是一只鸭子呢?16实际上,这只是一个由黑色线条构成的形状,只不过你可以用两种方式来解释它。
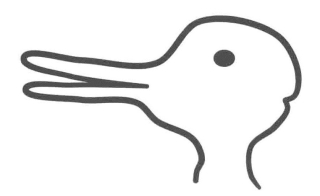
图6 这是一只兔子还是一只鸭子?
在物理学中,最著名的对偶理论莫过于规范/引力对偶。这是一种数学等价关系,它在更高维的引力理论(其中包含时空弯曲)和无引力条件下比前者低一维的粒子理论(例如在平直时空当中)之间建立了联系。在这两种理论当中,你都拥有计算可测量物理量(比如金属的导电性)的方法。这些引力或者粒子理论的数学元素是不同的,它们各自的计算方法也不同,但是预测结果完全相同。
现在,对于规范/引力对偶能否准确描述我们在宇宙中所观察到的东西仍然存在争议。很多弦论研究者都认为结果是肯定的,而我也认为它很有可能正确地描述了某些类型的等离子体,而这些等离子体与某些特定类型的黑洞是对偶的(或者也可以说是一些黑洞与某些种类的等离子体对偶)。但是对于我们的讨论来说,这种特殊的对偶理论能否准确描述自然其实无关紧要。仅仅是对偶理论有可能存在,就支持了从未来范式转移的威胁所得出的结论:我们不能将“现实”分配到一个理论的任何表述形式之上。(量子力学的几种不同的诠释是另外一个例子,但是请允许我将该内容放到第5章中讨论。)
正是因为如此令人头疼的问题,哲学家在实在论的基础上发展出了结构实在论。结构实在论认为,在一个理论中,真实的部分是其数学结构(也就是图6中既像兔子又像鸭子的形状),而不是其中任何一个表述形式。爱因斯坦的广义相对论在结构上包含了之前被称为引力的东西,因为我们可以在一种名为“牛顿极限”的近似条件下推导出这种力。这个极限不能在所有情况下都准确地描述我们的观测结果(它在接近光速以及时空高度弯曲的情况下就会失效),但仅凭这个并不意味着它不真实。
在结构实在论中,你可以认为引力是真实的,即便它只是一种近似;你也可以认为时空是真实的,即便它可能有一天会被更基本的东西(也许会是一个巨大的网状结构)所取代。因为无论更好的理论是什么样,它都必须能在适当范围内重现我们目前所使用的结构。这样一切就说得通了。
如果我是一名实在论者,那我一定会支持结构实在论。但我并不是,原因在于我无法排除这样的可能性:我是一个缸中之脑,我脑海中所有关于自然规律的知识都是精心设计的幻觉。根据我在生活中所学到的一切,或许我可以说服自己得出这样的结论:我不可能是一个毫无特征的宇宙中的一个涨落。但这仍然不能证明除了我的大脑之外存在其他宇宙。唯我论虽然可以被看作一种哲学,但它也萌生自生物学上的事实。我们在自己的大脑中是孤立的,并且至少到目前为止,我们还不可能直接推断出除了我们自己的思考之外还有什么其他东西存在。
不过,即便我认为自己永远不能完全确定除了我自己之外的任何东西存在,我也发现耽溺于这样的哲学当中完全是浪费时间。也许你并不存在,而我写这本书也只是我的幻觉。但如果我无法分辨幻觉和现实,那为什么还要费力去尝试呢?现实当然是一个足够方便也足够好的解释。因此,出于实际应用的目的,我会把我的观察当作真实的来处理,同时承认自己不能完全确定这本书或是它的读者是否真的存在(如果有人问起的话)。
