2.1.3 密码体制
密码学是一门古老的学科,它通过把人们能够读懂的消息变换成不易读懂的消息来隐藏消息内容,使窃听者无法理解消息的内容,同时能让合法用户把变换的结果还原成能够读懂的消息。
一个密码系统,通常简称为密码体制(Cryptosystem),由五部分组成。
(1)明文空间M,它是全体明文的集合。
(2)密文空间C,它是全体密文的集合。
(3)密钥空间K,它是全体密钥的集合。其中,每一个密钥K均由加密密钥ke和解密密钥kd组成,即K=<ke,kd>。
(4)加密算法E,它是一族由M到C的加密变换。
(5)解密算法D,它是一族由C到M的解密变换。
对于每一个确定的密钥,加密算法将确定一个具体的加密变换,解密算法将确定一个具体的解密变换,而且解密变换就是加密变换的逆变换。对于明文空间M中的每一个明文m,加密算法E在密钥ke的控制下将明文m加密成密文c,而解密算法D在密钥kd的控制下将密文c解密出同一明文m。如果一个密码体制的ke=kd,或者由其中一个很容易推出另一个,则称为对称加密体制、单密钥加密体制或者传统加密体制,否则称为双密钥加密体制。如果在计算上kd不能由ke推出,这样将ke公开也不会损害kd的安全,于是便可将ke公开。这种密码体制称为公开密钥加密体制,简称为公钥加密体制。
在对称加密体制中,加密算法E和解密算法D取决于相同的密钥k(如图2-2所示)。对于明文m,发送方Alice利用加密算法E和密钥k将明文m加密成密文c,有c:=E(k,m)。对于密文c,接收方Bob利用解密算法D和密钥k将密文c解密成明文m,有m:=D(k,c)。因此,在对称加密体制中,对于明文m,有
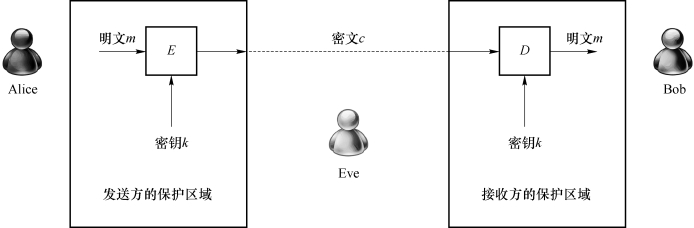
图2-2 对称加密体制示例
D(k,E(k,m))=m
为了使用对称加密体制,合法的通信双方首先必须商定一个会话密钥,然后双方就可以利用这个会话密钥进行秘密通信。
在公钥加密体制中,加密算法E和解密算法D取决于不同的密钥k=(ke,kd)(如图2-3所示)。ke是公开的加密密钥,简称公钥;kd是保密的解密密钥,简称私钥。发送方Alice利用Bob的公钥ke加密明文m得到密文c:=E(ke,m),并把密文c传送给Bob。接收方Bob利用自己的私钥kd解密密文c得到明文m:=D(kd,c),即
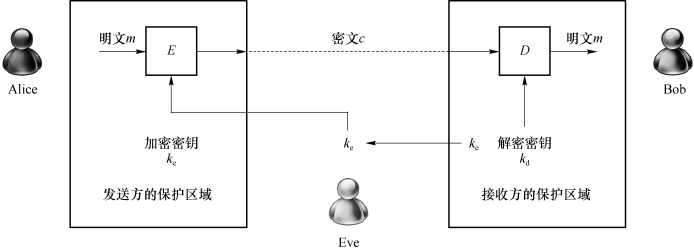
图2-3 公钥加密体制示例
D(kd,E(ke,m))=m
利用公钥ke加密明文m是容易的,但不知道私钥kd,从密文c推断明文m是困难的。保密性要求从密文中不能得到有关明文的任何信息。不严格地说,如果从密文中提取有关明文的任何信息是不可行的,就称这个加密体制是安全的。公钥加密方法要求更复杂的计算,比传统对称加密方法的效率低,因此,对称加密方法更适合大量的数据加密,而公钥加密方法用来实现密钥协商。
密码学还为信息安全中除保密性外的其他一些问题提供了解决方案。
1.完整性
数据完整性检验通常是通过密码学中的单向散列函数(Hash函数)来实现的。单向散列函数是将任意长度的输入转化为一个固定大小的消息摘要,表示为:
h:{0,1}*→{0,1}n,m↦h(m)
单向散列函数将任意长度的比特串{0,1}*映射成长度为n的比特串{0,1}n,它具有错误检测的能力,即改变数据的任何一位或者多位,都会导致消息摘要的改变。根据消息m和消息摘要h(m)的对应关系,接收者可以判断消息在传输过程中是否被篡改过。
单向散列函数的目的就是要产生消息的“指纹”,用于认证和数字签名。单向散列函数必须具备单向性,并且能够避免冲突。这就意味着,对于任何给定的消息摘要y,找到满足h(m)=y的消息m在计算上是不可行的。对于任何给定的消息m1,找到满足m1≠m2且h(m1)=h(m2)的m2在计算上是不可行的。找到任何满足h(m1)=h(m2)的数偶(m1,m2)在计算上是不可行的。
美国国家标准技术研究所(National Institute of Standards and Technology,NIST)和一些国际组织不断地制定和颁布单向散列函数标准。1991年美国麻省理工计算机科学实验室(MIT Laboratory for Computer Science)和RSA数据安全公司(RSA Data Security Inc.)的Ronald L.Rivest教授开发出MD5(Message Digest 5)算法。MD5经由MD2、MD3和MD4发展而来,对输入按512位进行分组,并以分组为单位进行处理,输出为128位的数据摘要。1992年美国NIST公布了FIPS PUB 180,通常称之为SHA-0(Secure Hash Algorithm),1995年NIST对SHA-0进行了改进,公布了FIPS PUB 180-1,称为SHA-1。SHA-1对输入按512位进行分组,并以分组为单位进行处理,输出为160位的数据摘要。为了增加单向散列函数的安全性和与加密标准AES配套,2002年NIST公布了SHA的修订版FIPS PUB 180-2,称为SHA-2。SHA-2包含三个单向散列函数,其长度分别为256比特、284比特和512比特,分别称为SHA-256、SHA-284和SHA-512。
例2-4 单向散列函数示例。
hash(‘abc’,‘MD5’)=900150982cd24fb0d6962f7d28e17f72
hash(‘abc’,‘SHA-1’)=a9992e264706816aba2e25717850c26c9cd0d89d
hash(‘abc’,‘SHA-256’)=
ba7816bf8f01cfea414140de5dae2222b00261a296177a9cb410f f61f20015ad
hash(‘abc’,‘SHA-284’)=
cb00752f45a25e8bb5a02d699ac65007272c22ab0eded1621a8b605a42f f5bed8086072ba1 e7cc2258baeca124c825a7
hash(‘abc’,‘SHA-512’)=
ddaf25a192617abacc417249ae20412112e6fa4e89a97ea20a9eeee64b55d29a2192992a27 4f c1a826ba2c22a2 feebbd454d4422642ce80e2a9ac94 fa54ca49 f
2.认证性
为了认证消息的完整性,需要对消息生成某种形式上的鉴别符,通过对鉴别符的分析,可以得知原始消息是否完整。在密码学中,消息加密、消息认证码(Message Authentication Code,MAC)和单向散列函数都是消息认证的重要手段。消息加密是将整个需要认证的消息加密,以加密的结果作为鉴别符。消息认证码是将需要认证的消息通过一个公共函数的作用,以产生的结果和密钥作为鉴别符。单向散列函数是将需要认证的消息通过一个公共函数映射为定长的消息摘要,以消息摘要作为鉴别符。
利用消息认证码对消息进行认证的过程是这样的:发送者Alice利用MAC函数f和密钥k把需要认证的消息m变换成n比特的消息认证码f(k,m),将消息认证码f(k,m)作为鉴别符附加在消息m之后,发送消息序列{m‖f(k,m)}给接收者Bob(如图2-4所示)。接收者Bob收到发送的消息序列{m‖f(k,m)}后,按照与发送者Alice相同的方法对接收的数据m进行计算,应得到相应n比特的消息认证码f(k,m)。如果攻击者Eve篡改了消息m,但是Eve又没有能力计算相应的MAC,接收者Bob接收到的MAC和计算出来的MAC一定是不匹配的,因为MAC计算中需要用到密钥k,在不知道密钥k的情况下,其他人不可能计算出正确的消息认证码f(k,m)。
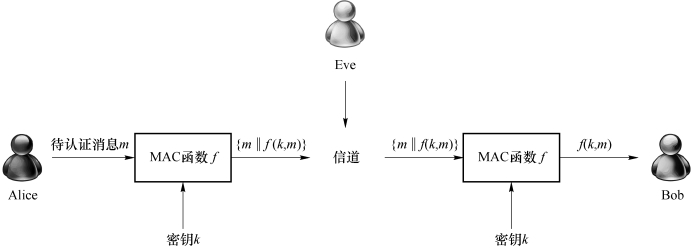
图2-4 利用消息认证码进行认证的过程
实现消息认证码可以有多种方法,基于单向散列函数的消息认证码(Hash-based Message Authentication Code,HMAC)算法是目前广泛使用的一种消息认证码算法。HMAC像单向散列函数算法一样输出一个固定大小的消息标记,但与单向散列函数算法不同的是,HMAC算法需要使用密钥来阻止任何对消息标记的伪造。基于分组密码的消息认证码(Cipher-based Message Authentication Code,CMAC)算法也是目前广泛使用的一种消息认证码算法。公钥算法是实现认证的另一种方法。与HMAC算法和CMAC算法不同的是,基于公钥的认证算法不需要通信双方在通信之前共享私有信息,例如,RSA算法和椭圆曲线DSA(Elliptic Curve Digital Signature Algorithm,ECDSA)标准。
使用什么样的认证方法取决于认证系统的构造。基于公钥的认证方法通常用于通信双方的初始认证。在传输信道安全的情况下,使用HMAC算法和CMAC算法可以提高通信的效率,节省通信的资源。
3.不可否认性
不可否认性通常是通过公钥密码学中的数字签名算法实现的。一方面,数字签名依赖于签名人的私钥,只有签名人才能生成签名;另一方面,任何人都可以利用签名人的公钥和依赖于签名人公钥的公开的验证算法Verify验证签名的有效性(如图2-5所示)。

图2-5 不可否认机制
Alice用自己的私钥kd和签名算法Sign对消息m签名,得到签名
s:=Sign(kd,m)
并把消息m和签名s传送给Bob。Bob接收到消息m和签名s后,用Alice的公钥ke和验证算法Verify检验
Verify(ke,s,m)=ok
是否成立来验证签名是否有效。通常,签名不是对消息本身,而是先用单向散列函数求出消息摘要,然后对消息摘要进行签名。攻击者Eve可以截获签名消息{m‖s},但是,Eve没有签名者Alice的私钥,不能伪造有效的签名。
