5.5.4 DSA数字签名
DSA是ElGamal签名方案的一种演变方案,它由Kravitz提出,被美国国家标准技术研究所在1991年8月提议成为美国联邦信息处理标准(FIPS 186),即数字签名标准(DSS)。DSS的安全性是基于离散对数问题的,DSA是DSS的签名算法。DSA数字签名的原理如图5-4所示。
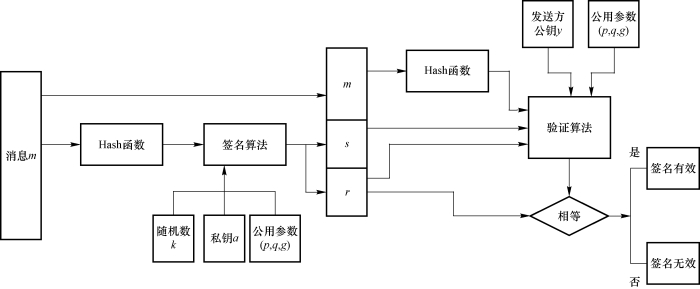
图5-4 DSA数字签名的原理
1.发送方密钥的生成
(1)选择一个大素数q,满足2159<q<2160;
(2)选取t,使得0≤t≤8,并选择素数p满足2511+64t<p<2512+64t,且q整除(p-1);
(3)计算g=h(p-1)/q mod p,其中h是一个整数,1<h<(p-1),且要求h(p-1)/q mod p>1;
(4)随机选择一个数值a,使得1≤a≤q-1,用户的私钥是a;
(5)计算y=ga mod p,用户的公钥是(p,q,g,y)。
2.签名过程
(1)选择一个随机整数k,满足0<k<q,计算r=(gk mod p)mod q;
(2)计算k-1 mod q;
(3)计算s=k-1{h(m)+ar}mod q,则消息m的签名为(r,s)。
3.验证过程
(1)验证者获得发送方的公钥(p,q,g,y),验证0<r<q和0<s<q,否则拒绝该签名;
(2)计算w=s-1 mod q和h(m);
(3)计算u1=wh(m)mod p和u2=rw mod p;
(4)计算v=(gu1 yu2 mod p)mod q,当且仅当v=r时接受签名。
例5-7 利用DSA签名方案完成签名。
发送方密钥的生成过程如下。
(1)发送方选择素数p=124 540 019,q=17 389,满足q整除(p-1);
(2)选择h=110 217 528,计算
g=h7162 mod p=10 083 255
(3)选择随机数a=12 496,满足1≤a≤q-1,计算
y=ga mod p=10 083 25512496 mod 124 540 019=119 946 265
则生成的私钥是a=12 496,公钥是
p=124 540 019,q=17 389,g=10 083 255,y=119 946 265
签名生成过程如下。
(1)选择随机数k=9 557,计算
r=(gk mod p)mod q=(10 083 2559557 mod 124 540 019)mod 17 839
=27 039 929 mod 17 389=34
(2)计算k-1 mod q=7 631,并利用设定好的Hash函数h(m)=5 246;
(3)计算
s=7 631×{5 246+12 496×34}mod q=13 049
则签名为(r=34,s=13 049)。
签名验证过程如下。
(1)接收方计算w=s-1 mod q=1 799;
(2)计算
u1=wh(m)mod p=5 246×1 799 mod 17 839=12 716
和
u2=rw mod p=34×1 799 mod 17 839=8 999
(3)再计算
![]()
因为v=r,所以接受签名。
4.DSA签名的特性及安全性
(1)由于DSA是ElGamal签名方案的一种变体,所以上一节有关ElGamal签名方案的安全性讨论都适用于DSA。
(2)在DSA签名方案中,可以进行指数预运算而不必在签名生成时进行,因为指数运算中的参数与原始消息无关,所以它可在签名前就进行运算,从而减少签名过程耗费的时间。
(3)DSA签名方案是基于两个不同又相关的离散对数问题的,因此想从签名结果推算出发送方的秘密参数是不可能的。
(4)1996年推荐的DSA安全模数至少为768比特,而1 025位的DSA系统具有更高的安全性。
(5)DSA的隐信道最早由Simmons发现,它在签名中可以传递额外的少量信息,因此对于重要的应用,不建议接收由信任度不高的团体利用DSA生成的数字签名。
5.DSA与RSA的区别
(1)DSA虽然是一种公钥密码技术,但它不能用于加密解密,也无法用于密钥分配,因为它是专门设计用作数字签名的;而RSA算法既可以用于加密解密,也可以用于数字签名。
(2)DSA在签名时使用了随机数,因此它是随机化的数字签名,即对于同一个消息每次签名的结果不一样;而RSA是确定性的数字签名,对于同一个消息签名结果相同。
