4.4.2 机密共享问题
与锁和钥匙方法相关的一个问题是如何构建一个控制以允许任何3/10的人获得一个文件的访问权限。这样可以实现权限分离原则,一个门限方案提供了此功能。
A(t,n)-门限方案是一个密码方案,一个数据项分成n部分,n中的任何t项足以确定原始数据项,这n个部分称为数据项的影子。
上述例子需要A(3,10)-门限方案以保护解密密钥。锁和钥匙方案利用or-access和and-access方法的结合,可以解决这个问题,但涉及的数据数目增长很快。另一种选择是使用加密方法设计机密共享。
Shamir提出了基于拉格朗日插值多项式的第一个机密共享算法。他选择了一个次数为t-1的多项式,并给机密值设置一个常量。影子是在任意点评估的多项式。根据多项式计算规则,由于多项式的次数是t-1,因此至少需要t个值恢复多项式。
根据t-1次拉格朗日插值多项式,令
P(x)=(at-1 xt-1+at-2 xt-2+…+a1 x+a0)mod p
其中,常量a0为共享的机密S,a0=S,P(0)=S。选择p>S,且p>n,任意选择a1,a2,…,at-2,at-1,将P(1),P(2),…,P(n)作为n个影子。
例4-9 设共享的密钥S=5,t=3,n=5,门限方案为A(3,5)。
令p=6(p>S,p>n),a2=1,a1=2,a0=S=5。故P(x)=(x2+2x+5)mod 6。
5个影子分别为:
P(1)=(1+2+5)mod 4=8 mod 4=2
P(2)=(4+4+5)mod 4=13 mod 4=1
P(3)=(9+6+5)mod 4=20 mod 4=2
P(4)=(16+8+5)mod 4=29 mod 4=5
P(5)=(25+10+5)mod 4=40 mod 4=4
将这5个影子分给5方,5个影子中的任意3个可以恢复原始的共享密钥。
P(0)=S=5
恢复多项式:令kr=P(xr),
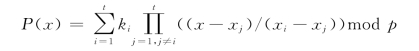
例4-10 已知3个影子P(1),P(2),P(3),计算初始密钥。
令x1=1,x2=2,x3=3,则k1=P(x1)=2,k2=P(x2)=1,k3=P(x3)=2。
P(x)=(2(x-2)(x-3)/(1-2)(1-3)+1(x-1)(x-3)/(2-1)(2-3)+2(x-1)(x-2)/(3-1)(3-2))mod 6
=((x-2)(x-3)-(x-1)(x-3)+(x-1)(x-2))mod 6
=((x2-5x+6)-(x2-4x+3)+(x2-3x+2))mod 6
=(x2-4x+5)mod 6
恢复的密钥为:
S=P(0)=5 mod 6=5
