5.5.1 RSA数字签名
RSA数字签名方案是第一个基于公钥的数字签名方案,也是至今最实际、最通用的一种数字签名技术。RSA方案基于整数因子分解的困难性,它属于确定性的数字签名方案,即对于同一个消息签名结果相同。RSA数字签名的原理如图5-3所示。
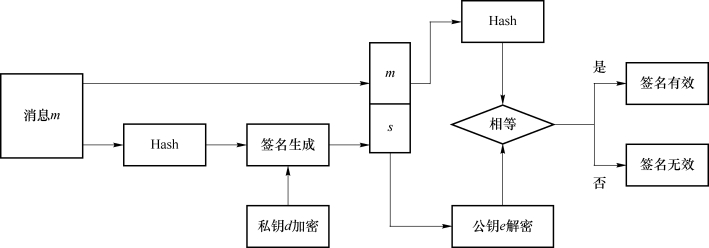
图5-3 RSA数字签名的原理
1.发送方密钥的生成
(1)随机产生两个不同的大素数p和q,计算n=pq和φ(n)=(p-1)(q-1);
(2)随机选择数e,满足1<e<φ(n),且gcd(e,φ(n))=1,那么公钥就是(e,n);
(3)计算d,满足ed=1 modφ(n),私钥就是d。
其中,φn()为Euler函数,φn()=p-1()q-1()。函数gcd表示最大公因子。
2.签名过程
(1)计算h m(),其中h(m)为Hash函数;
(2)计算s=(h(m))d mod n,则s为消息m的签名;
(3)发送(m,s)给接收方。
3.验证过程
(1)取得发送方的公钥(e,n),计算h′=se mod n;
(2)计算消息m的Hash值h m();
(3)若h′=h(m),则签名有效;否则,签名无效。
例5-4 若选择p=7,q=17,则有n=pq=7×17=119,φn()=96,选择公钥参数e=5,
gcd(e,φ(n))=gcd(5,96)=1
计算私钥参数d=77,因为
ed=5×77=4×96+1=1 mod 96
假如消息m=66,简单起见选择h m()=m,则签名为
s=md mod n=6677 mod 119=19
验证
m′=se mod n=195 mod 119=66=m
因此签名有效。
4.RSA签名的安全性
(1)RSA是基于公钥的数字签名,因此加密和解密的速度比较慢,尤其当消息比较长的时候。因此采用Hash函数对消息进行散列运算,然后再对散列值进行签名,可以克服这一缺点。1996年推荐的RSA模长至少为768比特,但是对于重要的签名推荐模长至少是1 025比特。
(2)由于RSA的保密原理是利用整数因子分解,因此如果敌手能够分解发送者的模数n,那么就能计算出φ,最后推导出私钥d,从而造成系统的完全攻破。所以为了RSA的安全性,n应该足够大,但考虑到系统加密的速度,n的长度应该与实际应用相权衡。
(3)RSA的乘法特性也称作同态特性,是由Davida首先发现的。通过乘法特性,攻击者可以在不知道签名者私钥的情况下,伪造出某些消息的有效签名。攻击者可以利用某些冗余函数对原始消息进行变换,再进行签名,以此确保非乘性。而使用冗余函数是签名方案安全性的必要和充分条件。在数字签名的第一个国际规范ISO/IEC 9796中给出了一个标准的冗余函数,其中冗余函数R的定义为:设f(x1~xn)为n变量完全定义的逻辑函数,当且仅当f满足![]() 时,称函数f为冗余函数,变量xi为冗余变量。
时,称函数f为冗余函数,变量xi为冗余变量。
