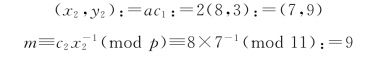2.2.2 基于公钥的加密方法及技术
公钥密码学的基本思想是公开密钥。每一个用户的密钥分为两个部分：一个是任何人都可以使用的加密用的公钥；一个是只有用户本人使用的解密用的私钥。
1.公钥密码学的基本概念
1976年，W.Diffie和M.E.Hellman在他们的论文《密码学的新方向》中提出了公开密钥的思想，设想了一种无须事先传递密钥的密码体制，给出了一种密钥协商的方法，这种方法在公钥密码学中使用至今。
每一个公钥密码体制的用户都拥有一对个人密钥k=（pk，sk），包括公钥pk和私钥sk。公钥pk是公开的，任何用户都可以知道，私钥sk只有拥有者本人知道。Alice和Bob相互发送消息，Alice利用Bob的公钥pk加密明文m，得到密文c：=E（pk，m），并把密文c传送给Bob。Bob利用自己的私钥sk解密密文c，得到明文m：=D（sk，c）（如图2-9所示）。
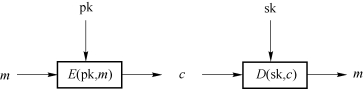
图2-9 公钥密码的工作原理
为了保证公钥密码系统的安全，必须确保从公钥pk计算私钥sk是不可行的，密钥空间足够大，存在有效的算法实现随机选择密钥。公钥密码的安全性取决于某些困难问题的难解性。公钥密码中常用的难解问题有分解大整数问题、离散对数问题、椭圆曲线上的离散对数问题等。
2.RSA
1977年美国麻省理工学院的三位数学家Ron Rivest、Adi Shamir和Len Adleman成功地设计了一种公钥密码算法，该算法根据设计者的名字被命名为RSA算法，在其后的20年中，RSA成为世界上应用最为广泛的公钥密码体制。RSA密码体制的安全性基于大整数分解的困难性。
若已知两个大素数p和q，求n：=pq是容易的，而由n求p和q则是困难的，这就是大整数分解问题。
（1）密钥生成
密钥生成算法执行以下3个步骤：
①选择不同的大素数p和q，计算n：=pq，φ（n）：=（p-1）（q-1）。
②选择e，满足1＜e＜φ（n），且gcd（e，φ（n））=1，（n，e）作为公钥。
③通过ed≡1 modφ（n）计算d，满足e≠d，（n，d）作为私钥。
其中，n、e、d分别为模数、加密指数和解密指数，φ（n）是n的欧拉函数值，d是e在模φ（n）下的乘法逆元。
（2）加密与解密
加密时首先对明文比特串分组，使得每个分组对应的十进制数小于n，即分组长度小于log2n。对{0，…，n-1}范围内的消息m进行加密，考虑消息m为Zn中的一个元素。
加密函数定义如下：
E:Zn→Zn,x↦xe
解密函数定义如下：
D:Zn→Zn,x↦xd
E和D都为双射并且彼此互逆。即，对于任意明文m∈Zn，
加密算法定义如下：
c≡me(mod n)
解密算法定义如下：
m≡cd(mod n)
例2-8 RSA应用示例，Alice向Bob发送加密消息。Bob：选取p：=101，q：=113，计算
n:=pq:=101×113:=11 413
φ(n):=(p-1)(q-1):=100×112:=11 200
选取e：=3 533，验证
gcd(e,φ(n)):=gcd(3 533,11 200)=1
计算
d≡e-1 modφ(n):=3 533-1 mod 11 200:=6 597
Bob公钥（n，e）：=（11 413，3 533），私钥（n，d）：=（11 413，6 597）。
Alice：加密明文m：=9 726，计算
c≡me(mod n):=9 7263533(mod 11 413):=5 761
把密文c=5 761传送给Bob。
Bob：收到密文c=5 761后，计算
m≡cd(mod n):=5 7616597(mod 11 413):=9 726
3.ElGamal
El Gamal密码是1985年由T.ElGamal提出的，是基于离散对数问题的最著名的公钥密码体制。若给定一个大素数p，p-1有一大素数因子，则可构造一个乘法群
是一个p-1阶循环群。设g是
的一个本原根，1＜g＜p-1，若已知x求y：=gx mod p是容易的，而由y、g、p求x，使得y：=gx mod p成立则是困难的，这就是离散对数问题。
（1）密钥生成
密钥生成算法执行以下3个步骤。
①选择大素数p，使p-1有大素数因子，选择
为本原根。
②随机选择整数d，满足1≤d≤p-2，d为私钥。
③计算e≡gd（mod p），e为公钥。
将p、g和e公开，为所有用户所共享，d保密。
（2）加密与解密
对消息
进行加密，随机选择整数k，满足1≤k≤p-2。
加密函数定义如下：
E:Zp→Zp,x↦xek
解密函数定义如下：
D:Zp→Zp,x↦x(gk)-d
即，对于任意明文
，随机整数1≤k≤p-2。
加密算法定义如下：
c1≡gk(mod p)
c2≡mek(mod p)≡mgdk(mod p)
解密算法定义如下：
m≡c2(c1)-d(mod p)≡mgdk(gk)-d(mod p)
加密结果依赖于消息m、公钥e和随机整数k。如果随机整数k的选择与消息m无关，那么几乎不可能出现两个明文生成同一个密文的情况。
例2-9 ElGamal应用示例，Alice向Bob发送加密消息。
Bob：选取素数
上的本原根g：=2，私钥d：=1 751，计算
e≡gd(mod p):=21751(mod 2 357):=1 185
e=1 185为Bob公钥。
Alice：加密明文m：=2 035，随机选取整数k：=1 520，计算
c1≡gk(mod p)≡21520(mod 2 357):=1 430
c2≡mek(mod p)≡2 035×1 1851520(mod 2 357):=697
将密文（c1，c2）：=（1 430，697）传送给Bob。
Bob：收到密文（c1，c2）：=（1 430，697）后，计算
4.ECC
1985年，Koblitz和Miller分别提出利用椭圆曲线来开发公钥密码体制。椭圆曲线密码（Elliptic Curve Cryptography，ECC）的安全性基于椭圆曲线离散对数求解的困难性。目前普遍认为，椭圆曲线离散对数问题要比大整数因子分解和有限域上的离散对数问题难解得多。
椭圆曲线是满足一类方程的点的集合，通过在点间定义一种特殊的运算，可以得到一个群，称为椭圆曲线群。设E是某有限域上的椭圆曲线（群），G是E的一个素数阶循环子群，α是G的一个生成元，β∈G。已知α和β，求满足nα=β的唯一整数n，称为椭圆曲线上的离散对数问题。
与RSA密码相比，ECC密码能用较短的密钥实现较高的安全性。就是说，要达到同样的安全强度，ECC算法所需的密钥长度远比RSA算法短，并且随着加密强度的提高，ECC的密钥长度变化不大（如表2-4所示）。
表2-4 RSA和ECC的性能比较
注：MIPS年指以MIPS（Millions of Instructions Per Second，CPU的速度达到每秒执行百万条指令）级的计算机来运算，所需的攻破时间。
设p是一个大于2的素数，Fp是模p的有限域，Fp上的椭圆曲线E定义为
E:y2≡x3+ax+b(mod p)
其中，a，b，x，y∈Fp且满足
4a2+27b3≠0(mod p)
E（Fp）表示曲线E上的所有点（x，y）和无穷远点O的集合，也记为Ep（a，b），或者直接记为E。
在椭圆曲线E上按如下法则定义加法运算。
（1）定义无穷远点O为加法单位元，对于任意点P∈E有
P+O:=O+P:=P
（2）若P：=（x，y）∈E，定义-P：=（x，-y），（x，y）+（x，-y）：=O。
（3）若P：=（x1，y1）∈E，Q：=（x2，y2）∈E，定义P+Q：=（x3，y3），其中，
例2-10 设a：=1，b：=6，p：=11，椭圆曲线方程为
E:y2≡x3+x+6(mod 11)
计算E11（1，6）：=
{O,(2,4),(2,7),(3,5),(3,6),(5,2),(5,9),(7,2),(7,9),(8,3),(8,8),(10,2),(10,9)}
设P：=（2，7），计算
x3:=82-2-2(mod 11):=5
y3:=8×(2-5)-7(mod 11):=2
那么，可以算出
P:=(2,7),2P:=(5,2),3P:=(8,3),4P:=(10,2),5P:=(3,6),6P:=(7,9),7P:=(7,2),8P:=(3,5),9P:=(10,9),10P:=(8,8),11P:=(5,9),12P:=(2,4),13P:=O
结果表明：椭圆曲线E有12个点，E11（1，6）是一个循环群，P=（2，7）是椭圆曲线E的生成元。任意素数阶的群是循环群，任何非无穷远点都是E的生成元。
椭圆曲线上的公钥密码有两种方案。
方案1：将明文m编码为椭圆曲线上的点Pm：=（xm，ym）。
（1）密钥生成
在椭圆曲线Ep（a，b）上选取大的素数阶n，生成元为P，Alice和Bob共享椭圆曲线的公共参数。Bob随机选取整数a，满足1≤a≤n-1，计算Q：=a P，Bob公钥为Q，私钥为a。
（2）加密
Alice首先将明文m编码为椭圆曲线Ep（a，b）上的点Pm：=（xm，ym），然后随机选取整数k，满足1≤k≤n-1，计算
c1:=k P:=(x1,y1)
c2:=Pm+kQ:=(x2,y2)
得到密文为（c1，c2）。
（3）解密
Bob收到密文（c1，c2）后，计算
Pm:=c2-ac1
再对Pm解码得到明文m。
方案2：将明文m限定为m∈Fp。
（1）密钥生成
密钥生成算法同方案1。
（2）加密
Alice随机选取整数k，满足1≤k≤n-1，计算
(x2,y2):=kQ
直到x2≠0，计算
c1:=k P:=(x1,y1)
c2≡mx2(mod p)
得到密文为（c1，c2）。
（3）解密
Bob收到密文（c1，c2）后，计算
(x2,y2):=ac1
然后计算
得到明文m。
例2-11 设有限域F11上的椭圆曲线
E:y2=x3+x+6
所有的点关于加法构成循环群，P：=（2，7）是生成元。
（1）密钥生成
Bob随机选取私钥a：=2，计算公钥Q：=a P：=2（2，7）：=（5，2）。
（2）加密
Alice要将明文m：=9，m∈F11加密传送给Bob，随机选取k：=3，计算
c1:=k P:=3(2,7):=(8,3)
k Q:=3(5,2):=(7,9)
c2≡mx2(mod p)≡9×7(mod 11):=8
Alice将密文（c1，c2）：=（8，3，8）传送给Bob。
（3）解密
Bob收到密文（c1，c2）：=（8，3，8）后，计算
