2.2.1 关系的数学定义
1)域(Domain)
【定义2.1】 域是一组具有相同类型的值的集合,一般用大写字母D表示。
例如,自然数、整数、小数、长度小于20字节的字符串集合、{男,女}都可以是域。
2)笛卡尔积(Cartesina Product)
【定义2.2】 给定一组域D1,D2,…,Dn,这些域可以有相同的,那么D1,D2,…,Dn的笛卡尔积为:
![]()
其中每一个元素(d1,d2,…,dn)叫作一个n元组,简称元组,元组中的每一个值di叫作分量。若Di(i=1,2,…,n)为有限集,其基数为mi(i=1,2,…,n),则D1×D2×…Dn的基数M为:![]()
因此,笛卡尔积可以表示成一个形式化的二维表,表中的每行对应一个元组,表中的每列对应一个域。例如,给出如下3个域:
D1=导师集合={张老师,李老师}
D2=专业集合={计算机专业,大数据专业}
则D1,D2,D3的笛卡尔积为:D1×D2×D3={(张老师,计算机专业,张同学),(张老师,计算机专业,王同学),(张老师,计算机专业,孙同学),(张老师,大数据专业,张同学),(张老师,大数据专业,王同学),(张老师,大数据专业,孙同学),(李老师,计算机专业,张同学),(李老师,计算机专业,王同学),(李老师,计算机专业,孙同学),(李老师,大数据专业,张同学),(李老师,大数据专业,王同学),(李老师,大数据专业,孙同学)}
其中,(张老师,大数据专业,张同学)、(李老师,大数据专业,王同学),(张老师,大数据专业,孙同学)等都是元组。张老师、计算机专业、孙同学等都是分量。
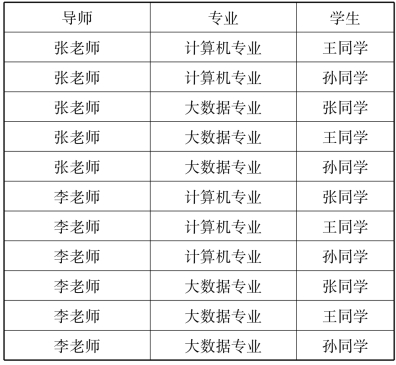
该笛卡尔积的基数是2×2×3=12,也就是说D1×D2×D3一共有2×2×3=12个元组。这12个元组可以构成一张二维表,见表2-4。
表2-4 D1、D2、D3的笛卡尔积

续表
3)关系(Relation)
【定义2.3】 D1×D2×…Dn的子集称为D1,D2,…,Dn上的关系,表示为R(D1,D2,…,Dn)。(https://www.daowen.com)
这里的R表示关系的名字。
关系中涉及的概念如下:
(1)元组与属性
关系是笛卡尔积的一个子集,所以关系从形式上看是一个二维表,表中的每行对应一个元组,表中的每列对应一个域。由于域可以相同,为了加以区分,必须给每列起一个名字,成为属性,表2-4中的“导师”“专业”“学生”都是属性。
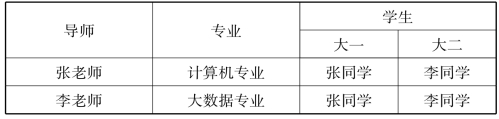
例如,可以在表2-4中的笛卡尔积中取出一个子集构造一个关系,可以得到表2-5的关系。假定现实世界中有语义约束:一个学生只能师从一个导师、学习一个专业,这样,表2-5中的许多元组是没有实际意义。所以在具体的应用中,关系中的元组一定是有实际意义的,满足现实世界语义约束的。
表2-5 D1,D2,D3笛卡尔积的子集构造的关系
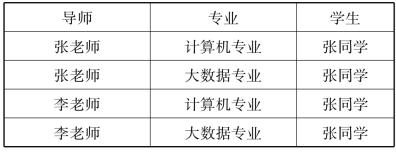
(2)候选码与主码
若关系中的某一个或一组属性能唯一标识一个元组,则称该属性或者属性组为码或者候选码;若一个关系有多个候选码,则选定其中的一个作为主码,主码对应的属性称为主属性,不包含在任何候选码中的属性称为非主属性。在最简单的情况下,候选码只包含一个属性,在最极端的情况下,关系的所有属性是这个关系的候选码,称为全码。如表2-4中的候选码只能是全码。
(3)关系的性质
按照定义2,关系可以是一个无限集合。由于笛卡尔积不满足交换律,所以按照数学定义,(d1,d2,…,dn)≠(d2,d1,…,dn)。当关系作为关系数据模型的数据结构时,必须给予如下限定和扩充:
无限关系在数据库系统中是无意义的,因此,限定关系数据模型中的关系必须是有限集合;
通过为关系的每列附加一个属性名的方式取消这种有序性,即(d1,d2,…,di,dj,…dn)=(d1,d2,…,dj,di,…dn)。
因此,关系具有以下6条基本性质:
①列是同质的,即每一列中的分量是同一类型数据,来自同一个域;
②不同的列可以出自同一个域,要用不同的属性名加以区分;
③列的顺序无所谓,可以任意交换;
④行的顺序无所谓,可以任意交换;
⑤任意两个元组不能完全相同;
⑥关系中的每一个分量必须取原子值,即每个分量都是不可再分的数据项。
表2-6所示的例子就是不满足基本性质⑥的关系。
表2-6 不满足基本性质的关系