2.4.1 传统的集合运算
从数学的角度看，关系是一个集合，因此，传统的集合运算是将元组作为集合中的元素进行运算，其运算是从关系的水平方向（行的角度）进行的，包括并、交、差和笛卡尔积运算。
（1）并运算
设关系R和关系S具有相同的目n（即两个关系都有n个属性），并且对应的属性取自同一个域，则：关系R和关系S的集合并运算可以记为：
。
其中，∪为并运算符，t为关系R或关系S的元组变量，∨为逻辑或运算符，因此可知：关系R和关系S并运算的结果是仍为n目关系，由属于R或者属于S的元组组成的集合。如果R和S中有重复的元组，根据关系的性质，只保留一个。并运算主要用于关系数据的增加操作。
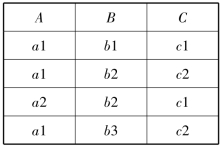
【例2.2】 若关系R和关系S见表2-8、表2-9，则R和S并运算结果见表2-10。
表2-8 关系R
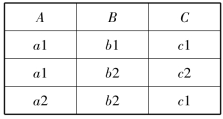
表2-9 关系S
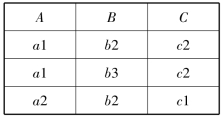
表2-10 关系R∪S
（2）交运算
设关系R和关系S具有相同的目n（即两个关系都有n个属性），并且对应的属性取自同一个域，则关系R和关系S的集合交运算可以记为：
。
其中，∩为交运算符，t为关系R或关系S的元组变量，∧为逻辑与运算符，因此可知：关系R和关系S交运算的结果是仍为n目关系，由属于R并且属于S的元组组成的集合。
【例2.3】 若关系R和关系S见表2-8、表2-9，则R和S交运算结果见表2-11。
表2-11 关系R∩S
（3）差运算
设关系R和关系S具有相同的目n（即两个关系都有n个属性），并且对应的属性取自同一个域，则关系R和关系S的集合差运算可以记为：
。
其中，-为差运算符，t为元组变量，∧为逻辑与运算符，因此可知：关系R和关系S差运算的结果是仍为n目关系，由属于R但不属于S的元组组成的集合。差运算主要用于关系数据的删除操作。
对于关系数据的修改操作，可以看作是并运算和差运算的组合运算。假设修改关系R内某个元组的内容，可以用下面的方法实现：首先假设需要修改的元组构成关系R1，则先做删除，得到R-R1；其次设修改后的元组构成关系R2。此时将其插入，得到结果（R-R1）∪R2。
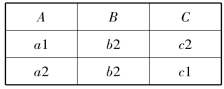
【例2.4】 若关系R和关系S见表2-8、2-9，则R和S差运算的结果见表2-12。
表2-12 关系R-S
交运算和差运算之间存在如下关系：R∩S=R-（R-S）=S-（S-R）。
设关系R中有i个元组，关系S中有j个元组，两者有k个相同的元组，则R∩S中的元组数为k，R∪S中的元组数为i+j-k，R-S中的元组数为i-k。
（4）笛卡尔积运算
两个分别为m目和n目的关系R和S的笛卡尔积（Cartesian Product）是一个有（m+n）个属性的元组的集合，元组的前m列是关系R中的一个元组，后n列是关系S的一个元组。若R有i个元组，S有j个元组，则关系R和关系S的笛卡尔积有i×j个元组。记作：
其中，“×”为笛卡尔积运算符，＜tm，tn＞表示笛卡尔积运算所得到的新关系的元组是由两部分组成的有序结构，tm表示由含有关系R的属性的元组构成，tn表示由含有关系S的属性的元组构成。
说明：
①上述的表示中，虽然把关系R的属性放在前面，把关系S的属性放在后面，连接成一个有序结构的元组；但在实际的关系操作中，属性间的前后顺序是无关的。
②在做笛卡尔积运算时，可以从R的第一个元组开始，与S的每一个元组依次组合成一个有序结构，然后对R的下一个元组进行同样的操作，直到R的最后一个元组也进行完同样的操作为止，即可得到笛卡尔积运算的全部结果。
③通过笛卡尔积操作可以实现关系之间的连接操作。笛卡尔积运算得出的新关系可以将数据库的多个孤立的关系联系在一起，这样使关系数据库中孤立的关系之间有了沟通的渠道。
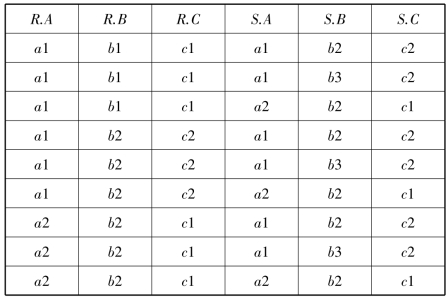
【例2.5】 若关系R和关系S见表2-8、表2-9，则R和S笛卡尔积运算的结果见表2-13。
表2-13 关系R×S
笛卡尔积运算在理论上要求参加运算的关系没有同名属性。如果有同名属性，通常在结果关系的属性名前面加上“关系名”来进行区分，这样，即使关系R和关系S中有同名属性，也能保证结果关系中属性名的唯一性。