2.4.2 专门的关系运算
和传统的关系运算不同，专门的关系运算不仅涉及关系的行，而且涉及关系的列，以便于实现关系数据库多样的查询条件。
（1）选择运算
选择运算是根据给定的条件对关系进行水平分解，选择出符合条件的元组。选择条件用F表示。例如，在关系R中找出满足条件F的所有元组，组成一个新的关系，这个新的关系是关系R的一个子集，记作：
σF（R）＝｛t｜t∈R∧F（t）＝true｝
其中，σ为选择运算符，F为选择条件，R为关系名，t为元组变量，∧为逻辑与运算符。F的形式是由算术运算符和逻辑运算符连接起来的逻辑表达式，取值为“true”或“false”，只有取值为“true”的元组才会被选择。
选择运算是单目运算符，即运算的对象只有一个关系。选择运算不会改变参与运算的关系模式，它只是根据给定的逻辑条件从所给定的关系中找出符合条件的元组。选择运算本质上是从行的角度进行的水平分解运算，是一种将大关系分解成小关系的运算，如图2-12所示。
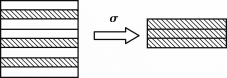
图2-12 选择运算
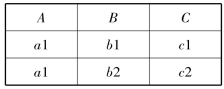
【例2.6】 设关系R（表2-8），从关系R中选择满足A=a1条件的元组，对应的关系代数式为
，其结果见表2-14。
表2-14 选择运算
（2）投影运算
投影运算是从一个关系中选择某些感兴趣的属性列，并对这些属性列重新排列，最后从得出的结果中删除重复的元组，从而构成一个新的关系。
设关系R为n目关系，Ai1，Ai2，…，Aim（m≤n）是R的第i1，i2，…，im个属性，且i1，i2，…，im为1到m之间互不相同的整数，可不连续，则关系R在Ai1，Ai2，…，Aim上的投影定义为：
其中，π为投影运算符，R为关系名，t为元组变量，∧为逻辑与运算符。投影运算表示按照i1，i2，…，im的顺序从关系R中取出所有的元组在指定属性列Ai1，Ai2，…，Aim上的值，并删除结果中的重复元组，构成一个以i1，i2，…，im为列顺序的m目关系。
投影运算也是单目运算符，它是从列的角度进行的垂直分解运算，可改变关系中列的顺序，如图2-13所示。投影运算的结果不仅删除了原关系中的某些列，而且可能删除某些元组，删除了某些列以后会产生重复行，根据关系的基本性质，也应该删除这些重复行。与选择运算一样，投影运算也是一种分解关系的运算。
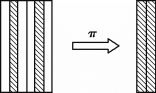
图2-13 投影运算
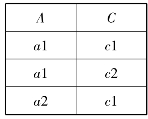
【例2.7】 设关系R（表2-8），计算πA，C（R）或π1，3（R）的结果见表2-15。
表2-15 投影运算
（3）连接运算
连接运算是从两个关系R和S的笛卡尔积中，选取R的A属性值和S的B属性值之间满足一定条件的元组，这些元组构成的关系是R×S的一个子集，记作：
其中，A和B分别为R和S上可比的属性名（属性名可以不相同），定义在同一个域上，θ为比较运算符，可以是＜、≤、≥、＞、=、≠。
【例2.8】 设有关系R（表2-16）和关系S（表2-17），计算
。
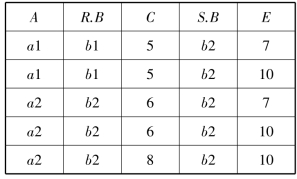
思路：从关系R和关系S的笛卡尔积运算结果中，找出R.C＜S.E的元组，其结果见表2-18。
表2-16 关系R
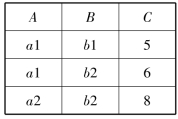
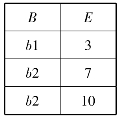
表2-17 关系S
表2-18 
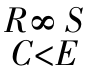运算的结果
在连接运算中包括两种最常用也最重要的运算，分别是等值连接和自然连接。
等值连接：当连接表达式AθB中的比较运算符θ取“=”时的连接运算就称为等值连接，也就是说等值连接是从两个关系的笛卡尔积运算中选取A、B属性集间存在相等关系的元组，记作：
【例2.9】 设有关系R（表2-8）和关系S（表2-9），计算
。
思路：从关系R和关系S的笛卡尔积运算结果中（图2-14）找出R.B=S.B的元组，其结果见表2-19。
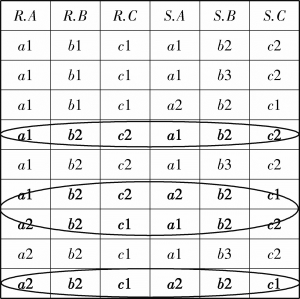
图2-14 关系R×S
表2-19 等值连接运算
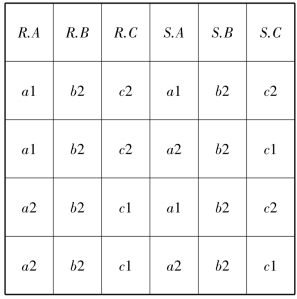
例2.9就是一个等值连接的例子。
自然连接：自然连接是一种特殊的等值连接，它是在等值连接的基础上，去掉结果中重复的属性列。
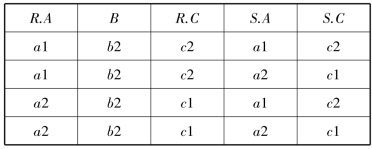
【例2.10】 设有关系R（表2-8）和关系S（表2-9），则R和S自然连接的结果见表2-20（去掉重复的属性列）。
表2-20 自然连接运算
（4）除运算
除运算实际上是笛卡尔积的逆运算，是同时从行和列角度进行的运算。给定关系R（X，Y）和关系S（Y，Z），其中X、Y、Z为属性集合。R中的Y和S中的Y可以有不同的属性名，但必须出自相同的域，则除运算R÷S是满足下列条件的最大关系：其中每个元组t与S中的各个元组s组成的新元组＜t，s＞必在R中。其定义形式为：
从上述定义形式中可以看出，除运算的计算过程如下：
①计算R在属性X上的投影H=πX（R）；
②计算关系H与关系S的笛卡尔积，并与关系R进行差运算得到关系W，即W=H×S-R；
③计算关系W在属性X上的投影K，即K=πX（W）
④最后计算H-K，得到最终结果。
【例2.11】 设有关系R（表2-21）和关系S（表2-22），计算R÷S。
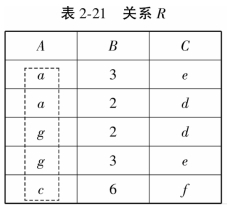
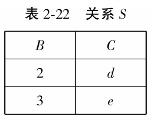
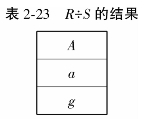
思路：Y=｛B，C｝，X=｛A｝，Z=｛｝；H=πX（R）为表2-21中的虚线部分；通过计算关系H与关系S的笛卡尔积，并与关系R进行差运算得到关系W=｛c，2，d｝；计算关系W在属性X上的投影K，即K=｛c｝；最后计算H-K，得到R÷S，其结果见表2-23。
关系的除运算需要说明的是：
①R÷S得到的新关系属性是由属于R但不属于S的所有属性组成。
②R÷S的任一元组都是R中某元组的一部分，但必须符合下列要求：即任取属于R÷S的一个元组t，则t与S的任一元组相连后，结果都为R中的一个元组。