4.4.3　第四范式——4NF

4.4.3　第四范式——4NF

【定义4.13】　关系模式R∈1NF，对于R（U）中的任意两个属性子集X和Y，如果非平凡的多值依赖，则X含有码，则称R（U）满足第四范式，记为R（U）∈4NF。

关系模式R（U）上的函数依赖X→Y可以看作多值依赖X→→Y，如果R（U）属于第四范式，此时X就是超键，所以X→Y满足BCNF。因此，由4NF的定义，就可以得到下面两点基本结论：

①4NF中可能的多值依赖都是非平凡的多值依赖。

②4NF中所有的函数依赖都满足BCNF。

因此，可以粗略地说，R（U）满足第四范式必满足BC范式。但是反之是不成立的，所以BC范式不一定就是第四范式。

在例4.3中，关系模式CTB唯一的侯选键是｛C，T，B｝，并且没有非主属性，当然就没有非主属性对候选键的部分函数依赖和传递函数依赖，所以CTB满足BC范式。但在多值依赖C→→T和C→→B中的“C”不是键，所以CTB不属于4NF。对CTB进行分解，得到CT和CB（表4-11、表4-12）。

表4-11　关系CT

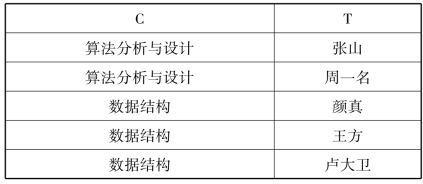
表4-12　关系CB

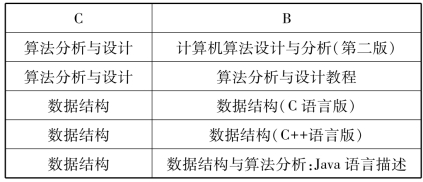
在CT中，有C→→T，不存在非平凡多值依赖，所以CT属于4NF；同理，CB也属于4NF。