◆奇结点图形

下面，我们再来看一下有两个奇结点的图形。

就拿图形（b）来说吧！从图中可以看出，它有两个奇结点，分别是点A和点B。

试一下就会知道，这个图形也可以用一笔画出来。

实际上，从其中的一个奇结点开始，经过某几条线到达第二个奇结点，比如从图形（b）中的点A经过ACB到点B。画完这些线后，对每个奇结点来说，就减少了一条线，就好像这条线不存在似的。所以，这两个奇结点就变成了偶结点。在这个图形中，没有其他的奇结点，所以，现在的图形就只有偶结点了。比如说，在图形（b）中，画完ACB后，就只剩下一个三角形和一个圆周。

这样的图形可以用一笔画下来，所以整个图形也完全可以用一笔画下来。

需要说明的是，当我们从其中的一个奇结点开始画时，必须选择好通往第二个奇结点的路径，不能出现跟原来的图形隔绝的情况。比如说，当我们画图形（b）时，如果你从奇结点A沿直线AB到达另一个奇结点B，那就不行了。因为这时候的圆跟其他部分隔绝开了，下面的图形就画不出来了。

总之，如果在一个图形中有两个奇结点，要想一笔画成功，必须从其中的一个奇结点开始，最终停在另一个奇结点上。也就是说，起点跟终点不在同一个点上。

我们可以很容易得出，如果一个图形有四个奇结点，那它只能用两笔画出，而不是一笔。在图33中，图形（d）和图形（e）都属于这一类。

现在，我们已经看到，如果学会正确思考问题，就可以事先知道很多事情，避免浪费精力和时间。以后遇到此类题目，你可以马上断定，这个图形能否一笔画出来。而且，你还知道应该从哪一个结点开始画。

另外，你也可以自己设计出一些这样的图形让你的朋友解答。

最后，请读者朋友把图34中的两个图形用一笔画出来。

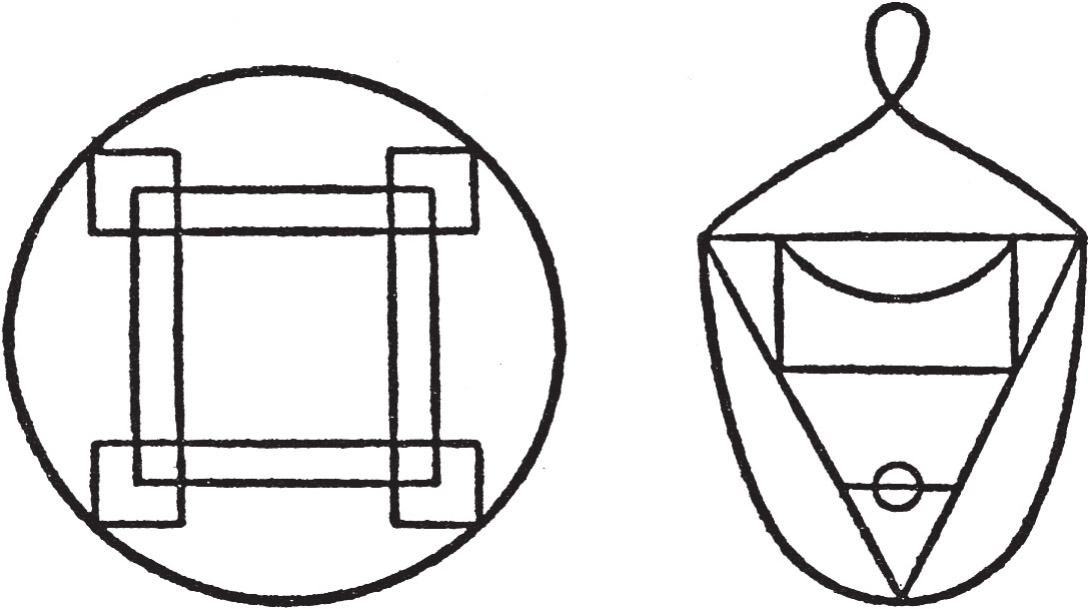
图34