5.1.1 锂离子电池管理与控制方法
锂电池的管理与控制主要包括电池组的保护、单体的均衡、电池状态监测等。
5.1.1.1 电池组的保护方法
该功能主要是对电池组在使用过程中发生的过电压、过电流、短路、欠压、过热等状态进行保护。其主要思路比较简单:当发生过流、短路或过热时,断开电路;当发生过压时,只允许放电,不允许充电;当发生欠压时,只允许充电,不允许放电。具体实现原理如图5-1所示,图中的SDA、SCL、GPIO为协议。其功能如下:
(1)电池状态检测。采用电流采样电阻对充放电过程的电流进行监测,采用热敏电阻对锂电池进行接触式温度监测,电池组中的每片电池均与模拟前端(AFE)集成电路相连,从而获得单片电压状态。
(2)电池保护执行。采用背靠背的场效应管MOSFET来实现电路的定向开关。
(3)控制信号产生。采用模拟前端集成电路配合主控单元实现。当检测到电池处于过流、短路、过热状态时,主控单元通过指令控制AFE关闭Q 1和Q 2,使电路无法进行充放电;当检测到电池处于欠压状态时,主控单元通过指令控制AFE关闭Q 1、打开Q 2,此时电路只允许充电,不允许放电;当检测到电池处于过压状态时,主控单元通过指令控制AFE关闭Q2,打开Q1,此时电路只允许放电,不允许充电。
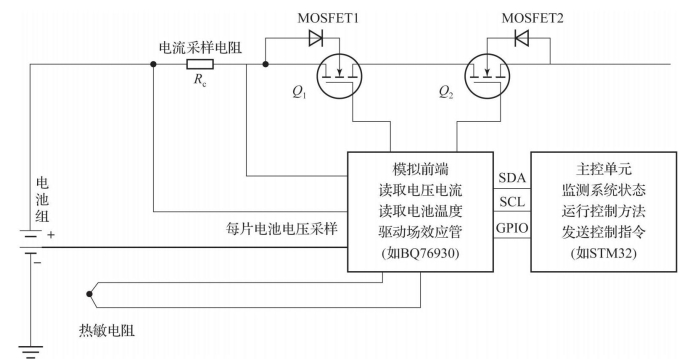
图5-1 锂电池组保护电路
5.1.1.2 单体均衡管理方法
单体电池均衡管理的目的是控制各个单体电池均衡充放电,使电池组中各个单体的电压或当前剩余电量SOC保持基本一致的状态。良好的均衡技术可以延长电池寿命,提高电池效率。电池均衡类型分为被动均衡和主动均衡两种,其主要区别:被动均衡采用“截长不补短”的思想,使用电阻对高能单体进行能量耗散,以追求与其他低能单体的一致性;主动均衡采用“截长补短”的思想,通过能量转移的方式,使电量高的单体向电量低的单体转移部分能量,进而实现各单体之间的一致性。
1.被动均衡控制方法
被动均衡是一种能量消耗型均衡,被动均衡控制方法依托于开关电阻分流电路,如图5-2所示。为每个单体并联一个耗散电阻和一个开关,主控单元配合模拟前端巡检电压过高的单体;发送控制指令将对应的开关闭合,在电压过高的单体和其并联的电阻之间形成回路,以热量的形式将多余电量耗散,达到各个单体电压一致的效果。
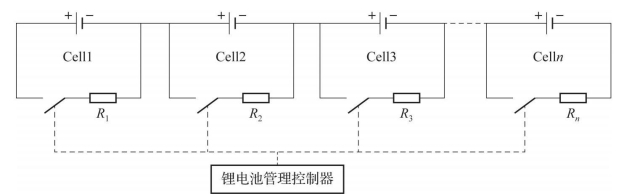
图5-2 开关电阻分流均衡电路
被动均衡电路的优势在于,电路结构简单、成本较低,且控制简单,易于实现。其主要缺点是:能量消耗大,产热明显,会造成能量的浪费;均衡电流通常较小,一般在0.5~1 A,均衡能力有限。当均衡能力要求更高时,通常采用主动均衡控制方法。
2.主动均衡控制方法
主动均衡控制方式主要包括电容式均衡、电感式均衡、变压器式均衡。将这三种方式相比,电感式的能量均衡效率高,电容式和变压器式的能量均衡效率较低;与电容式和电感式相比,变压器式的均衡控制更难。
电容式均衡的思路:将电容作为能量传输介质,对各单体之间进行均衡。当需要对电池组进行均衡时,首先通过控制开关将高电压单体与电容并联,电容放电,把电量转移到并联的电容中;然后,通过控制开关将充电后的电容与低压单体并联,电容放电,将电量转移到低压单体中。由于电容并不消耗能量,因此可以实现能量的无损转移。图5-3是典型电容式均衡的电路示意图。电容均衡电路是依靠单体电池间的电压差实现电量转移,当电压差较大时,可以很快缩小压差实现均衡,但如果电压差较小,则能量转移效果较差。此外,电容需要同时控制两个开关,要求开关双向可控,这增加了控制难度和电路复杂度。
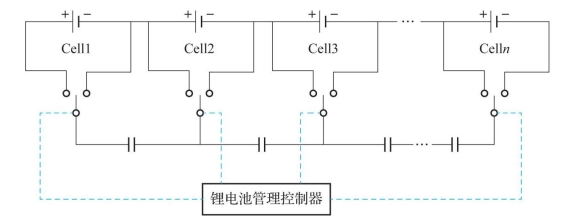
图5-3 典型电容式均衡的电路示意图
电感式均衡的思路:将电感作为能量传输介质,以电流的形式在电感中传递,实现单体之间的均衡。在对电池组进行均衡时,首先通过控制开关将高电压单体与电感并联,并为电感充电,把电量转移到并联的电感中;然后,通过控制开关将充电后的电感与低电压单体并联,电感放电,将电量转移到低电压单体中。图5-4所示为一种电感式均衡的电路示意图。电感均衡电路是以电流的方式转移能量,不依赖于电池电压而补偿电池内部电阻,能够提高均衡电流,且仅需要控制一个单向开关,控制较为简单,但其易引入一些附加的纹波电流,且由于存在开关损耗,电流的分布趋向于高度集中在相邻的电池中。
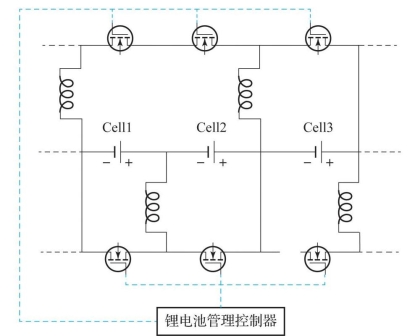
图5-4 电感式均衡的电路示意图
5.1.1.3 电池状态监测方法
电池荷电状态(SOC)的精确估算不仅能使用户安全地使用电器产品,还能在混合能源控制时,合理地根据剩余电量进行状态分配,因此精确估算电池的SOC是非常重要的。SOC的计算公式如下:
![]()
式中,Q c——某时刻电池的剩余可用电量;
Q n——电池的额定容量。
早期的SOC的估算方法主要有放电实验法、开路电压法、安时积分法、内阻法、线性模型法等。进入21世纪以后,出现了卡尔曼滤波法、神经网络法等。近年来,由于卡尔曼滤波法不仅能对SOC进行估算,还能对SOC的误差进行估算,因而备受业界关注。图5-5所示为常用SOC估算方法的分类。
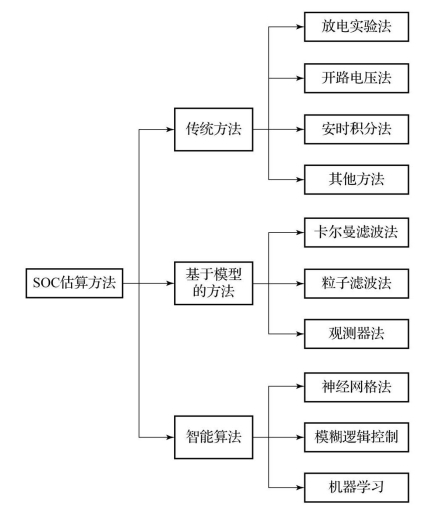
图5-5 常用SOC估算方法的分类
1.放电实验法
放电实验法是以恒定的电流对电池进行放电实验,将电流和放电时间的乘积作为电池的放电量,从而对电池剩余电量进行计算,这是最简单的SOC估算方法。
放电实验法操作简单,估算精度较高。但是,该方法需要耗费大量时间进行测量;而且,电池必须处于脱机状态进行测量,无法带负载测量,不能用于在线估算,因此无法满足实时估算要求。
2.开路电压法
开路电压法是指基于锂电池的开路电压(open circuit voltage,OCV)与SOC存在一定的函数关系,经过多次测量电池不同开路电压和对应的SOC,得到电池的SOC-OCV曲线。实际应用中,先测量电池的OCV,再基于SOC-OCV曲线,进而实现SOC估算。
假定SOC与OCV的关系符合三次函数关系,那么就可以假设其关系为
![]()
然后,根据测量到的(OCV,SOC)数据点进行拟合,即可求出参数a、b、c、d的最优解。(https://www.daowen.com)
开路电压法主要依靠对电池开路电压的测量,但开路电压需要电池长时间充分静置后才能精确测量得到,且开路电压受温度影响大,温度越低,开路电压就越低,因此这种估算方法实时性较差,不能够在线测量,无法满足实时估算要求。
3.安时积分法
安时积分法是指通过实时采集、记录电池充放电过程中的电流,并对其进行积分,从而得到电池充放电的电量值。图5-6所示为安时积分法的SOC估算流程,具体估算公式为
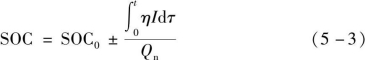
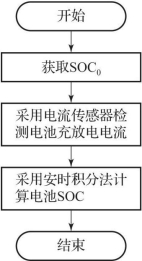
图5-6 安时积分法的SOC估算流程
式中,SOC0——电池的初始电量值;
η——电池的充放电效率系数;
I——电池的充放电电流;
t——充放电时间;
Qn——电池的初始总电量。
安时积分法可以实时计算电池的SOC,适用于全部类型的电池。但是,如果BMS在电流采集过程中出现测量误差,该方法没有反馈校正环节,会使SOC估计值的精确度大大降低。
4.卡尔曼滤波法
卡尔曼滤波法是将电池的SOC和极化电压作为系统的状态变量,将工作电压作为系统的观测变量,建立状态方程和观测方程,采用卡尔曼滤波算法(Kalman filter,KF)对电池SOC进行估计。
卡尔曼滤波状态方程和观测方程如下:

式中,Xk——k时刻的状态;
Yk——k时刻的测量值;
Uk——控制向量;
Wk——状态噪声;
Vk——测量噪声。
卡尔曼滤波法SOC估算流程如图5-7所示,其核心问题是对变量的最小方差做出最优估计。
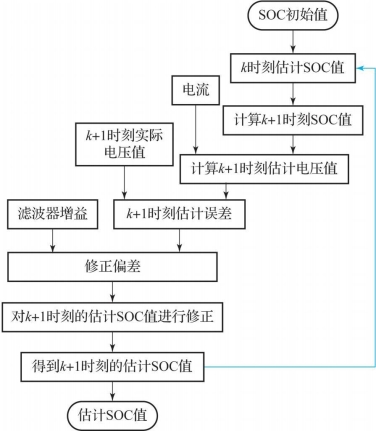
图5-7 卡尔曼滤波法SOC估算流程
以一阶电池电路模型为例(图5-8),其中R 0为电池内阻,R 1为电池的极化电阻,C 1为电池的极化电容。
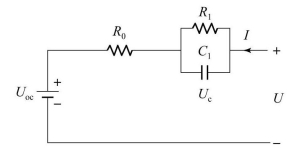
图5-8 一阶电池电路模型
其估算公式如下:
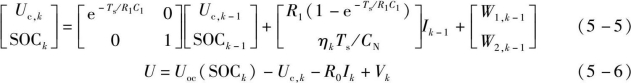
式中,ηk——库伦效率;
C N——电芯容量;
Ts——计算周期;
W1,k-1,W2,k-1——系统噪声;
U——电池端电压;
Uoc(SOCk)——电池开路电压,其与SOC相关;
Vk——观测噪声。
基于式(5-5)和式(5-6),就可以采用图5-7所示的估算流程,完成电池SOC的估算。
卡尔曼滤波法解决了电流不稳定导致的SOC估算误差的问题,其估算精度较高,但其估算精度取决于电池模型的准确程度,并与处理器的运行速度有关。
5.神经网络法
神经网络法是基于模拟人类大脑神经元的工作状态而建立的一套处理输入数据的神经网络系统模型的方法。针对电池在使用过程中,其电流与电压的关系为非线性状态,并且其SOC不能实时计算及自适应优化计算等问题,可以采用神经网络法对SOC进行估算,图5-9所示为基于神经网络法的SOC估算流程。

图5-9 基于神经网络法的SOC估算流程
神经网络法能极大地提高估算的准确性,并可以实现实时SOC估算。但它对建模数据的规模和精度要求比较高,依赖大量的测量数据;同时,其网络训练过程的运算复杂,且成本较高,这在一定程度上制约了其发展和使用。
总结以上SOC估算方法,进行优缺点分析,如表5-1所示。
表5-1 SOC估算方法对比

