7.1.1 飞行状态耦合的电池模型
7.1.1.1 机翼上表面辐照模型
为了简化分析,本书忽略了无人机机翼翼型的影响,仅考虑飞行姿态的影响,即假设太阳能电池组件平铺在无人机机翼上。
太阳能机翼需要考虑太阳入射光与受光平面的角度影响(即无人机的姿态角对太阳能电池组件接收太阳辐照大小的定量影响),加入太阳入射光与受光平面的夹角关系如图7-1所示。
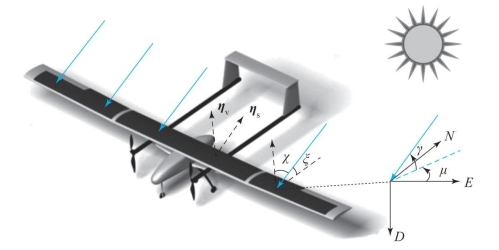
图7-1 太阳辐照和无人机飞行姿态的几何关系
太阳能电池组件表面受到的等效太阳辐射直射量S p与机翼表面受到的太阳辐射量S w的关系式如下:
![]()
式中,ξ——太阳入射光与机翼的几何夹角,可通过求取入射光与受光平面的法线的夹角χ得到,即ξ=π/2-χ。
因此,假设太阳入射光的方向向量为ηs,方向由地面指向天顶,机翼上光伏电池表面的法线向量为ηv,方向由电池指向天顶,则χ=<ηs,ηv>。太阳高度角γ为天顶角的余角φ,因此有
![]()
太阳方位角μ可通过下式求取:

式中,δ——赤纬;
κ——纬度。
由此,在地面坐标系Xg YgZg中,向量ηs表示为
![]()
在机体坐标系Xb YbZb中,ηv表示为(0,0,-1)。由机体坐标系和地面坐标系的转换关系,可得地面坐标系XgYgZg中的ηv表示为
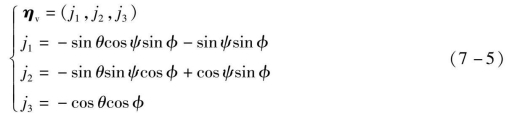
因此,太阳入射光与光伏电池表面的法线的夹角χ可通过向量夹角公式计算,即
![]()
所以,考虑无人机姿态角的太阳辐照公式为
![]()
7.1.1.2 太阳能电池模型
在均匀辐照情况下,太阳能电池单二极管模型可以精确地反映输出特性,且具有较快的动态响应速度。因此,本节采用双二极管太阳能电池模型,其等效电路如图7-2所示。
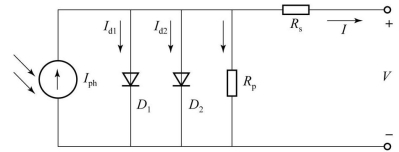
图7-2 太阳能电池双二极管模型等效电路
根据电子电路理论,可得太阳能电池双二极管模型的I-V方程如下:
![]()
式中,I——太阳能电池的输出电流;
V——太阳能电池的输出电压;
R s——太阳能电池的串联等效电阻;
R p——太阳能电池的并联等效电阻;
Id1,Id2——二极管D1和D2的反向饱和电流;
VT1,VT2——二极管D1和D2的热电压;
a1,a2——二极管D1和D2的理想因子。
Iph——太阳能电池的光电流,其计算方法如下:
![]()
式中,Iph0——辐照度为S p0时的光生电流值,本式引入了机翼上表面太阳辐照度对电池模型的影响。
为简化计算,可设定双二极管模型的反向饱和电流Id=Id1=Id2。计算式如下:
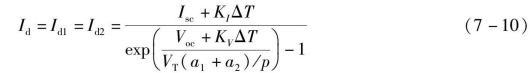
式中,KI——太阳能电池的短路电流温度系数;
K V——太阳能电池的开路电压温度系数;
Voc——太阳能电池的开路电压;
Isc——太阳能电池的短路电流;
VT——二极管D 1和D 2的热电压,VT=VT1=VT2=KT/q,K=1.608×10-23 J/K,q=1.608×10-19℃,T为环境温度;
ΔT——温度偏差,ΔT=T-Tstc,Tstc=25℃,本式将飞行器所处环境的温度引入了太阳能电池模型。
式(7-10)简化了双二极管模型的计算,使其无须迭代即可得出结果,二极管理想因子a1和a2分别代表扩散电流分量和复合电流分量。根据肖克利扩散理论,扩散电流必须是有限的。扩散电流分量为1,即a1=1。复合电流分量a2可以灵活取值,经大量试验分析得出:当a2≥1.2时,模型与实际情况最为匹配。引入中间变量p=a1+a2,可知p≥2.2,因此可将式(7-8)简化为
![]()
R s与R p之间的关系如下:
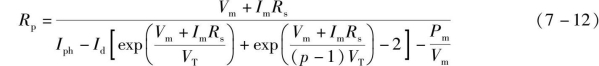
式中,Vm——太阳能电池的最大功率点电压;
Im——太阳能电池的最大功率点电流;
P m——太阳能电池的最大输出功率。
R s的任意值均有唯一的R p与之对应,可以采用迭代方式求解R s和R p。在迭代过程中,R s的初值为0,R p的初值由下式计算得到:
![]()
式中,Voc——太阳能电池的开路电压;
I sc——太阳能电池的短路电流。
7.1.1.3 氢燃料电池模型
本书燃料电池模型采用一阶等效电路模型,如图7-3所示,其中Vcell为单片燃料电池电压,R i为燃料电池内阻,R d为活化内阻和浓差内阻之和,C dl为表征电池时间响应的并联RC电路的电容。
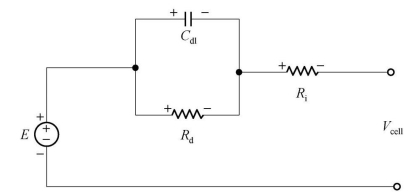
图7-3 燃料电池一阶等效电路模型
首先,根据等效电路模型,可推导燃料电池的模型如下:
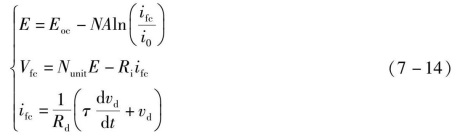
式中,E oc——开路电压;
N——每个电堆的电池片数量;
N unit——串联的电堆数量;
A——塔费尔(Tafel)斜率;
i 0——标称交换电流;
v d——电阻R d两端电压;(https://www.daowen.com)
τ——时间常数,![]()
燃料电池消耗的氢气和氧气的气压分量,分别为参与化学反应的气压分量P H2和P O2,即

式中,U H2,U O2——氢气和氧气的利用率;
P fuel,P air——燃料和空气的供应气压;
x,y——氢气在燃料中和氧气在空气中的百分比。
反应过程的氢气和氧气的利用率与燃料电池进气流率和燃料电池电流有关,即

式中,Vfuel,Vair——燃料电池燃料、空气的进气流率,L/min;
ifc——燃料电池电流,A。
考虑到化学反应动力学和物质传输过程的损耗,燃料电池实际工作时的开路电压比Nernst方程中的理论值小,这是反应物活化、内阻,以及物质扩散导致的,即
![]()
而活化压降Vact和欧姆压降Vr可由下式计算:
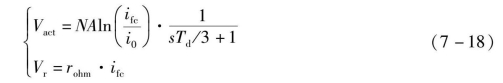
式中,Voc——燃料电池的实际开路电压;
Td——反应时间;
rohm——燃料电池内阻;
ifc——燃料电池电流。
将式(7-18)中的活化损耗通过并联电容和电阻模拟,将动态过程采用一阶传递函![]() 表示,而内阻损耗通过串联电阻表示,则燃料电池等效电路模型如图7-4所示。
表示,而内阻损耗通过串联电阻表示,则燃料电池等效电路模型如图7-4所示。
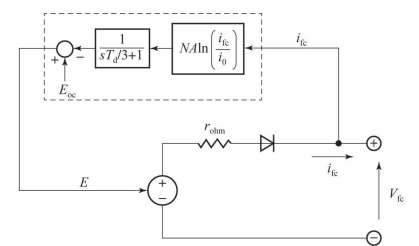
图7-4 燃料电池等效电路仿真模型
理论开路电压Eoc、交换电流i0和塔费尔斜率A取决于气体压力、温度、纯度和流速,即Eoc、i0和A的计算如下:
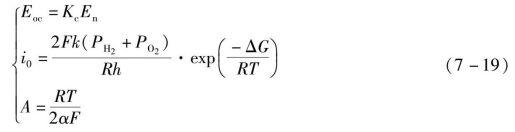
式中,R=8.3145 J/(mol·K),F=96485 A·s/mol;
E n——Nernst电压;
α——电荷转移系数;
P H2——燃料电池堆内的氢气分压;
P O2——燃料电池堆内的氧气分压;
k——玻尔兹曼常数,J/K;
h——普朗克常数,J·s;
ΔG——活化能垒,J;
T——反应温度,K;
Kc——额定工作条件下的电压常数。
储氢装置中氢气的压力状态(state of pressure,SOP)定义如下:

式中,P0——储氢装置的初始压力,bar;
Vol——储氢装置的体积,L;
VH2——氢气流率,L/min。
当SOP低于设定的最低气压时,燃料电池停止工作。
7.1.1.4 锂电池模型
锂电池模型采用改进的Shepherd曲线拟合模型,根据电流和荷电状态(SOC)来定义其电压。一般锂电池放电曲线可分为三段:第一段,电池电压随电量状态呈指数下降;第二段,近似线性下降,是锂电池的主要工作区域;第三段,电池电压急剧下降至截止电压。假定电池内阻在充电和放电周期内为定值,不考虑温度对电池模型的影响,充放电的模型参数相同,则锂电池充放电过程的电压模型为
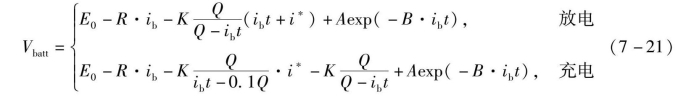
式中,E0——电压常量;
K——极化常数或极化电阻;
i*——滤波电流;
ib——电池电流;
Q——最大电池容量;
A——指数电压;
B——指数区时间常数;
R——电池内阻。
锂电池的SOC计算如下:

锂电池通常对温度比较敏感,考虑环境温度和自身温度对模型的影响,则锂电池放电和充电模型修正如下:
![]()
·放电时(i*>0)
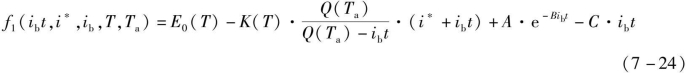
·充电时(i*<0)
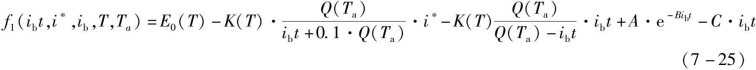
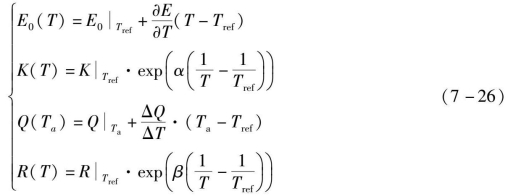
式中,Tref——标称环境温度,K;
T——电池或内部温度,K;
Ta——环境温度,K;
E/T——可逆电压温度系数,V/K;
α——极化电阻的阿伦尼乌斯速率常数;
β——内阻的阿伦尼乌斯速率常数;
ΔQ/ΔT——最大容量温度系数,Ah/K;
C——标称放电曲线斜率,V/Ah。
对于放电曲线不太明显的锂电池(如磷酸铁锂电池),该参数设置为0。
