6.2.2 基于模型预测的混合能源管理与控制
本节首先介绍模型预测控制原理;然后,以预测时域内等效氢耗最小为目标,建立氢燃料电池/锂电池混合动力系统模型预测方法,兼顾燃料电池动态特性,以氢燃料电池/锂电池混合动力系统为例,给出基于时域内等效氢耗最小的模型预测能源管理与控制流程。
6.2.2.1 模型预测控制原理
模型预测控制(model predictive control,MPC)是一种反馈控制策略,其机理是:在每一个采样时刻,根据获得的当前测量信息,在线求解一个有限时域开环优化问题,并将得到的控制序列的第一个元素作用于被控对象;在下一个采样时刻,重复上述过程,用新的测量值更新优化问题并重新求解。在线求解开环优化问题获得开环优化序列,是MPC与传统控制方法的主要区别。由于在线求解的优化问题中很容易包含各种等式约束和不等式约束,因此MPC也是处理约束问题系统控制问题的最有效方法之一。
通常,模型预测包括预测模型、滚动优化和反馈补偿等部分。在早期,有限脉冲响应模型和阶跃响应模型更受欢迎,包括动态矩阵控制和二次动态矩阵控制。有限脉冲响应模型结构对过程延迟、响应时间和增益进行了透明描述。然而,它们仅限于稳定的被控对象,通常需要较高的模型阶数。传递函数模型对过程动力学的描述更简洁,适用于稳定和不稳定的对象,但是基于传递函数模型的预测控制在处理多变量模型中通常被认为是无效的。近年来,使用状态空间设计方法的预测控制设计越来越流行,基于状态空间的模型预测控制的控制系统设计中,采用的模型是状态空间模型。状态空间模型预测未来所需的当前信息由当前状态变量表示,通过传感器测量得到。
预测控制的优化与传统意义上的最优控制的最大区别就是有限时间内的在线滚动优化。在每次采样时,优化性能指标只涉及从当前时刻开始的未来有限时域,该时域在每个采样时刻同步向前。因此,在预测控制中优化的过程是反复在线实时进行的而不是离线进行的。
在控制过程中,受实际工作过程中的各种干扰因素影响,预测模型并不能十分准确地描述被控系统的性能,导致模型预测失真,因此需要反馈并不断校正预测模型。为防止环境干扰等因素导致控制偏离,预测控制不会执行当前时域内求得的所有控制量,而只执行序列中第一个控制量;在下一时刻,将测量的实际输出与预测输出进行比较,校正预测模型,然后求解下一时刻的优化函数。
对于非线性模型预测控制来说,假设当前时刻为k,则当前预测时域内的优化目标为
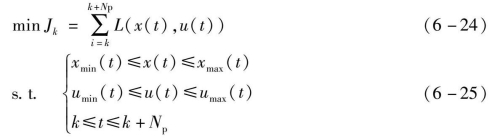
式中,Jk——预测时域内的代价函数;
Np——预测时域;
x(t)——t时刻的状态量;
u(t)——t时刻的控制量。
当前时刻的优化问题限定在预测时域k~k+Np内,对预测时域外不予考虑。
6.2.2.2 等效氢耗最小模型预测能源管理与控制策略
接下来,针对燃料电池/锂电池混合动力系统,给出基于时域内等效氢耗最小的模型预测混合能源管理策略以及流程。
1.模型预测控制系统设计
模型预测控制系统的结构如图6-12所示,使用模型预测控制来管理混合能源系统的能量分配,以实现燃料消耗最小化、燃料电池保护和锂电池SOC的维护。
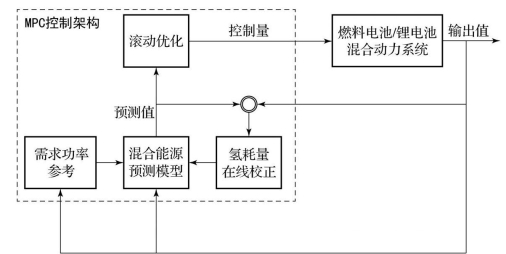
图6-12 模型预测控制系统的结构
混合能源预测模型首先根据需求功率参考轨迹、当前时刻的状态量,利用混合能源预测模型求解使目标函数最小的控制序列;然后,根据滚动优化原则,选取控制序列的第一个值作为当前时刻的控制量,控制执行机构(即DC/DC转换器)分配燃料电池与锂电池的输出功率;最后,根据测得的需求功率更新需求功率参考值,用实际测得的燃料电池瞬时氢气消耗与预测模型预测的氢气消耗进行比较,求得燃料电池预测氢气消耗的补偿,在线校正燃料电池氢气消耗预测模型。
以当前时域内等效氢耗最小为控制目标,氢燃料电池功率和锂电池功率为控制变量,构建模型预测优化模型如下:
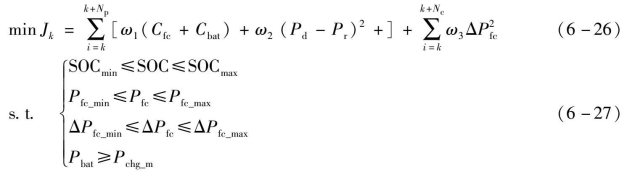
式中,Pd——需求功率;
Pr——参考功率;
ΔPfc——燃料电池功率的变化量;
ΔPfc max,ΔPfc min——燃料电池变化量的最大值与最小值;
Pchg_m——锂电池的最大充电功率;
ωi(i=1,2,3)——各项的权重系数;
Np——预测时域的大小;
Nc——控制时域的大小。
由于燃料电池功率特性较软,燃料电池功率突变量较大会对燃料电池造成伤害,因此,对燃料电池功率变化量进行约束。
2.预测模型建立
需求功率是能源管理装置的一个重要参数,影响能源优化,因此,需求功率P d ref被用作模型预测控制器的参考参数。本节以氢燃料电池/锂电池混合能源无人机为例,其中氢燃料电池为EOS600、锂电池为5300 mAh的6 S电池。
新能源飞行器在飞行中多以巡航平飞和定速爬升为主,平飞和定速爬升时功率较为稳定,所以预测功率为当前时刻的需求功率,即
![]()
式中,P d mes——当前时刻需求功率的测量值。
图6-13所示为锂电池的SOC与开路电压的关系。开路电压Uocv与为SOC的函数可记为(https://www.daowen.com)
![]()
式中,ai(i=0,1,2)由实验曲线根据最小二乘法拟合得到。
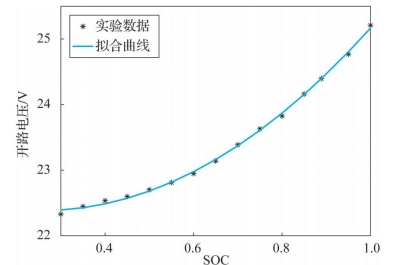
图6-13 锂电池SOC与开路电压的关系
模型预测策略的参数如表6-4所示。
表6-4 模型预测策略的参数
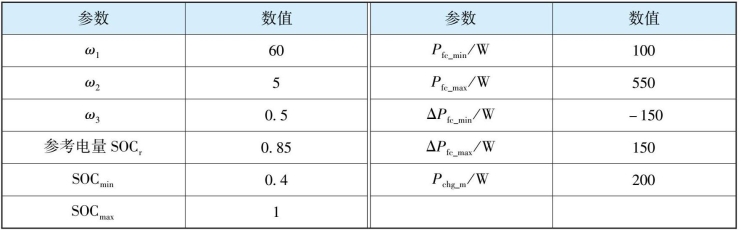
3.目标函数求解
选择二次规划方法对模型预测控制优化目标函数求解,因此需要构建方程如下:
![]()
![]()
式中,x——n维向量,n为状态变量个数;
Q——n×n矩阵;
C——n维向量;
A——m×n矩阵;
b——m维向量;
m——约束个数。
为构建式(6-30),首先将锂电池等效氢耗预测模型线性化。锂电池等效氢耗与锂电池功率、SOC的关系如图6-14所示。
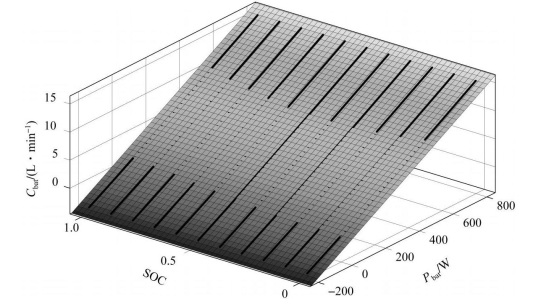
图6-14 锂电池等效氢耗拟合曲面
通过线性拟合得到锂电池等效氢耗线性模型为
![]()
然后,选择燃料电池功率和锂电池功率变化量作为控制变量,氢耗量、SOC、需求功率、燃料电池和锂电池功率为状态变量,即

混合动力预测模型状态空间模型的形式为
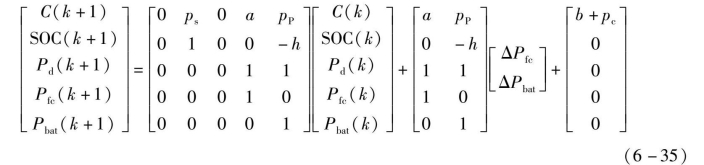
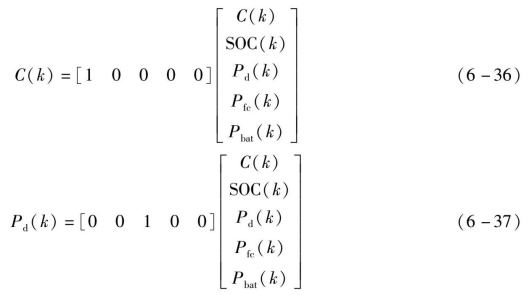
式中,![]() Δt是采样步长,Ubat和Q bat是锂电池的电压和容量。
Δt是采样步长,Ubat和Q bat是锂电池的电压和容量。
因为最后一项为常数,即不影响极值位置,故舍去,即
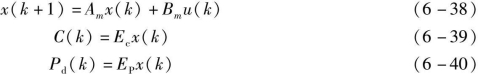
在预测时域Np内,状态变量的预测序列记为
![]()
在控制时域Nc内,控制变量的控制序列为
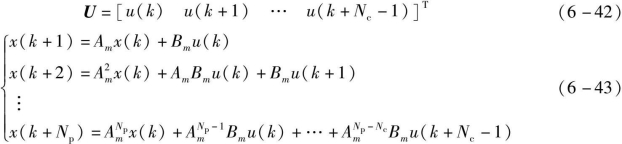
记为
![]()
假设:
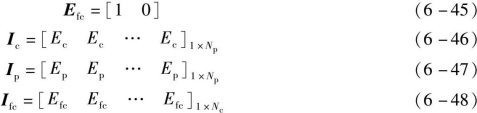
则优化目标函数为
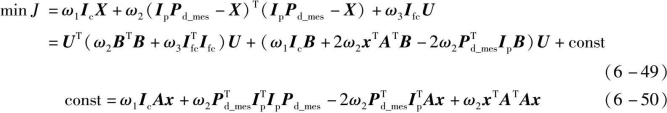
燃料电池变化量的约束为[-150,150],设
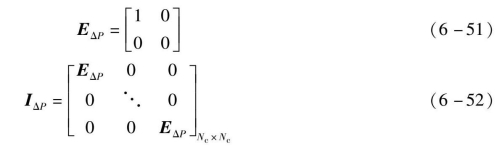
则控制量的序列约束为
![]()
式中,Umin,Umax——控制量的最小约束序列和最大约束序列。
锂电池SOC的约束为[0.4,1],燃料电池的功率约束为[100,550],锂电池的功率约束为[-200,2000],则状态量的约束序列为
![]()
式中,Xmin,Xmax——状态量的最小约束序列和最大约束序列。
