6.1.2 模糊控制能源管理策略
模糊控制是模糊数学与控制理论相结合的产物,其主要特点是:
(1)不依赖被控对象的精确数学模型,只需要根据经验知识和操作数据确定控制规则。
(2)用语言变量表示控制行为,且不同于传统数学变量,其采用语言变量的模糊性描述控制规则,从而将专家知识融入控制系统设计。
(3)以不精确推理模拟人的思维过程,介入人的经验,处理复杂的(甚至病态的)系统控制问题。
(4)鲁棒性强,对过程参数变化不敏感,适合解决传统控制方法难以处理的非线性、时变以及大滞后问题。
模糊控制能源管理策略是一种基于专家知识的人工智能控制策略。其主要优点是突破了状态机策略有限的确定性规则,能够解决混合能源系统状态不确定性特征问题,计算成本低,对计算能力要求不高,便于在线应用;其主要缺点是对专家知识较为依赖,需要开发者反复调试,无法保证控制效果的最优性,很难完全挖掘混合能源高效利用的潜力,且在不同拓扑结构间的移植性差。
6.1.2.1 模糊控制原理
图6-4所示为模糊控制的原理框图,与传统控制系统不同的是,控制器部分采用模糊控制方法。首先,参考控制信号r(t)与传感器的反馈信号v(t)进行比较,产生误差信号e(t);其次,通过模糊控制器处理,产生控制量u(t)并传递给执行机构,通过执行机构作用到被控对象上,产生输出信号y(t),这些信号在模糊控制器处理前与处理后都是清晰明确的值。模糊控制器首先将这些明确值模糊化成模糊变量;其次,经过模糊控制规则处理,得到模糊决策结果;最后,通过解模糊处理,得到清晰明确的控制输出量。
模糊控制系统的控制效果会受到模糊控制器所采用的结构、模糊控制规则和模糊推理决策方法等因素的影响。图6-5所示为模糊控制器的基本结构,其一般包含模糊化接口、模糊推理机、知识库和解模糊化接口四部分。其中,知识库中包含根据专家经验知识制定的模糊控制规则,这是模糊控制器的核心部分,是控制策略和控制经验的具体实现;其他部分主要是提供输入输出等辅助作用。
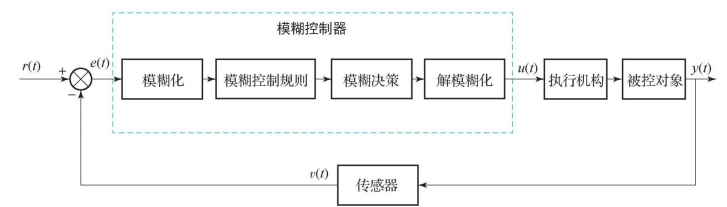
图6-4 模糊控制原理框图
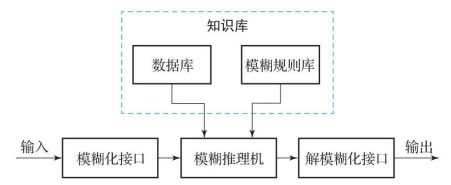
图6-5 模糊控制器基本结构
1.模糊化接口
由于模糊控制器只能处理模糊变量,因此需要采用模糊化接口对输入的明确数值进行模糊化。将模糊控制器输入量的确定值转换为相应的模糊语言变量值,是把输入的清晰量映射成模糊子集及其隶属度函数的过程,主要包括两方面:输入变量的模糊化;模糊子集隶属度函数的选取。
1)输入变量的模糊化
输入变量的取值范围有所不同。为了便于计算处理,首先将不同变化范围的精确输入量转换为所规定论域范围内的离散值。例如,对于输入信号X=[e e·],假设覆盖e的模糊论域为E={-1,0,1},对应模糊子集为“B(大)”“M(中)”“S(小)”;覆盖e·的模糊论域为[-3,-2,-1,0,1,2,3],对应模糊子集为“NB(负大)”“NM(负中)”“NS(负小)”“0(零)”“PS(正小)”“PN(正中)”“PB(正大)”。
2)模糊子集隶属度函数的选取
模糊控制中将清晰变量模糊化为模糊变量的数学体现就在于隶属度函数,它把模糊度量转换为标准的[0,1]区间,所选取的模糊子集由隶属度函数μ(x)来描述。对于连续论域的隶属度函数,一般选取三角形、梯形或高斯分布型。例如,x∈[-3,3]所对应的模糊子集为NB、NM、NS、0、PS、PM、PB,采用高斯分布函数为
![]()
式中,c——分布的平均值;
σ——标准差,取大于零的实数。σ越大,μ(x)曲线就越宽,分辨率就越低,控制特性比较平缓;σ越小,μ(x)曲线就越窄,分辨率就越高,控制灵敏度也越高。
取σ=0.36,各模糊子集的隶属度可表示为
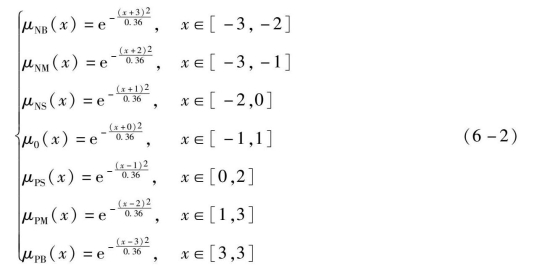
2.知识库
知识库包含数据库和模糊规则库。其中,数据库存放系统各种输入/输出变量对应的隶属度函数、规范化因子和模糊算法等,为求解模糊推理过程提供必要的数据;模糊规则库是模糊控制的核心,通过符合模糊逻辑的条件语句形式表达状态变量与控制变量之间的模糊逻辑关系。
模糊规则库由一系列模糊规则构成,设A、B和C是模糊关系或模糊命题,模糊规则的结构形式如下:
![]()
可见,模糊规则分为前提部分(IF…)和结论部分(THEN…),前提部分描述原因,结论部分描述与控制行为相关的结果。这种形式的模糊规则能够实现输入和输出的非线性映射,因此能建立通用静态非线性控制函数。
模糊命题是模糊控制器的基本单元,设x和y是语言变量,其论域分别为X和Y,其可取的语言值集合为T和F,那么以下结构:

表示模糊命题A和B。式(6-3)所示的结构表示A和B的模糊关系为AND,是经典的“与”算子。
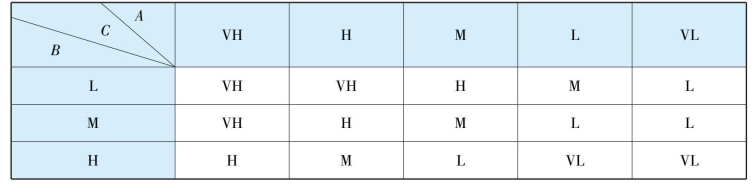
多条模糊规则构成模糊规则库,可以使用二维的模糊状态表来描述模糊控制规则库,如表6-1所示。
表6-1 模糊规则状态表
3.模糊推理机
模糊推理机是根据模糊逻辑法则把模糊规则库中的模糊规则转换成某种映射,而这种映射用于解释每条规则的意义。评价模糊规则前提部分对结论部分产生的影响称为模糊蕴涵。每条规则都可以结合模糊蕴涵关系合成推理规则,在控制应用中有两种模糊蕴涵关系最常用:乘积蕴涵(Larsen方法)、取小蕴涵(Mamdani方法)。
合成的模糊推理规则为
![]()
式中,R——模糊蕴涵关系。
两种模糊蕴涵的推理方法如下:
 (https://www.daowen.com)
(https://www.daowen.com)
式中,μRAB→RC——式(6-6)规则所采用的模糊蕴涵的隶属度;
μRAB——A与B运算后的隶属度;
μRC——命题C的隶属度。
表6-1中的模糊蕴涵关系为R i(i=1,2,…,15),则合成的模糊推理规则为
![]()
可见,模糊推理需要包含3个计算过程——与运算、合成运算、和蕴涵运算,才能构成模糊推理机的完整过程。
4.解模糊方法
模糊控制器中经过模糊推理过程得到的输出量是模糊量,不能将其直接作用于执行器实现系统控制,必须将其转换成控制执行器所需的精确量(又称清晰值)。从输出模糊集合提取精确输出值的过程称为解模糊。解模糊通常采用如下几种方法:
1)最大隶属度法
最大隶属度法是在输出模糊集合中选取最大隶属度值作为控制输出值。若输出模糊集合C的隶属度函数只有一个极值,则取隶属度函数的最大值作为清晰值,即
![]()
式中,z0——清晰值;
z——模糊变量;
Z——模糊论域。
若输出模糊集合C的隶属度函数有多个极值,则取这些极值的平均值作为清晰值。
2)面积平分法
面积平分法又称中位数法。该方法取中位数作为z的清晰值,即z0等于μC(z)的中位数,以a为下边界、b为上边界、z0为分界线,则满足下式:

3)重心法
重心法又称加权平均法。对于连续的模糊变量论域连续,则可根据面积重心原理进行积分得到清晰值,即n

对于连续的模糊变量的论域离散,则取μC(z)的加权平均值作为清晰值,即

6.1.2.2 模糊控制能源管理策略设计
本节针对氢燃料电池/锂电池混合主动拓扑能源系统,给出模糊控制能源管理策略设计示例。该系统的状态变量包括锂电池电量状态SOC和需求功率P D,而控制量为燃料电池输出功率,即燃料电池经过DC/DC功率转换器后的输出功率P fc。模糊控制器的输入输出关系如图6-6所示,燃料电池无人机需求功率P D和锂电池电量状态SOC为模糊控制器的输入变量,通过分析两者变化合理决定模糊控制器输出变量P fc,而锂电池的功率则由功率平衡原则自动补偿。

图6-6 模糊控制器的输入输出关系示意图
1.状态和控制变量模糊化
将需求功率P D模糊化为5个子集,即[VH,H,M,L,VL];将锂电池电量状态SOC分为高、中、低3个模糊子集,即[H,M,L];将氢燃料电池的输出功率P fc模糊化为5个子集,即[VH,H,M,L,VL]。
2.隶属度函数设计
采用梯形隶属度函数,分别设计需求功率P D、锂电池当前电量状态SOC和燃料电池输出功率P fc在论域范围内的隶属度函数,如图6-7~图6-9所示。
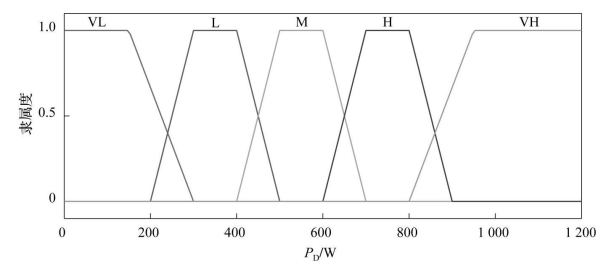
图6-7 需求功率隶属度函数
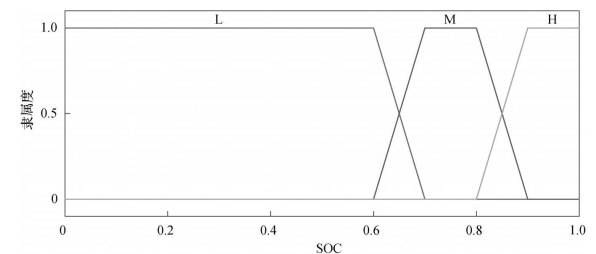
图6-8 锂电池当前电量隶属度函数
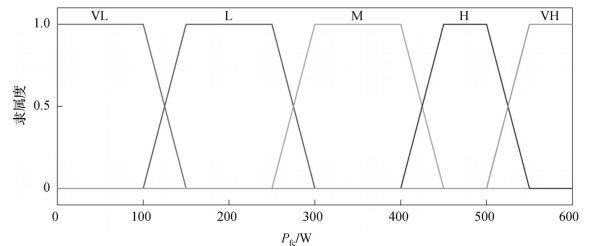
图6-9 燃料电池输出功率隶属度函数
3.模糊规则设计
模糊规则是模糊推理机的核心,对于氢燃料电池/锂电池混合动力飞行器,制定其模糊控制能源管理规则的原则如下:
(1)燃料电池为主能源。考虑到其电力特性较软的特点,应尽可能使其工作状态较为平稳,避免大波幅暂态功率输出;为了节省燃料,燃料电池应尽可能工作在高效点附近。
(2)锂电池为辅助能源,主要处理高频、大波幅、暂态需求功率,考虑到其循环使用寿命,应将充放电倍率限制在合理的范围之内。
(3)为了保证锂电池有一定电量,使飞行器具备应急机动的能力,燃料电池应能为锂电池充电,且尽可能在高效点附近为锂电池充电。
(4)锂电池电量较高时,就强化锂电池的放电能力,弱化对锂电池充电,减少燃料电池的输出。燃料电池主要用于满足剩余需求功率。
(5)锂电池电量中等时,根据需求功率情况,燃料电池起主导作用,锂电池辅助配合;需求功率较小时,燃料电池可为锂电池充电。
(6)锂电池电量较低时,燃料电池所起的主导作用进一步强化,锂电池则弱化放电,强化充电。
(7)每时每刻都要满足总线需求功率P D与燃料电池功率P fc和锂电池功率P b之间的功率平衡原则,即
![]()
根据以上原则,所设计的模糊规则如表6-2所示。
表6-2 模糊控制器模糊规则
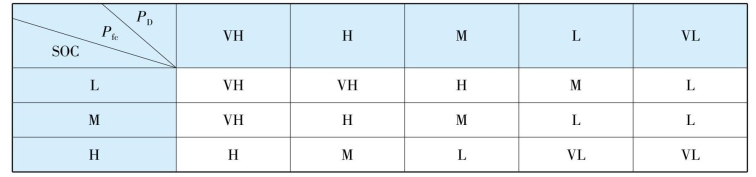
确定模糊规则后,经过模糊推理和解模糊,就可以得到控制量输出的清晰值。
