1.2 研究意义及简介

2025年09月26日

版权

1.2 研究意义及简介

经济的飞速发展推动了汽车行业的空前繁荣，车辆越来越多地介入人们的日常生活，统计数据和研究资料表明，城市用车平均时间日益增加， 81.8％的车主需要每天驾车1～2个小时，这就促使人们对车载信息服务也提出了更多更高的需求［1］。如何充分利用道路资源，将人、车、资源和谐统一起来，组合成满足不同用户不同功能需求的复杂服务，将具有重要现实意义和广阔应用前景。然而，由于VANETs中车辆节点的快速移动性，以自组形式形成的网络时而断开，时而又形成新的网络，网络拓扑变化迅速、网络稳定性和连通性较差，这些特性使得基于传统有线网络的服务组合成果和技术不能够适应于VANETs领域，服务组合面临严峻挑战。考虑到VANETs高度动态性，致力于动态网络下的服务组合研究，本书将建立一套适应于车载网络移动终端的服务组合体系框架及相关机制，具体可归纳为以下几点，如图1.1所示。

①VANETs车载终端高动态性导致网络拓扑结构实时变化，进而对服务组合建模或形式化描述设置了相当的障碍和难度。本书在深入分析目前服务组合系统方案优缺点的基础上，提出了一种面向VANETs服务组合的层次覆盖网络架构，在此基础上设计基于服务覆盖层的服务组合模型。首先，借鉴服务覆盖层SON设计思想，将VANETs这种动态分布式服务组合体系结构从逻辑上划分为物理网络层、服务实例层、服务抽象层三个层次，并通过建立功能、服务、路由之间的映射关系，采用动态叠加部署策略抽象出了第四层服务覆盖层。其次，分析用户服务组合请求与服务覆盖层上覆盖节点及覆盖链路的相互关系后，结合VANETs移动特性，构建了VANETs下的服务组合模型。

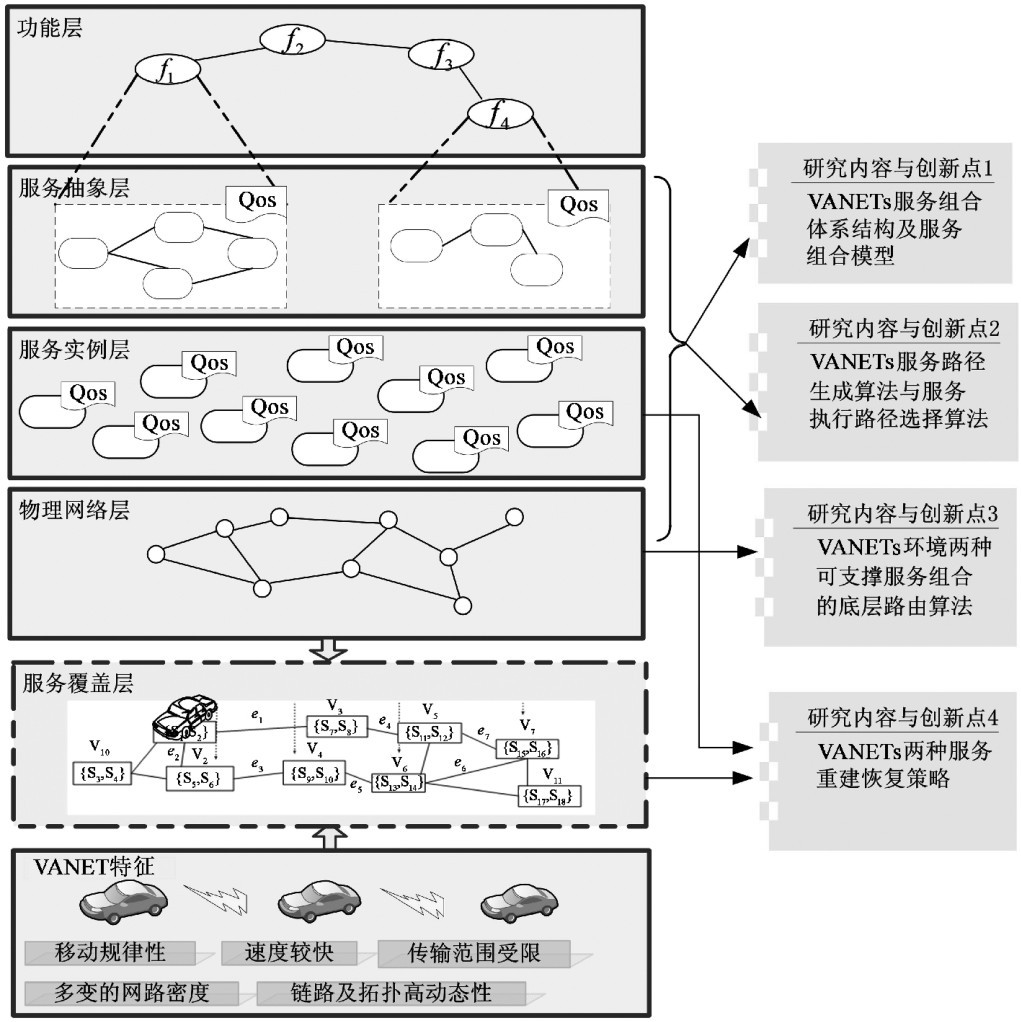
图1.1 研究内容及创新点

②在服务组合模型分析基础上，本书将模型求解问题转化为服务路径生成、服务执行路径选择及服务路径维护三个过程。首先，在传统的基于经典图论（Directed Acyclic Graph， DAG）理论的服务组合算法中改进并提出了基于服务强度及链路生存时间的服务路径生成算法。其次，为有效进行服务执行路径的选择，本书设计了驱动服务选择的服务覆盖层QoS模型，并在QoS驱动下提出2⁃level打分机制的服务执行路径选择算法（Local Optimal Service Path Selection Algorithm， LOSPSA），该算法将底层车载节点的移动特性与服务执行路径选择的相关信息紧密融合，在有效降低网络拓扑关系复杂度的同时提高了对用户服务组合需求的动态适应性。第三，为一进步确保服务组合路径的有效性及可行性，从预测链路稳定性出发，提出了主动性服务路径维护策略，设计了带有服务切换功能的服务执行路径维护算法（Velocity and Distance Based Handoff Algorithm， VDBHA）。

③目前支撑服务发现、组合机制的底层路由算法的研究并没有充分考虑与服务选择的自适应性，针对性较弱。为更好地对上层服务以及服务组合模型提供良好的网络路由策略，本书分析了服务组合发现选择进程与底层路由算法自适应的关系，从微观角度分析了服务组合与路由协议关联性。为提高服务组合的成功率、减少不必要的时延及网络开销，面向不同应用场景设计了两种路由算法：对于非实时性业务，采用基于节点运动方向的类AODV路由算法（Direction Based AODV Routing Protocol，DARP），可在保证服务路径质量的前提下大大提高服务路径的稳定性；对于实时性要求较高的场合，采用基于数据报报文点决策的路由算法（Datagram Based Node Routing Protocol， DBNP），可大大降低服务路径建立时延。

④为有效应对VANETs服务节点和链路频繁失效问题，本书提出了一种基于服务实例层的服务组合重建算法（Service Recoverybased on Service Level， SRBSL）， SRBSL是一种典型的先验式服务组合恢复策略，它在服务组合失效之前就根据对服务链路稳定性以及服务组件当前状态的分析来选择并维护备份服务副本，依托服务实例层中实时维护的服务副本替换策略完成对失效组合服务的重建。对于服务失效概率极大的VANETs环境， SRBSL服务恢复策略是一种有效地重建策略。为进一步提高组合服务重建算法的快速恢复性及可靠性，在VANETs层次覆盖服务组合模型研究基础之上，借鉴Overlay的设计思路，基于服务覆盖层SON综合提炼各层代价，建立服务路径失败对用户造成的干扰模型，从尽量减小服务失败对终端用户影响的角度出发提出了一种基于跨网络协议层设计的服务组合恢复架构和最小干扰的启发式服务恢复算法（Recovery heuristic algorithm， RHA）。