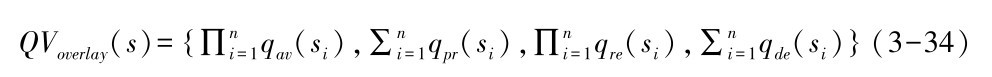3.3.1 支持服务覆盖层的QoS模型
QoS模型不仅作为服务选择的有效参考， 在诸多功能相同或者功能重叠的服务中进行服务区分， 更重要的是将非功能属性及用户的个性化服务需求从模型角度进行量化分析，从而驱动整个服务组合进程的执行［59，60，61］。针对于前面提出的VANETs服务组合模型， 笔者从物理网络层特性及服务实例层属性两方面综合提炼来设计服务覆盖层上用户感知的QoS模型。 下面就分别从这两个层次来提取QoS属性， 采用跨层设计思路对QoS模型进行建模。
（1） 物理网络层QoS属性
首先， 我们提出影响上层服务选择的几个物理网络层关键属性， 分别是网络可用性 （节点可用性）、 网络时延、 网络传输价格和网络可靠性。 下面分别就四种QoS属性展开深入研究， 给出相关定义及形式化描述。
节点可用性是QoS驱动服务选择进程中一个重要决策依据， 不仅体现节点可用和不可用状态， 还可表明在多个候选节点可用的状态下， 哪个 “更可用”［62］。同时，节点可用性也直接反映了网络可用状态， 服务路径上任一节点的失败都会导致网络层相应拓扑结构发生变化， 当前服务路由失效。 本书首次给出可用节点 （Available Node） 的定义， 在此基础上对节点的可用性状态作进一步定量分析， 给出关于节点可用性的量化评估定理。
定义3.9 （可用节点Available Node）：
节点FWi上所承载的服务组件s恰为另一节点FWj上实现某功能的候选原子服务，且FWi位于节点FWj的有效传输范围内，则节点FWi为FWj的可用节点。
定理3.1：
FWi是FWj的可用节点，则在服务执行时间t内节点FWi上承载的服务s对于节点FWj的可用性表示为qnav（s），qnav（s）＝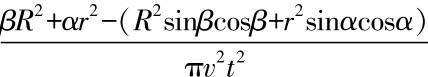
。其中，R为节点有效传输范围，v为节点FWi平均速度，r为时间t内节点FWi运动覆盖半径，d为节点FWi和节点FWj的距离，α、β分别为两节点连线与运动覆盖半径之间以及两节点连线与有效传输半径之间的夹角。
证明：FWi位于节点FWj传输范围内的概率为PINi ＝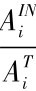
.其中，ATi为时间t内，节点FWi的运动覆盖范围；AINi 为在FWj有效传输范围内的部分。
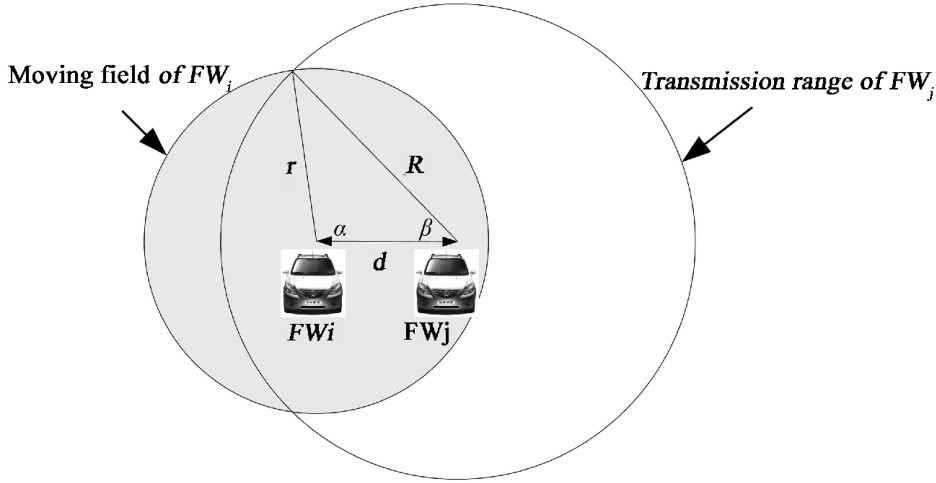
图3.5 节点 （网络） 可用性示意图
假定车载节点FWi和FWj遵循MH移动模型运动规律，两节点传输范围均为R，坐标分别为（xi，yi），（xj，yj），根据欧几里得距离公式计算两节点之间的距离d＝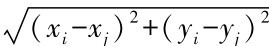
。在服务平均执行时间t内，节点FWi运动覆盖范围的半径记为r＝v×t。本方法中从统计学角度设t为服务路径中前n个服务组件的平均执行时间，即t＝∑ni＝1ti/n，则节点FWi的运动半径r可得。
依据上述分析， 如图3.5所示， 我们可以得到
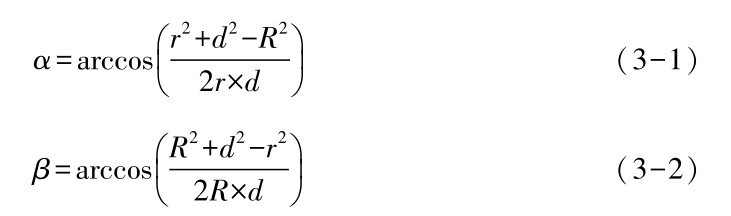
由公式（3－1）， （3－2） 及图3.5，可推出节点FWi运动场中位于节点FWj传输范围内的部分AINi
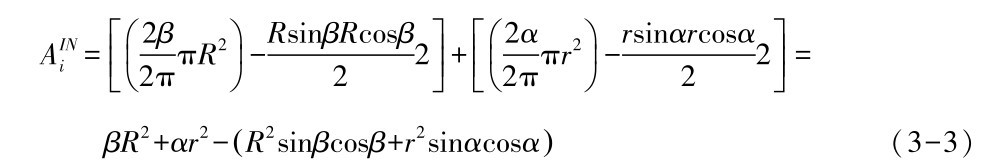
且FWi的运动覆盖范围为ATi
ATi＝πr2＝π×（v×t）2 （3－4）
由上述公式可得节点可用性，即节点FWi在服务执行时间内位于节点FWj传输范围内的概率PINi ＝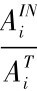
表达为：
则节点FWi（承载服务s） 对于节点FWj可用性为：
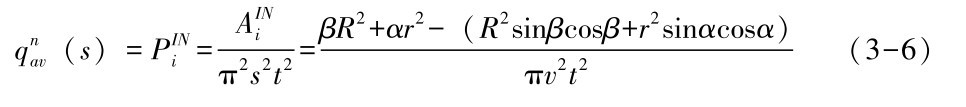
至此，节点可用性证明完毕， 定理3.1成立。 因而， 可以通过公式 （3－6） 实时评估节点可用性， 从模型角度定量分析物理网络层中节点的可用状态。
接下来我们继续讨论影响上层服务选择的另外一个关键因素，时延［63，64］。时延也是QoS性能参数中一个关键的指标， 它直接决定着用户的满意程度。若无法满足用户对于服务响应时间上的要求， 则其他性能指标的优劣也就毫无意义。基于随机过程、排队论等相关内容的研究与分析，文献［65，66］论证了在具有n个节点的移动网络中， 平均每个数据包的网络时延D（n） 取决于每一次报文转发时的节点速度v（n），则D（n） 可表达为［65］：
基于上述分析，我们提出VANETs物理网络层网络时延qnde（s）的定义。
定义3.10 （网络时延）：
网络传输过程中，报文所经历的每一次转发时间之和叫做网络时延qnde （s）， 记作：
qnde（s）＝Ο(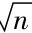
/v（n）) （3－8）
依据公式 （3－8），可以量化评估物理网络层中路由链路的平均时延， 从而为上层服务组件实例化提供有效决策依据。
另外一个影响上层服务选择的关键属性是网络传输价格， 尤其是在带宽资源稀缺时， 网络传输代价要作为一个重要的指标衡量服务路径的性能优劣。
定义3.11 （网络传输价格）：
网络中相互通信的节点Ni和Nj在某时刻t的传输单价为Pnij（t），其中m为两节点间的数据包数目。 于是通信链路在时刻t的传输价格为：
Pntc（t）＝∑m Plij（t） （3－9）
现在介绍本章构建的物理网络层QoS模型中最后一个性能指标， 网络可靠性。 与有线固定网络相比， 服务组合进程中无线网络的可靠性显得更加重要。本方法中采用无线链路的丢包率η来衡量网络可靠性qnre（s）。
通常情况下丢包率η由两个原因造成： 一方面， 由服务队列溢出造成数据包丢弃的概率为Pd；另一方面，由无线信道或网络设备等其他原因造成数据包发生错误的概率为Pe，则数据报文被节点成功接收的概率为（1－Pd）（1－Pe），丢包率为η＝1－（1－Pd）（1－Pe），因此我们给出如下定义。
定义3.12 （网络可靠性）：
服务提供节点上服务组件s的网络可靠性，
qnre（s）＝1－η＝（1－Pd）（1－Pe） （3－10）
定义3.13（服务路径Ps网络可靠性）：
服务路径Ps的网络可靠性记为qnre（Ps），
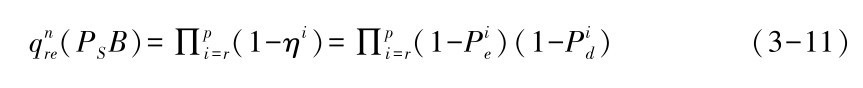
其中Pie表示节点i上数据包由于无线信道或网络设备导致报文出错概率， Pid表示节点i队列溢出导致的报文丢弃概率。
目前，求解Pie和Pid的方法有很多，根据无线信道特征及媒体接入控制的不同， 研究者习惯采用不同的方式进行求解。 本书采取Markov⁃Chain理论来对时隙划分的无线信道进行Pe和Pd的求解［67，68］。首先我们讨论Pe的求解。 为简化起见， 假定报文出错是由于叠加高斯白噪声， 报文出错率 （Packet Error Rate，PER） 可表达为［67］：
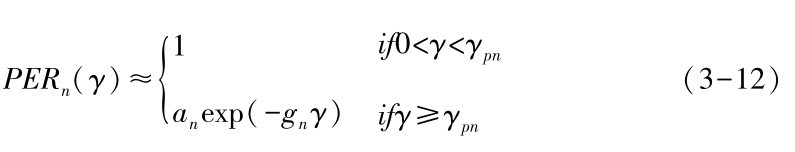
其中，n传输模型的索引数，γ为接收到的信噪比，an，gn，γpn可通过查表3.1获得［67，69］。
表3.1 基于不同调制标准的传输模型
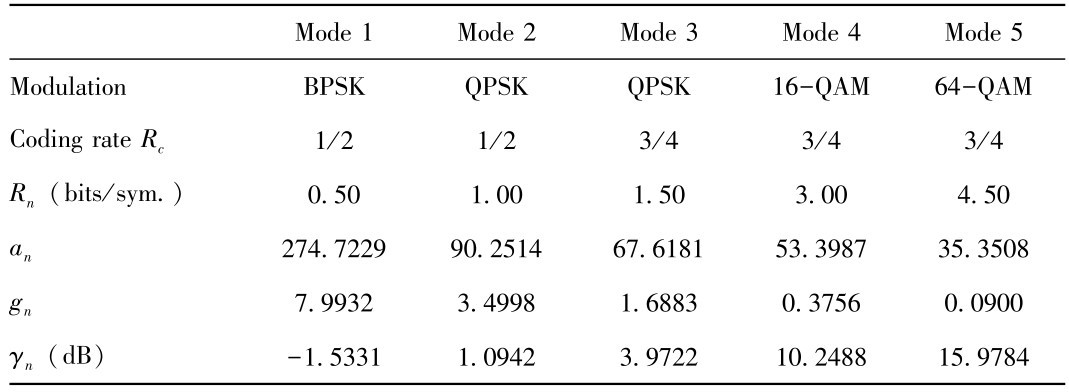
值得注意的是， 物理层每帧接收到信噪比γ是一个随机变量， 其概率密度函数如公式（3－13）所示，其中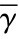
：＝Eγ{}，Γ（m）：＝
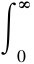tm－1exp（－t）dt，m为Nakagami衰落因子［69，70］。
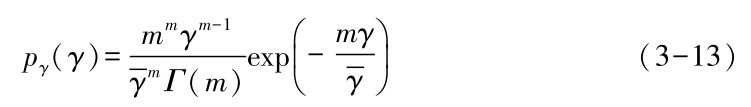
令N表示基于不同调制标准的传输模型个数， 如表3.1所示N＝5， 我们假设信道有恒定传输功率，且信噪比SNR可被划分成N＋1段互不重叠的连续范围间隔，则边界点可表示为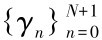
， 传输模型n的信噪比取值为γn，γn＋1[ )，根据上述分析，模型n被选取的概率为
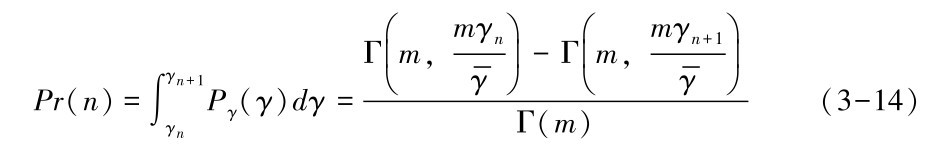
其中，Γ（m，x）：＝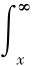
tm－1exp（－t）dt。由公式（3－13） 及公式（3－14）可推导传输模型n中报文出错率的平均值PERn
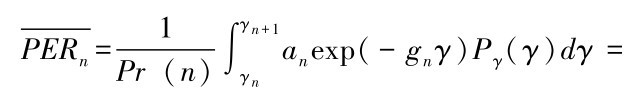
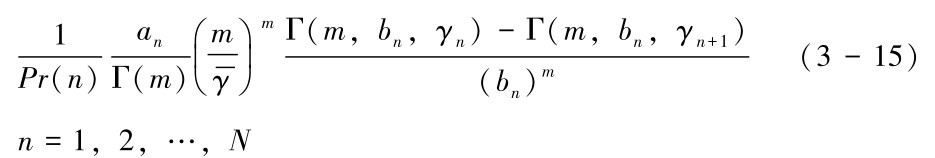
其中，bn：＝m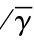
＋gn，依据公式（3－15），利用数理统计的相关知识可以推导出由于无线信道原因而造成平均数据包出错率的一般公式［68，71，72］：
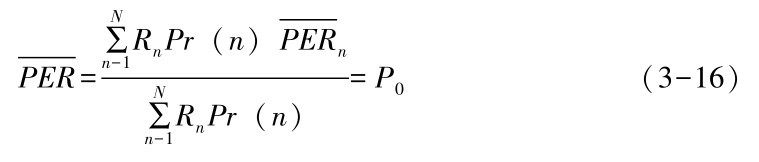
寻找到合适的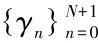
门限值，PER便等于我们预先设定的数据包出错率P0，至此，得到Pie，数据包由于无线信道或网络设备导致报文出错概率可知。
下面我们推导由于服务队列溢出造成数据包丢弃的概率为Pd，图3.6所示为节点接收端口消息队列示意图。
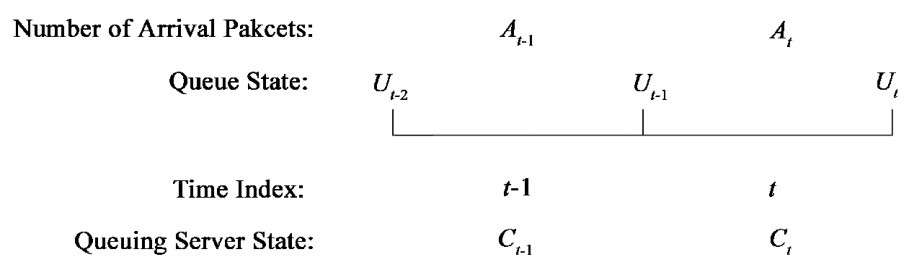
图3.6 端口队列示意图
如图3.6所示，令Ut表示在时隙t内的当前队列状态，即排队等待的报文数目，我们将Ut表示为Ut∈μ： ＝ 0，1，…，K{ }，假定发射机在时隙t一开始时先将要发送的Ct个报文移出队列，此时队列中数据包的个数为：
Lt＝max0，{ Ut－1－Ct} （3－17）
则队列中空闲隙为
Ft＝K－Lt＝K－max{0，Ut－1－Ct} （3－18）
接下来我们考虑接收数据包时的情形，如果数据包到达个数At≤Ft，则队列状态为Ut＝Lt＋At；如果数据包到达个数At＞Ft，则只有Ft个数据包可以被接收，其他At－Ft个数据包将被丢弃，相应的队列状态为Ut＝K。综上所述，在时间单元t内，队列的状态Ut可表达为：
Ut＝min{K，max{0，Ut－1－Ct }＋At} （3－19）
令Dt在时段t内丢弃的报文数据， 则根据公式 （18） 和公式 （19）可得，
Dt＝max{0，At－Ft}＝max{0，At－K＋max{0，Ut－1－Ct}} （3－20）
其中，令A：＝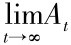
，可得：P（A＝a）＝P（At＝a） 且E｛A｝ ＝E｛At｝＝λTf，因此Dt的静态分布可以表达为：
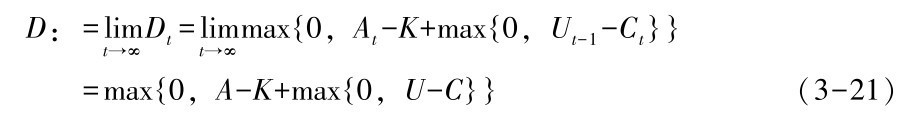
由上式可得全局范围内， 每个时间单元的丢包率为
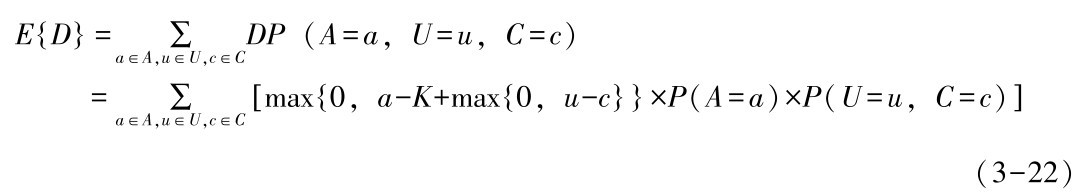
经过推导，可以得到因队列溢出造成数据包丢弃的概率Pd为
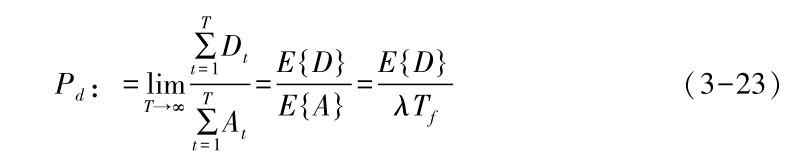
其中，λ为数据包到达速率，Tf为帧长。至此，Pe及Pd求解完毕，服务路径Ps的网络可靠性由公式（3－11） 计算得到。
鉴于对网络可用性、 网络可靠性、 网络时延及网络传输价格的推导和分析， 本书建立服务覆盖层上影响服务选择的物理网络层四维QoS模型， 记作QVnet（s）＝（qnav（s），qnpr（s），qnre（s），qnde（s））
（2） 支持服务覆盖层的用户体验QoS模型
我们将服务实例层中组合服务的QoS服务质量与上文研究的物理网络层QoS属性相结合， 从用户体验角度提出一种支持服务覆盖层的跨网络协议层QoS模型来驱动VANETs下服务选择及服务路径建立。 同样， 基于用户感知的QoS模型涉及的服务质量参数包括： 服务可用性、 服务价格、 服务可靠性和服务时延四个指标。 下面分别给出定义及模型描述。
定义3.14 （服务可用性）：
服务s可被用户成功访问的概率quav（s）。表达为quav＝qnav·qsav，其中qnav为网络可靠性，qsav为服务本身正常运行的概率。
事实上一个服务为用户可用需要同时满足以下两个条件： C1网络链路状况良好， 满足一定的网络可靠性； C2服务s本身运行正常。 因此， 从用户感知角度来说， 可将服务的可用性建模为：
quav＝qnav·qsav （3－24）
其中，qnav可由公式（3－6） 求得，qsav可表达为在监测区间δ内服务可用时间Ta（s） 所占的比率
因此， 基于服务覆盖层用户感知的QoS模型中服务可用性可得。
定义3.15 （服务价格）：
包括服务代价 （service cost） 和传输代价 （transmission cost）。 服务s的价格qupr（s）＝qusc（s）＋qntc（s），其中qusc（s）表示服务代价，qntc（s） 表示网络层传输代价。
本方法服务价格qusc（s）由服务提供者写入服务相关描述中；而qntc（s）由公式 （9） 计算。
定义3.16 （服务可靠性）：
用户的服务请求在最大期望时间内被正确处理的概率。
用户感知的服务可靠性通常由两部分决定， 一方面是执行服务s的软、 硬件配置； 另一方面是服务请求与服务提供节点之间的网络链路状况即网络可靠性。我们分别用qcre（s）和qnre（s）表示上述的两部分的概率，因此用户感知的服务可靠性可表达为
qure（s）＝qcre（s）·qnre（s） （3－26）
qcre（s）为服务s成功执行与总调度执行的比率，可由历史数据计算得到，记为
qcre（s）＝Nf（s）/T（s） （3－27）
其中，Nf（s） 为在最大期望时间内服务s被成功执行的次数；T（s） 为对于服务s总的请求次数，由公式（3－11）、（3－26） 和（3－27） 可得用户感知服务可靠性为：
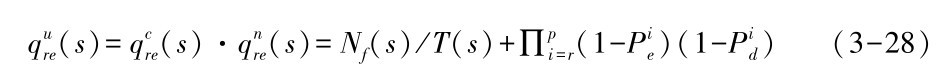
定义3.17 （服务延迟）：
用户开始请求服务和收到响应之间的时间区间，记为qude（s），qude（s）＝Tlocal（s）＋qnde（s）。
用户感知的服务延迟由两部分时间组成， 一部分是本地处理时间即服务执行时间Tlocal（s），另一部分是网络时延qnde（s）。在移动终端计算能力强大的情况下，本地进程处理时间可以被忽略，即默认Tlocal（s）＝0；但对于一些计算密集型的服务，如视频编、解码服务，Tlocal（s） 作为影响服务质量的关键因素不容忽视， 由服务提供者在服务描述中给出或通过一些询问机制发布给用户，而qnde（s）由公式（7）求得。
基于上述定义及分析， 我们提出了一种可扩展的基于用户感知的适应于服务覆盖层的四维QoS模型
QV（s）＝（quav（s），qupr（s），qure（s），qude（s）） （3－29）
以上情况我们假定用户体验对象为原子服务。 实际服务组合中， 我们要进行最优决策的是多条可满足用户功能需求但非功能属性各异的服务执行路径， 因此， 本章给出驱动服务选择及服务执行路径建立的QoS模型， 记为QV（s）＝（qav（Ps，t），qpr（Ps，t），qre（Ps，t），qde（Ps，t））
其中，服务路径Ps在时刻t的可用性qav（Ps，t） 等于该路径上所有服务组件在服务覆盖层上可用性之积
服务路径Ps在时刻t的价格qpr（Ps，t） 等于该路径上所有服务组件在服务覆盖层上价格之和
服务路径Ps在时刻t的可靠性qre（Ps，t） 等于该路径上所有服务组件在服务覆盖层上可靠性之积
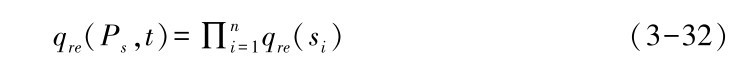
服务路径Ps在时刻t的时延qde（Ps，t） 等于该路径上所有服务组件在服务覆盖层上时间延迟之和
基于上述分析， 提出了支持服务覆盖层驱动服务路径生成及执行路径选择的QoS模型
