4.2.2 路由协议模型与分析
目前针对VANETs网络路由协议的验证仅仅停留在仿真分析阶段， 并没有从模型化角度对其进行定性分析与定量描述。 于此， 本书针对VANETs路由协议的关键性能进行模型化分析， 为路由协议的设计提供了一种相对准确的定性与定量分析相结合的决策依据。 研究从经典的路由协议AODV入手，在模型分析基础上进行相应路由算法的改进， 设计可靠性及稳定性相对更高的VANETs网络路由协议， 从而为上层服务发现与选择提供更有效的支撑。
前提假设： VANETs中所有节点均匀分布在MH移动模型中。 假定在网络中随机选择客户节点作为源节点， 源点又随机选取VANETs中其他节点作为目的节点。 物理层和MAC层采用802.11标准， 符合实际VANETs系统的条件且具备理想通信能力， 无线传播模型选取贴近实际道路环境的Shadowing模型。假定VANETs移动场景中节点总数为N，道路总长度为Lr，而其中每个节点Ni的单跳有效通信范围Lt内均存在mi个同向邻居节点，ni个反向邻居节点， 节点的平均移动速度为V，β为单位时间内同向节点的链路断链概率， 源与目的节点的平均距离为Lh。
定理4.1：
采用AODV路由协议的VANETs中，对应于服务需求时间Tl内，每一对车辆通信节点发生的平均断链次数可表达为
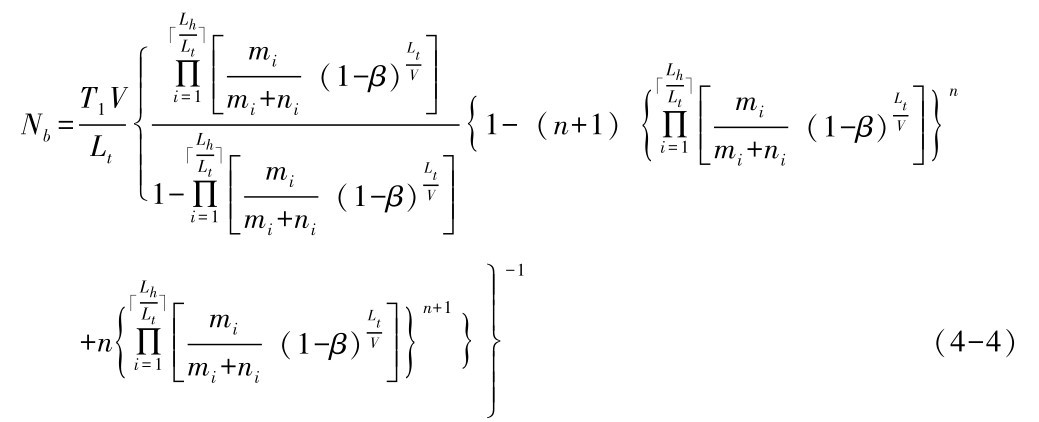
证明： 由前提假设可知， 同一条道路上反向运动两节点间的链路生存时间为T0＝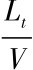
，而节点Ni在链路生存期T0内选择同方向节点作为下一跳的概率为Pm＝
。
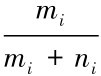因此可以得出：T0时间内该同向节点链路稳定的概率为Ps＝（1－β）T0＝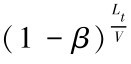
，其中，Lh为源节点和目的节点的距离，Lt为一跳的通信范围，
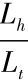表示其所定义的路由跳数（向上取整），因此在T0时间内，单条路由维持链路稳定的概率为：
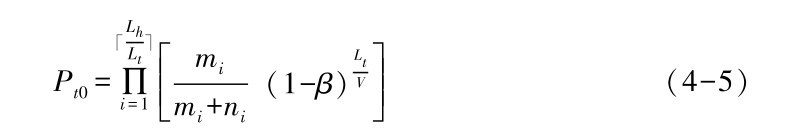
也就是说，在每一个T0时间内，路由维持链路的概率是Pt0，发生断链的概率是1－Pt0，那么单条路由的平均路由维持链路时间（数学期望）Tsta可按照离散随机变量的数学期望来求，Ex()＝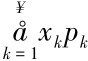
，其中xk表示链路维持时间分别是T0，2T0，3T0，…n T0这些时刻，pk表示链路维持时间分别为T0，2T0， 3T0，…n T0时，这些事件所对应的概率：
表4. 6 链路维持时间概率值
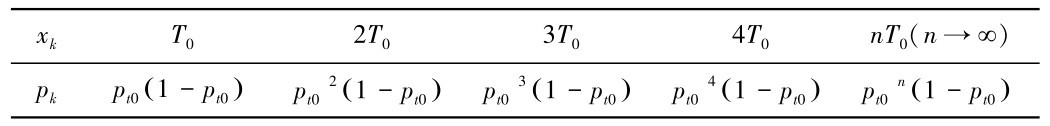
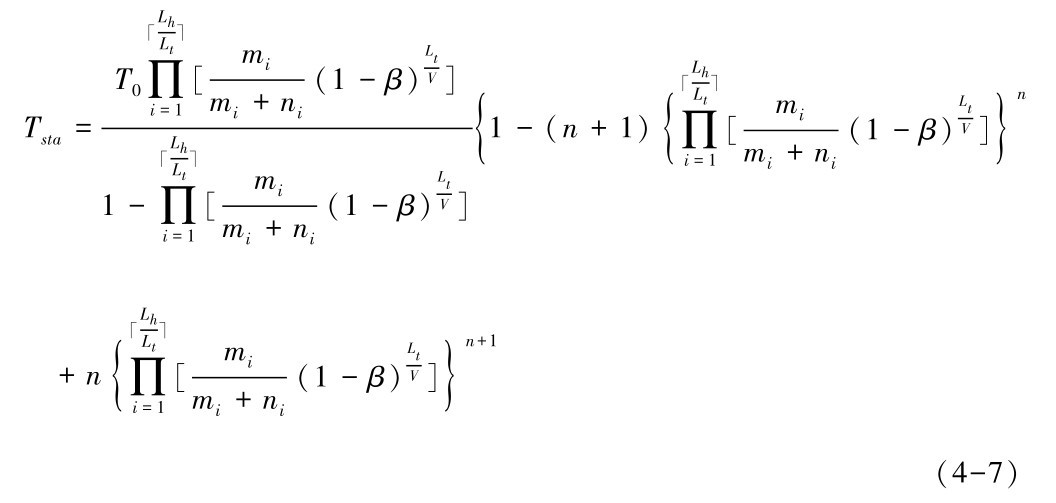
AODV中， 路由在每一次发生断链后会重新启动路由发现的过程， 因而，每一对车辆通信节点在服务需求时间Tl内发生的平均断链次数Nb可表达为
Nb＝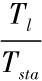
，将Tsta代入，得到
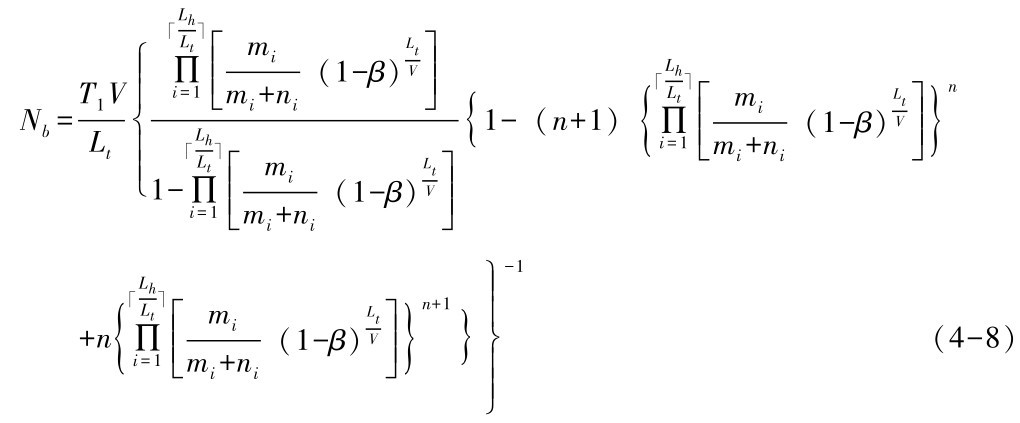
因此， 根据以上分析， 定理4.1证明完毕。
定理4.2：
在服务需求时间Tl内，AODV中每一条链路发送或转发的控制报文RREQ平均数量可表达为
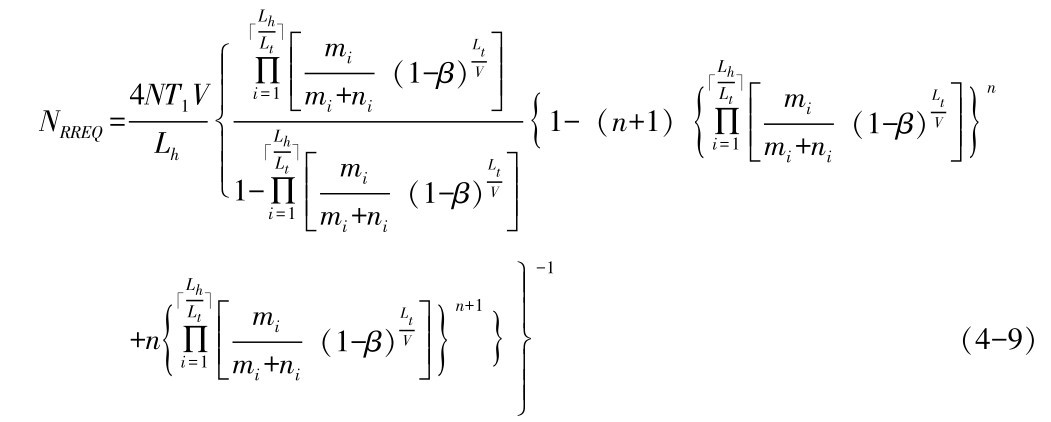
证明： 由前提假设可知， VANETs中每个车辆节点其平均邻居节点个数为Nnb＝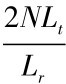
，而实际情况下控制报文RREQ的最大生存周期近似于两倍的通信节点间的路由跳数LhLt，因此每一条通信链路的控制报文平均转发次数可以表达为
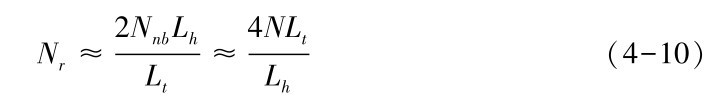
基于上述分析，我们可以得到，在服务需求时间Tl之内，经由每条链路发送或转发的控制报文平均数量应为NRREQ＝NrNb，将Nr和Nb分别代入，可得
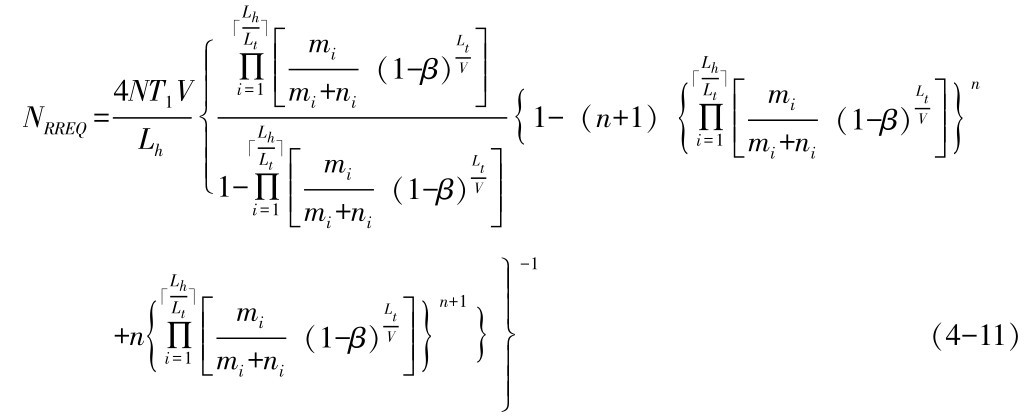
至此， 定理4.2证明完毕。