5.2.3 最小干扰服务恢复启发式算法RHA

5.2.3 最小干扰服务恢复启发式算法RHA

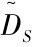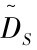分析上节提出的服务恢复策略的特征， 我们提出基于最小干扰的服务恢复启发式算法 （Recovery heuristic algorithm， RHA）。 在探测到支撑服务组合路径的底层物理链路断裂后发起服务重建， 恢复进程分为两步： 首先进行网络层的重建， 若仍无法完成组合服务的修复， 再尝试服务层的重建。 基于上述分析， 本书将基于服务覆盖层的服务组合恢复算法RHA分解为两个子问题：一是网络层重建 （Network－Level RHA， NLRHA）； 二是服务层重建（Service－Level RHA，SLRHA）。其中，服务层恢复启发式算法SLRHA是本书深入讨论的问题。 SLRHA服务恢复算法目标是通过选择最优服务路由， 使得相应服务层用户感知干扰强度最小，可以定义为

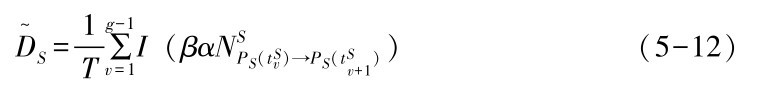
因此， 服务层上最初服务组合路径可通过求解下式得到

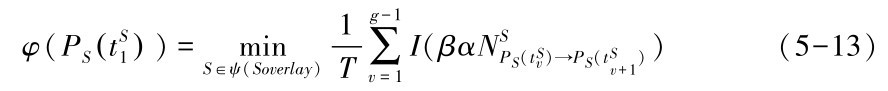
假定在时刻tsw服务路径为PSt Sw( )，则从服务路径PSt Sw( )过渡到PSt Sw＋1( )的服务恢复策略可通过求解下述公式得到

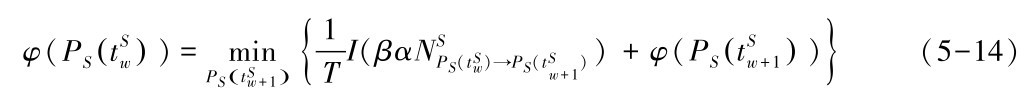
网络层的重建NLRHA相对简单， 它是在一条服务链路的生存期内从网络层面最小化干扰强度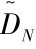所得到的路由恢复策略， 即

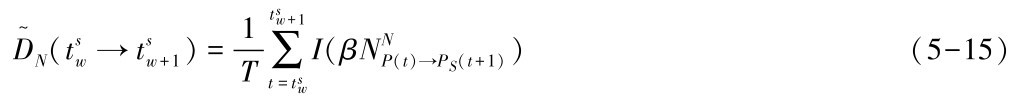
本书将重点探讨服务层的恢复算法SLRHA， 而对于网络层的重建则借鉴并依托路由协议本身的恢复机制来实现。

基于用户感知的服务层恢复算法SLRHA需要预测并考虑下一时刻网络的拓扑结构信息来确定当前的服务恢复策略，也就是说在t Sw＋1时刻的服务恢复策略要依据这个时刻之后的拓扑结构信息来计算切换到下一服务路径的最小干扰强度φ（PSt Sw＋1( )）。求解该问题存在一定的难度，首先VANETs节点快速移动导致网络拓扑结构具有高动态性和不确定性， 此外计算复杂度也会随着网络规模呈指数级递增。针对这些问题，为有效计算φ（PSt Sw＋1( )），我们提出了一种基于前一步估算方法来近似评估当前服务恢复策略最小干扰强度，当服务路径上发生第一次失败时， 其节点的替代数目由一个近似的平均值E（NS）作为估计值。

设Lnk→nk＋1是服务链路sk［nk］→sk＋1［nk＋1］的预期生存时间，在时刻t Sw＋1的服务路径为PSt Sw＋1( )＝（s1［n1］→s2［n2］→…→sr［nr］），该服务路径的失败率估计为

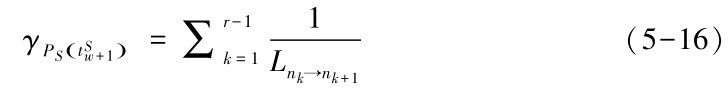
因此，φ（PSt Sw＋1( )）可近似估计为

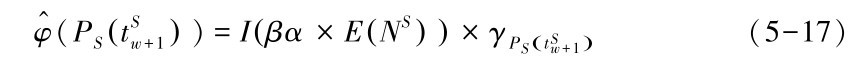
基于上述分析，将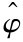（PSt Sw＋1( )）代入公式（14），得到面向服务覆盖层最小干扰的服务恢复策略解决思路：就是寻找服务路径PSt Sw＋1( )，使得服务组合失败干扰最小化：

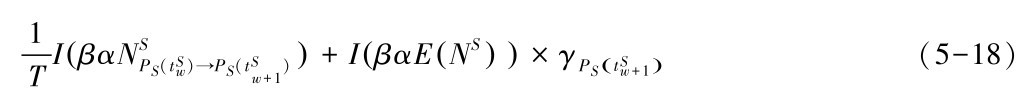
公式（5－18） 中，第一部分描述了服务恢复时间； 第二部分反映了新建服务路径的生命期， 最小化上式将会平衡这两方面的因素， 求得最优解。

本书给出一个启发式算法RHA来有效地进行服务路径的恢复。 该算法设计为两层： 分别是网络层重建NLRHA和服务层重建SLRHA。 底层网络恢复是由支撑当前服务路径的路由链路中断而发起的， 当网络层恢复成功时， 算法执行完毕； 若NLRHA无法恢复当前中断服务， 则启用服务层最小干扰恢复策略。 服务层恢复首先发现新的服务组件， 依据服务恢复干扰强度最小来实现服务替换方案， 接着完成组件之间底层网络物理链路的建立。