5.2.1 用户感知的服务中断干扰模型
VANETs下服务组合中断频繁发生， 如何能定量描述和测量服务中断对用户造成的影响， 使用户在服务执行期间感知干扰最小是设计服务重建算法的基本出发点。
以往研究中， 服务组合及重建中涉及的服务中断通常用服务可用性（Service Availability，SA） 来描述［130，133，134］，将服务可用性定义为服务生存时间 （Service Life Time， SLT） 内非中断有效执行时间所占的比率， 如公式（5－4）所示，其中，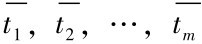
表示了一系列中断时间，m为服务中断次数，SLT为服务生存时间，
然而用服务可用性SA来描述服务中断， 存在着一定的问题：
第一， SA不能有效体现服务中断的频率。
SA描述的是服务生存期内有效服务执行时间所占的比率， 它并不能衡量高失效频率、 短中断间隔的场景和低失效频率、 长中断间隔的场景， 如图5.6所示，尽管场景1和场景2都有相同的服务可用性SA （SA＝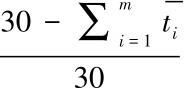
＝
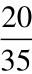）， 但用户体验的中断干扰却完全不同， 场景2的组合服务的频繁失败对用户的容忍度是一种考验。
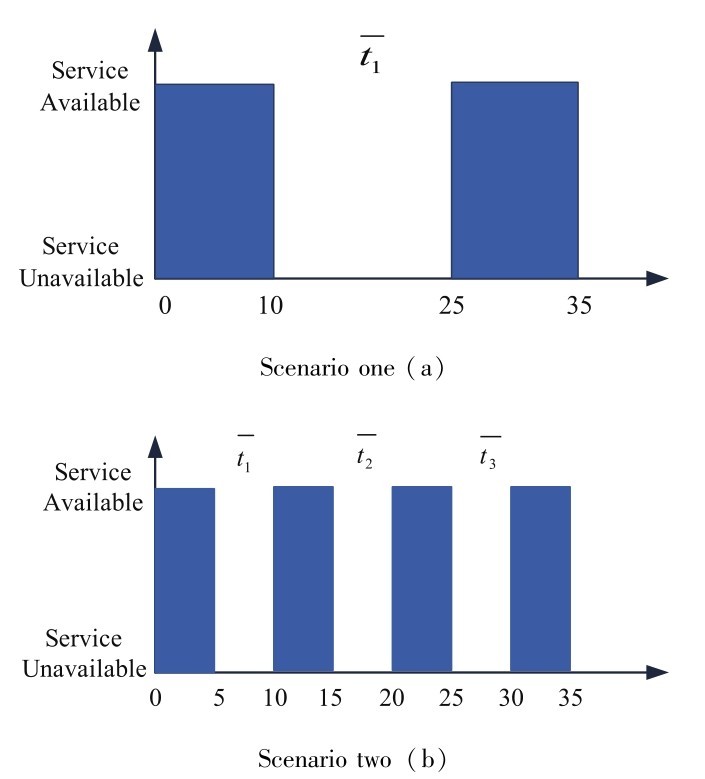
图5.6 不同的服务中断场景
第二， SA的理论分析虽然简单， 但对于实际计算却存在着一定的难度。
这是因为，SA是由一系列服务中断时间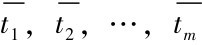
决定的，而这些中断时间往往受一些动态且不确定因素的影响， 如当前系统状况、 节点负载、网络拓扑结构、 路由策略等等， 尤其是在高动态网络环境中， 计算这一系列服务中断间隔， 是非常困难的。
为解决第一个问题， 有效描述服务中断频率对用户造成的影响， 本书参考一种健壮的效应函数映射关系I（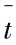
）来表达用户对于服务中断时间及中断发生频率的相对敏感度，共有三种基本类型［38，130］， 其中图5.7 （a） 表示用户感知的干扰同服务中断时间成线性关系， 用户容忍度一般， 属于中性； 图5.7 （b） 表示一种凸性的干扰函数， 用户不满意度随着中断时间增加会骤然提高，用户耐心不足， 尤其是对长时间的中断更无耐心； 图5.7 （c） 是一种凹性的干扰函数， 尽管用户不满意度随着中断时间的增加提升缓慢， 对于失败频率较为敏感。
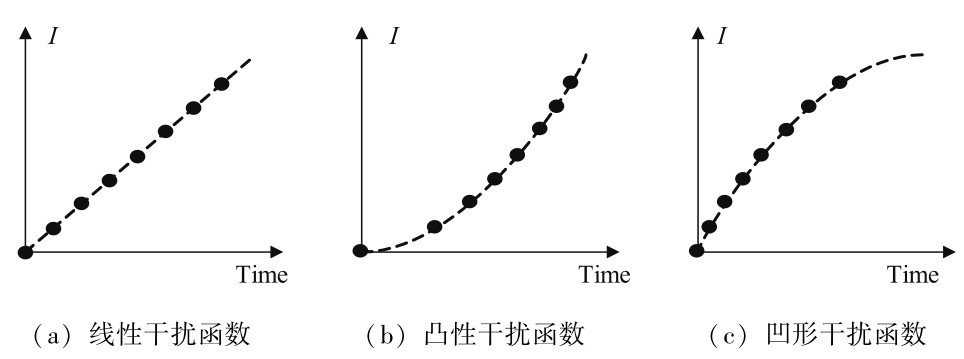
图5.7 三种基本的服务干扰函数
事实上， 从最初服务组合路径建立到执行结束， 对服务路径的恢复重建往往不止一次， 尤其是在VANETs节点快速移动情形下重建将会更加频繁。假设在第k次服务恢复过程中，服务节点替换数目为Nsub（k），为计算简便，我们令发现并替换单个服务节点的时间代价固定为Tre，通过效应函数映射对应用户感受的干扰值可表达为I（Tre·Nsub（k）），设M为服务执行完毕时服务路径重建的次数， 则该组合服务恢复过程对用户造成干扰的总和记作In
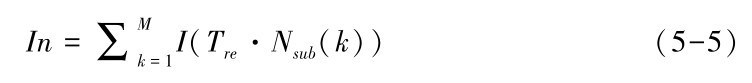
进一步， 我们将单位时间内用户感知的干扰值定义为干扰强度D， 用其描述服务中断时间和服务中断发生频率对用户造成的干扰， 其中T（k）表示第k－1次与第k次恢复的时间间隔，
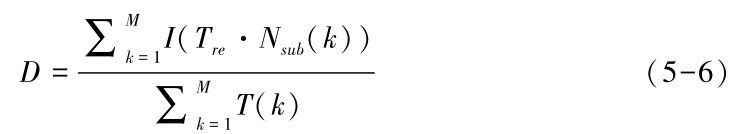
依据前面的介绍可知， 服务中断时间T（k）的计算是模型化服务中断的第二个难点， 原因在于中断时间间隔是由许多不确定的动态因素综合确定的（节点负载、 网络流量等）， 因此本书采用服务恢复时间估算的方式， 利用可用节点替换的频率和数量来估计服务的恢复时间， 进一步定义干扰强度。
考虑组合服务SC在时刻0实例化并在时刻T执行完毕， 设π为服务生存期内一系列服务组合路径的集合，π＝｛P（t1），P（t2），…，P（tl）｝，0＜t1＜t2…＜tl＜T，假设P（tv）是 tv，tv＋1[ ]期间的服务组合路径，从服务路径P（tv）恢复到服务路径P（tv＋1）服务中断时间
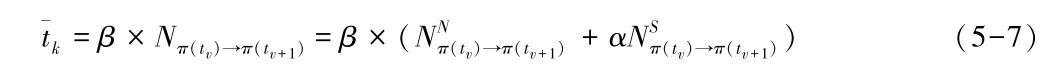
其中，NNπ（tv）→π（tv＋1）和NSπ（tv）→π（tv＋1）分别表示从服务路径P（tv）过渡到服务路径P（tv＋1）过程中网络层物理链路的替换数目和服务实例层服务组件的替换数目。β为将替换数目转化为中断时间的参数，α＞1表示服务组件替换恢复时间相对于网络链路替换中断时间的权重。
基于上述分析， 我们可将用户感知的干扰强度 （公式5－6） 可近似表达为
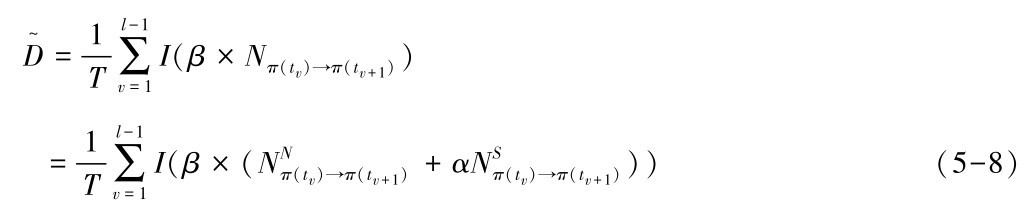
因此， 基于用户感知最小干扰的服务组合重建就是要在服务路径中断后，寻找满足用户需求的最优替换路径，使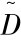
值最小。