3.3.3 基于跨层QoS的服务执行路径选择算法LOSPSA
服务执行路径选择问题就是要从多条满足用户功能需求的服务路径中选择一条非功能属性最优的路径作为最后的服务组合执行方案， 这是一个被证明了的NP完全问题［75，76，77］。研究表明，目前基于进化的智能优化算法是解决该问题的主要方法， 进化算法是模拟自然界生物进化机制而形成的自适应全局优化搜索算法， 被广泛地应用于求解组合问题， 但往往应用于传统静态网络下的服务组合优化问题［78，79］；在动态网络环境中尤其是在底层拓扑频繁变化的情况下， 进化算法求解的复杂度较高， 需要作进一步深入探究。 因此，我们采用两级打分 （2－level） 策略， 通过一种局部最优服务路径选择算法（Local Optimal Service Path Selection Algorithm，LOSPSA） 来确定服务执行路径， 大大提高服务执行效率。
首先，基于我们提出的支持服务覆盖层服务执行路径的QoS模型QVoverlay（s）＝（qav（Ps，t），qpr（Ps，t），qre（Ps，t），qde（Ps，t））来构建服务路径的服务质量参数评价体系， 确定可用性qav（Ps， t）、 价格qpr（Ps， t）、 可靠性qre（Ps，t） 和时延qde（Ps，t） 四个属性作为衡量服务路径性能优劣的指标。综上分析，我们建立M＝ qi，j[ ] （1≤i≤4，1≤j≤r） 参数评价矩阵，可表达为（省略时间t）：
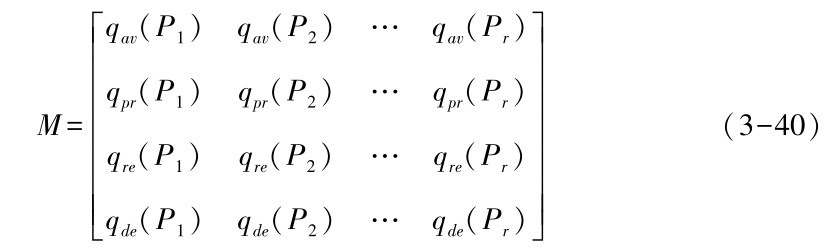
公式（3－40） 中，矩阵中的每一行表示不同服务路径的同一种服务质量属性，矩阵中的每一列对应可用服务路径集合Pf中的一条服务执行路径。
为简化起见， 我们将4种属性进行标度：
1＝qav，2＝qre，3＝qpr，4＝qde
化简后的服务质量参数矩阵M可表达为N＝（qij（Pj）；1≤i≤4，1≤j≤m）。 同时， 我们也定义QoS约束C， C为一个四维特征向量， 分别表示用户在可用性、可靠性、价格和时延四个方面的限定条件，表达为C＝ 〈c1，c2， c3，c4〉 ＝Q0。为统一不同QoS指标的度量单位，需要将不同类型的QoS属性进行标准化，使量化值在 ［0， 1］ 之间。 针对效益型属性 （数值越高， 服务质量越好） 和代价型属性［80，81，82］（数值越低，服务质量越好） 的区别，我们分别给出如下标准化公式：
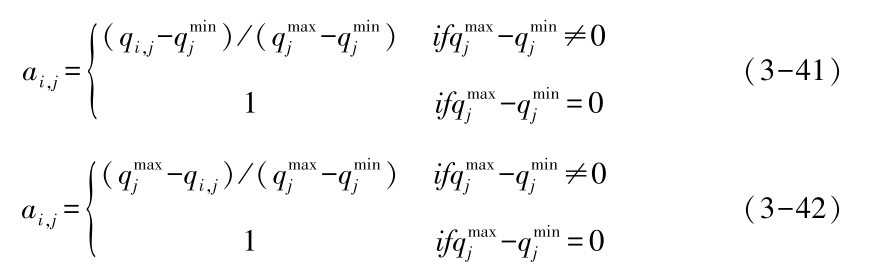
qmaxj ＝max（qi，j），1≤j≤m，为第i维属性的最大值；同理qminj ＝min（qi，j），1≤j≤m， 为第 i 维属性的最小值。 因此对服务质量参数矩阵 M＝(qij（pj）；1≤i≤4，1≤j≤r)运用上述公式标准化可得标准化矩阵 N＝ (aij（pj）；1≤i≤4，1≤j≤r)。
标准化工作结束后，我们对服务执行路径进行两级打分 （2－level）： 第一级打分是用户约束级别， 即过滤掉不满足用户某条件限制的服务执行路径，如延时不能超过20s； 第二级打分是筛选级别， 即对通过第一级测试的服务执行路径进行决策评估， 进一步打分。 两级打分之后选取得分最高者为服务执行路径选择问题的最终结果。 下面就第二级筛选的具体流程进行阐述。
对第一次过滤后的服务执行路径进行第二级筛选， 对其进一步打分， 最终由分数大小确定组合服务执行路径的性能优劣， 进而得到用户服务请求的响应。
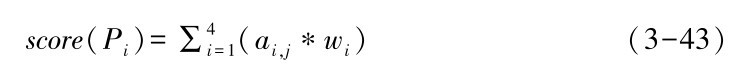
其中wi∈［0，1］∧∑4i＝1wi＝1，事实上不同用户对于不同的服务质量属性具有不同的侧重和偏好， 因而在第二级打分环节中一个关键环节就是设定每个QoS指标的权重。 权重的求解既要考虑用户主观感受还要考虑客观事实，因此我们采用多属性决策 （Multiple attribute decision making ， MADM） 理论［83，84］主、客观赋权相结合的方法求解服务质量属性的权重［85，86，87］，wi求解思路描述如下：
设wj是服务属性qj的权重，w·j∈w＝（w1，w2，…，wa）′，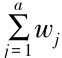
＝1，wj≥0，j＝1，2，…，a，对应可用服务路径集合Pf＝{Ps1，Ps2，…，Psr}，r∈N，即∀Psi，Psj∈Pf，若Psi▷Psj，当且仅当Biw·≥Bjw·，w·＝（w1·，w2·，…， wa·）′，i，j＝1，2，…，n，B是基于QoS参数矩阵的标准阵，B＝ [bij]n×m，即B＝（B1，B2，…，Bn）′，b·j ＝max{b1j，b2j，…，bnj}。D＝ d[ kj]m×m是属性比较矩阵，满足dkj≥0，dkj＝1/dkj，dkk＝1，dkj≈wk/wj，k，j＝1，…，m，其中dkj表示属性qk较属性qj的相对重要程度。
经过上述分析，wj可由如下公式确定权重值：
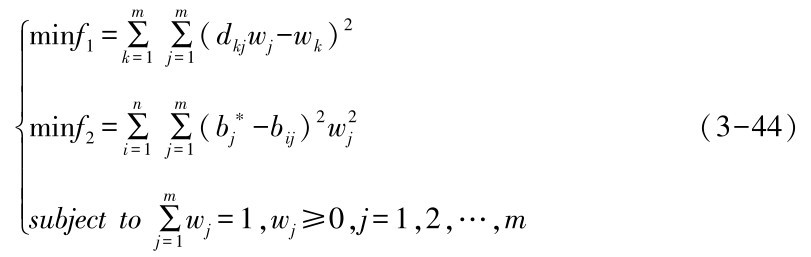
求解过程如下。 为求解模型构造如下多目标规划：
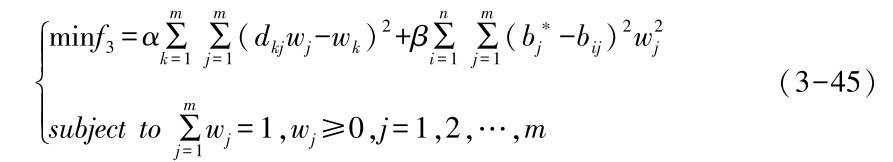
其中α， β表示主客观赋权模式相对重要程度， 并且满足
α＋β＝1，0＜α，β＜1 （3－46）
暂不考虑对m个权 （wj≥0， j＝1，2， …， m） 的非负约束， 构造Lagrange函数：
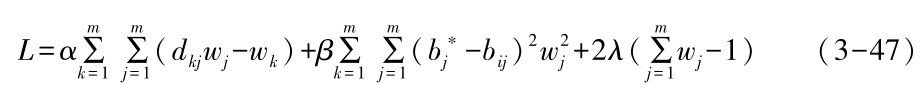
其中λ是Lagrange函数，设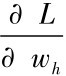
，1，2，…，m，则
Z＝ zij[ ]m×m，w＝（w1，w2，…，wm）′，e＝（1，1，…，1）′，O＝（0，0，…，0）′， Z的元素形式为：
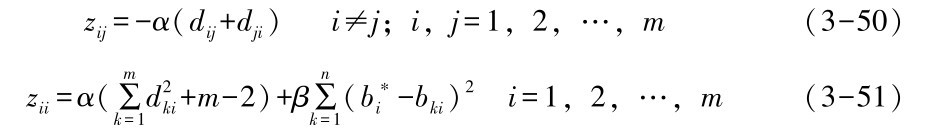
求解方程 （40）， 可得：
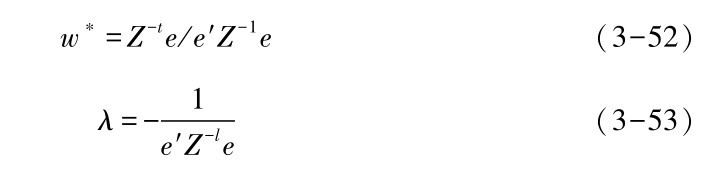
其中w∗就是主客观模式确定的权值。至此，依据公式score（Pi）＝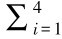
（ai，j×wi），第二级筛选结果可得。值得注意的是，如果第二次打分之后的候选执行路径仍不止一条， 我们会采用进一步的最优服务淘汰机制进行决策： 通过比较服务执行路径上服务提供节点与服务请求节点的相对距离来进行过滤， 将距离最小的服务路径作为用户请求的响应返回给用户。 在提出服务路径选择算法LOSPSA之前， 首先给出服务比较、 排序的相关概念。
定义3.20 （弱序关系“▷” ）：
设“▷” 为服务路径候选集PC＝[P1，P2，…，Pr]上的弱序关系，则满足弱序关系“▷” 的服务路径集合PC具有如下特性：
①连通性：∀Pi，Pj∈PC，Pi▷Pj，或Pj▷Pi，或两者都满足；
②传递性：∀Pi，Pj，Pk∈PC，Pi▷Pj且Pj▷Pk，则Pi▷Pk
③无差异性：Pi≅Pk当且仅当Pi▷Pj且Pj▷Pi
④等价性：若存在实值序列价值函数f，∀Pi，Pj∈PC，则f （Pi） ≥f （Pj） ⇔Pi▷Pj
基于2⁃level打分策略， 我们提出服务路径选择算法LOSPSA， 算法实施步骤如表3.3所示：
表3.3 服务路径选择算法
续表
