1.2.1 裂隙水流运动特征研究进展
一般而言，裂隙水流运动可以用纳维-斯托克斯方程（Navier-Stokes Equations，简称N-S方程）来描述。对于不可压缩黏性液体，非稳定流状态下，以矢量形式表示的N-S方程为
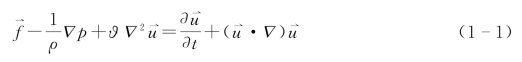
式中 ρ——流体密度；
p——压力；
ϑ——流体运动黏度；
——流速矢量；
t——时间；
——质量力；
∇——梯度算子。
其中，等号左侧为外力项，依次为：质量力项、压力项、黏性力项；等号右侧为加速度项，依次为当地加速度和迁移加速度。
由于N-S方程解的复杂性，在进行实际工程问题计算时，往往要借助于高速、大容量计算机，限制了方程的应用。为此，许多研究者按照水流运动实际情况，对N-S方程进行了不同程度的简化。
（1）第一程度简化。第一程度的简化将N-S方程简化为斯托克斯方程。简化条件为：惯性力可以忽略，即流速较小，黏性力占主导地位，雷诺数Re较小，此时，N-S方程可简化为
式（1-2）称为斯托克斯方程或者蠕动流方程。对于斯托克斯方程的具体应用条件，众多研究者进行了侧重面不同的研究。惯性力与黏性力之比可以用Re来表达，Re小意味着黏滞力的作用大，对液流质点运动起抑制作用，Re小到一定程度，水流呈层流状态；反之，水流呈紊流状态。对于单裂隙而言，Re计算式为
式中 lv——黏性力的特征长度；Ui——惯性力的特征流速；
μ——动力黏滞系数。
对于具有矩形过水断面的闭合单裂隙而言，Ui为流经裂隙的流量Q与过水断面bW之比，故对应于具有矩形过水断面闭合单裂隙的Re计算式为
式中 W——裂隙宽度；
b——裂隙开度。
对于光滑闭合平行单裂隙，由式（1-4）计算的判别层流、紊流流态的临界雷诺数为1200。
Sharp，Iwai以及Schrauf利用野外裂隙样本通过实验室试验分析得到，当Re大于1～10的某个数值时，惯性力不可以忽略不计。
Schrauf，Hasegawa利用扰动分析对裂隙开度按正弦变化的裂隙进行了一维模拟，提出利用斯托克斯方程估算N-S方程计算裂隙渗流量的修正系数，该修正系数与正弦裂隙开度b的振幅A、波长∧b以及Re有关。Zimmerman提出当Re（b）/∧b＜8时，惯性力对渗流量修正系数的影响最高达10%。
（2）第二程度简化。虽然与N-S方程相比，斯托克斯方程有了很大程度的简化，但是三维斯托克斯方程的解仍然非常复杂，实际情况中很少被应用。于是，众多研究者对斯托克斯方程进行了进一步的简化，即对N-S方程进行了第二程度的简化。简化条件为裂隙面起伏变化平缓，裂隙开度变化不大，那么垂直于裂隙面的流速分量可忽略不计（即un=0），黏滞力主要表现为垂直于裂隙面的剪切力
，假设裂隙面垂直于z轴，由此得出二维斯托克斯方程：
联合裂隙面处流速为零方程，式（1-5）可进一步写成：
式（1-6）称为局部立方定律（Local Cubic Law，LCL），同时也是雷诺方程（Reynolds Equation）的一种简化形式（裂隙面静止，运动黏度为常数）。雷诺方程假设流速分布呈抛物线形分布，即著名的泊肃叶定律（Poiseuille Law）。假设水流沿x轴流动，设x轴位于两裂隙面的中间
处，因此沿x轴方向的流速分布为抛物线分布，即
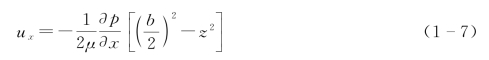
大量学者对于雷诺方程的适用条件从理论、数值模拟以及试验等方面进行了研究。
1991年，Zimmerman等提出当∧b至少是σb的5倍时，由局部立方定律估计斯托克斯方程的误差最大为10%。1996年，Zimmerman和Bodvarsson指出当Re＜1时惯性力可忽略。2000年，Zimmerman和Yeo发现当∧b是b的2.6～3.3倍时，由局部立方定律估计斯托克斯方程的误差最大值为10%。
Koyama等利用有限元仿真软件COMSOL Multiphysics对二维粗糙裂隙分别应用N-S方程和雷诺方程进行了裂隙流稳态模拟，得出利用雷诺方程模拟得到的裂隙渗流量超出利用N-S方程所得裂隙渗流量的5%～10%，并且在粗糙裂隙中抛物线形的流速分布不再适用。
Brown等，Zimmerman和Bodvarsson，Ge指出如果想维持抛物线形的流速分布（即垂直于裂隙面的水力坡度可忽略不计），裂隙张开度的均值和方差必须比裂隙张开度变化的特征长度小得多。
1991年，Glass等利用激光轮廓测定法和光吸收法对尺度为30cm×15cm的模型裂隙进行了裂隙张开度测量。并指出雷诺方程模拟得到的水力开度大约等于由试验测得的平均开度。1993年，Reimus等对尺度为11.6cm×10.4cm的野外裂隙样本做了研究。研究结果表明，由雷诺方程模拟得到的水力开度远远大于由试验测得的平均开度。1999年，Nicholl等对粗糙裂隙中雷诺方程的适用性进行了研究，结果表明，由雷诺方程模拟得到的水力传导度和由试验测得的水力传导度偏差达到22%～47%；同时指出用三维描述粗糙裂隙水流的重要性。
（3）第三程度简化。对N-S方程进行第三程度的简化，简化条件为两裂隙面光滑且平行分布（即uy=uz=0），则三维的流体流动可概化为一维流动，设流体沿x轴流动，则沿x轴方向的裂隙渗流量为
式中 Q——裂隙间的流量；
b——裂隙开度；
J——水力坡度；
C——常数。
式（1-8）由于流量Q与裂隙开度b的三次方呈正比，故称为立方定律（Cubic Law）。
对于直线流，常数C可表达为
由式（1-8）和式（1-9），可得裂隙渗流量方程为
式中 W——裂隙宽度；
L——裂隙开度；
ρ——流体密度；
g——重力加速度；
μ——动力黏度。
对于径向流，常数C可表达为
式中 re、rw——裂隙面的外径和内径。
裂隙渗流量又可表达为
而水力坡度与水头损失之间的关系为
式中 J——水力坡度；
v——裂隙间的水流流速；
hf——水流流经裂隙时的水头损失。
将式（1-12）、式（1-13）代入式（1-10），得到层流状态下开放平行裂隙中立方定律的另一种表达形式为
式（1-14）表明，恒温条件下，水流流经开放平行光滑裂隙时的水头损失与水流流速呈线性关系。
由于立方定律形式的简洁性，大量学者习惯用立方定律来描述裂隙水流运动，但是由于立方定律有很大的局限性（适用于层流状态下，平行、光滑、开放裂隙中的水流），为此，国内外许多学者对立方定律进行了验证，并根据自己的研究对象和成果提出了修正立方定律的不同形式。
1951年，Lomize利用平行开放玻璃板模拟裂隙，验证了层流状态下立方定律的有效性，同时Lomize研究了光滑裂隙面、粗糙裂隙面以及不同形状的裂隙面组合（上下裂隙面呈波状变化上下对称，上下裂隙面呈波状变化上下吻合）对裂隙渗流的影响，并提出了层流和紊流状态下相应的裂隙渗流量计算式。
层流：
紊流：
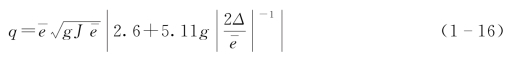
式中 q——单宽流量；
Δ——裂隙粗糙度；
——裂隙平均开度。
1966年，Romm对微裂隙（10～100μm）和极微裂隙（0.25～4.3μm）进行了试验研究，研究结果表明立方定律在微裂隙及极微裂隙中都是有效的，同时作者指出裂隙开度小至0.2μm时，立方定律仍然适用。
1969年，Louis独立进行了与Lomize相似的试验并得到了与Lomize得出的公式形式类似但系数不同的裂隙渗流量计算式。
层流：
紊流：
1970年，Sharp，1972年Sharp和Maini基于裂隙有效开度提出了经验流量公式，对立方定律提出了质疑，并指出立方定律中的指数“3”应该为“2”。基于以上观点，1975年，Gale指出如果按照实际研究的裂隙开度来计算裂隙渗流量，立方定律仍然是适用的。
1976年，Iwai利用室内试验研究了裂隙接触面积对裂隙渗流的影响，提出渗流量计算式。
式中 Q——对应于接触面积率为ω时的流量；
Q0——对应于ω=0时的流量；
ω——裂隙面面积接触率；
φ——经验系数。
之后1981年，Walsh模仿热传导理论提出φ=1。1996年，周创兵通过数学推导得到φ=0。
1985年，Barton通过大量试验提出节理粗糙度系数法JRC修正立方定律，将等效水力开度bh与力学开度bm联系起来，
，用bh代替立方定律中的开度即可得到修正立方定律，该方法的关键点在于如何获取节理粗糙度系数JCR，计算式为
1980年，Witherspoon等验证了不同的裂隙面类型（花岗岩、玄武岩、大理石），不同裂隙开度（4～250μm）条件对立方定律有效性的影响，研究结果表明，立方定律在裂隙开度为4～250μm的裂隙中仍然有效，且与裂隙面类型无关，同时Witherspoon等提出可以由裂隙面特征系数（f，其数值在1.04～1.65之间）来表征所研究裂隙与理想裂隙之间的差别，并用
代 替式（1-8）中的常数C来计算所研究裂隙的渗流量。
1981年，Neuzil提出裂隙开度密度分布函数n（b）修正法，该方法假设裂隙开度沿垂直水流方向变化，而沿水流方向不变，通过数学推导得到裂隙渗流量表达式为
1981年，Tsang考虑了裂隙样品尺寸效应的影响，将式（1-21）推广到二维裂隙面情况，并得到裂隙渗流量表达式为
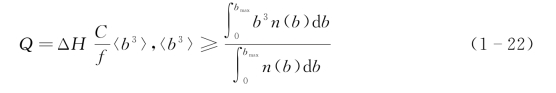
如果裂隙开度函数是已知的，则可以直接用裂隙开度函数来修正，但是在实际情况中，裂隙的开度函数是很难量测的，因此，Elsworth和Goodman提出用标准正弦曲线或锯齿形曲线近似表征裂隙壁面的几何形状，然后根据裂隙壁面发生压缩或错位的程度得到裂隙开度函数。由于裂隙开度函数的难获得性，这一方法较为有效。
1994年，Amadei和Illangasekare以数值方法生成的粗糙裂隙为研究对象，利用数值计算得到裂隙面渗流的经验公式为
1995年，速宝玉以人工粗糙面裂隙为研究对象进行室内物理模型试验，在Lomize和Louis研究结果的基础上提出了裂隙面的渗流公式为
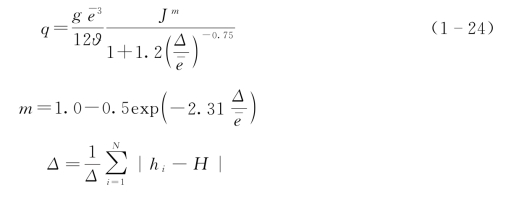
式中 hi——测点高程；
H——平均高程。
1997年，王媛等对粗糙裂隙渗流特性进行了数值模拟，提出对于张开裂隙，可以近似用平均开度代替等效水力开度，但是对于有部分接触的裂隙则不能进行简单的代替，而是要用式（1-19）来计算。
2000年，潘国营和韩星霞以裂隙开度为2～8mm的3种不同粗糙程度的人工缝隙（光滑、中粗、粗糙）为研究对象，利用室内模拟试验，研究了水流流态对水流运动方程的影响，研究结果表明，当Re超出200～700时，水流流速与水力坡度之间呈非线性关系，立方定律不成立。
2003年，许光祥等首次提出超立方（裂隙单宽流量与平均开度之间的方程幂指数大于3）和次立方（裂隙单宽流量与平均开度之间的方程幂指数小于3）的概念，并通过试验来研究超立方定律和次立方定律是否存在，结果表明超立方定律和次立方定律在粗糙裂隙的渗流中可能同时存在。其认为超立方定律和次立方定律的初步判别标准为：壁面为吻合粗糙的裂隙流符合次立方定律，壁面为非吻合粗糙的裂隙流符合超立方定律。
2006年，张柬等选取天然裂隙岩体为研究对象进行试验研究，并对试验数据进行了拟合，单宽流量与平均开度之间、单宽流量和裂隙面相对粗糙度之间的拟合公式分别为
式中 m——取值为2.64～3.55；
a——取值为7.1～41.4；
d——取值为-3.1～3.5。
同时张柬等研究结果表明，天然岩体裂隙的渗流不完全符合立方定律，并证实了超立方定律和次立方定律的存在。单宽流量与裂隙面相对粗糙度之间存在正相关（b＞0）和负相关（b＜0）两种情况。
2010年，卢占国等利用自制的裂隙介质试验装置，对张开度为50～300μm的平行裂隙进行了一系列流动试验研究，得到了粗糙平行裂隙单宽流量经验公式及非线性渗流开始时的临界速度公式为
式中 k——裂隙渗透率；
l——裂隙长度；
A——裂隙截面面积；
vc——临界流速。
综上所述，裂隙中的水流运动可以用N-S方程来描述，但是由于该方程解的复杂性以及对计算机性能的高要求，使得其应用受到限制。于是众多研究者按照水流运动实际情况，对N-S方程进行了3种不同程度的简化；第一程度的简化适用于流速较小时的斯托克斯方程；第二程度的简化适用于裂隙面起伏变化平缓，裂隙开度变化不大，流速较小时的雷诺方程；第三程度的简化适用于2个光滑平行面间流速不大的流体的立方定律。对N-S方程简化为斯托克斯方程，研究者主要从Re出发，研究了其适用条件。对斯托克斯方程进一步简化为雷诺方程，研究者基于裂隙张开度从理论、数值模拟以及试验等方面研究了其适用条件，相对于立方定律适用条件的研究，对斯托克斯方程和雷诺方程适用条件的研究者相对较少，这不仅是因为立方定律表达的简洁性，而且因为立方定律的广泛应用性。综合国内外研究成果，研究者对立方定律的适用条件，主要从裂隙开度分布函数修正法、裂隙开度函数直接修正法、裂隙壁面粗糙性修正系数修正法、节理粗糙度系数修正法、面积接触率等方面进行了研究，并基于各自的研究对象提出了立方定律的修正形式。然而，以往的研究者绝大多数注重于开放裂隙中立方定律的应用，而在实际野外地区，完全开放的裂隙（2个裂隙面组成）是不存在的；相反，闭合裂隙（4个裂隙面组成）广泛存在。针对这一问题，本书对过水断面为矩形的闭合平行裂隙中立方定律的有效性进行研究，提出以极限流速以及极限雷诺数Relim来衡量立方定律是否适用，基于研究成果提出了适用于闭合平行裂隙的修正立方定律，并对裂隙流的水力特性进行了研究，该研究不仅对以往的理论研究进行了一定补充，而且为裂隙网络-管道双重介质水流运动特征的研究提供理论支撑。