4.3.4　落水洞水位与泉流量关系分析

4.3.4　落水洞水位与泉流量关系分析

4.3.4.1　基于泉流量线型的落水洞水位预测

设置7个不同的含水层初始饱和厚度（H0=86.0cm，76.0cm，65.5cm，55.0cm，44.5cm，34.0cm，23.5cm），每次试验中，水流排泄至排泄水箱，排泄水箱连接压力传感器，试验过程中记录排泄水箱水位变化。排泄水箱水位随时间变化，如图4-32所示。

设排泄水箱中水位随时间变化为

则排泄水箱中水的体积随时间变化为

对式（4-26）取微分，泉流量随时间变化计算式为

式中　S——排泄水箱横截面面积，cm2。

由Matlab程序处理可得，不同含水层初始饱和厚度条件下，泉流量衰减曲线，如图4-33所示。

经回归分析发现，含水层初始饱和厚度与泉流量线型即初始流量Q0及衰减系数α有密切的关系。记为

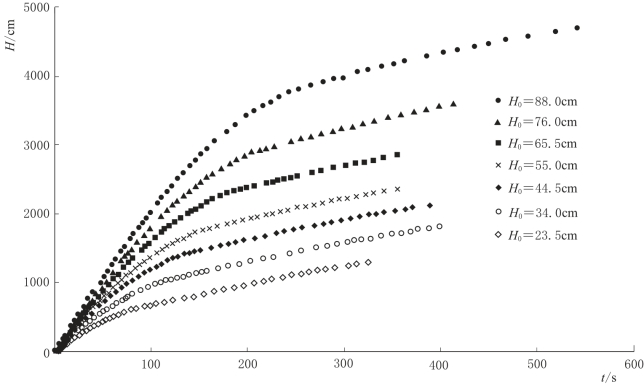
图4-32　排泄水箱水位变化曲线图

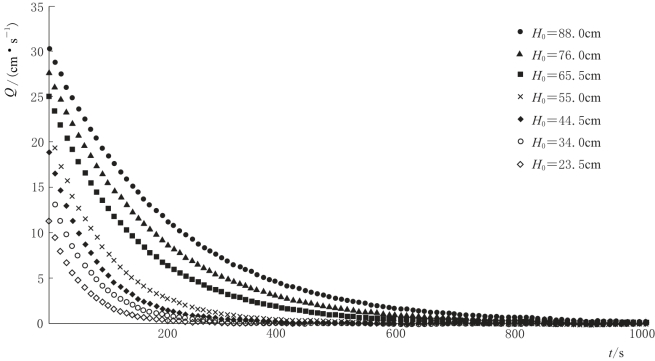
图4-33　泉流量衰减曲线图

回归分析所得参数值及其置信区间，见表4-7。数学模型计算值与物理试验测量值对比，如图4-34所示，从图中可以看出，计算值与试验值的对比点都在直线y=x附近，数学模型计算值与物理试验测量值吻合度较高。

表4-7　回归分析结果一

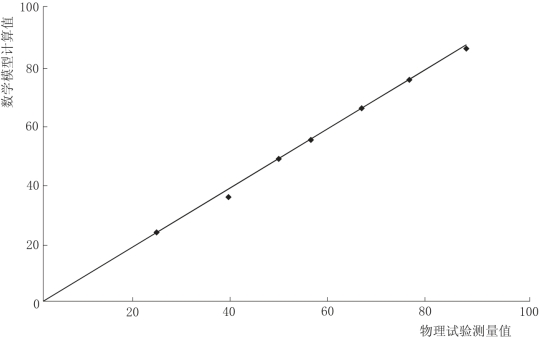
图4-34　数学模型计算值与物理试验测量值对比图

4.3.4.2　基于落水洞水位的泉流量预测模型

设泉流量变化方程为

初始流量Q0以及衰减系数α与含水层初始饱和厚度H0以及含水层中水的储存量V密切相关，即泉流量变化计算式为

由回归分析可得，初始流量Q0与含水层初始饱和厚度H0以及含水层中水的储存量V之间的函数关系f（M，V）为

同理，由回归分析可得，衰减系数α与含水层初始饱和厚度H0以及含水层中水的储存量V之间的函数关系g（M，V）为

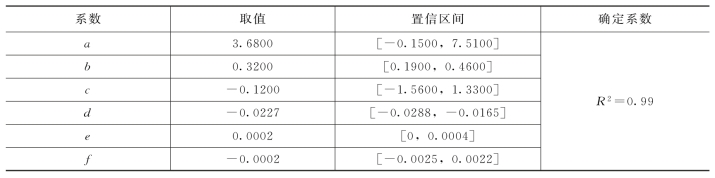
回归分析结果所得系数值及其置信区间，见表4-8。

表4-8　回归分析结果表二

初始流量Q0以及衰减系数α的数学模型计算值与物理试验测量值对比，如图4-35所示，从图中可以看出，两者对比点都在直线y=x附近，吻合度较高。

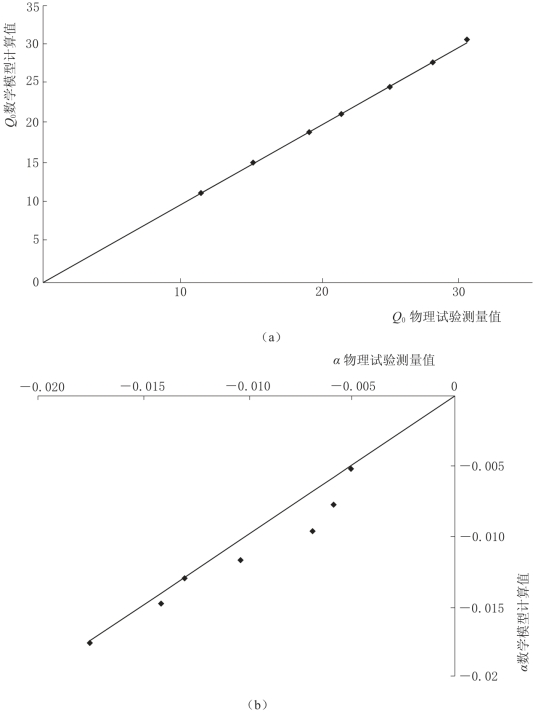
图4-35　初始流量Q0以及衰减系数α的数学模型计算值与物理试验测量值对比图