4.3.2 落水洞水位对水文情景二的响应变化
水文情景二中设置7个不同的含水层初始饱和厚度,对应每一个含水层初始饱和厚度,设置6个不同的泉口大小,主要研究落水洞水位对不同含水层初始饱和厚度及不同泉口大小的响应变化。
4.3.2.1 含水层倾角为0°
分析试验结果,得到不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化如图4-19所示。
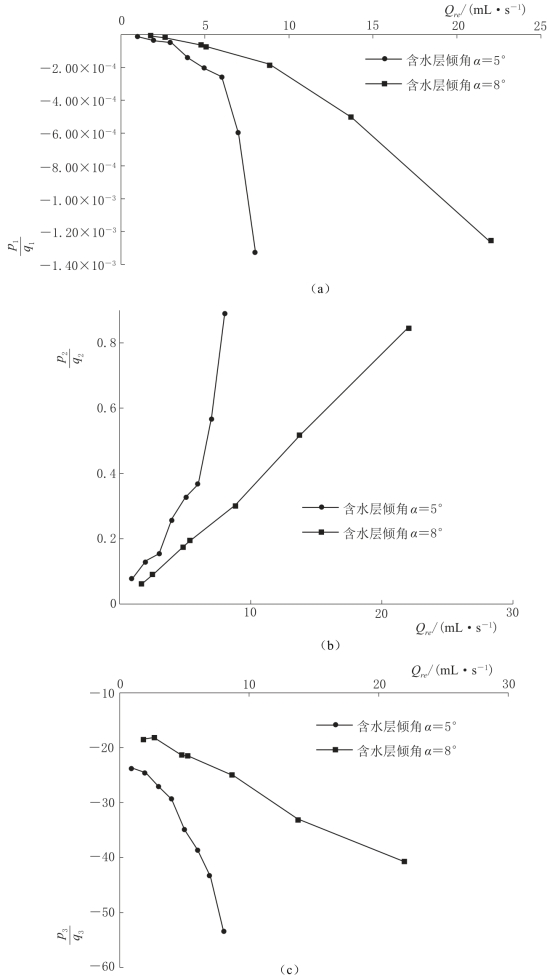
图4-18 不同含水层倾角条件下,落水洞水位二次函数表达式系数随补给强度变化曲线图
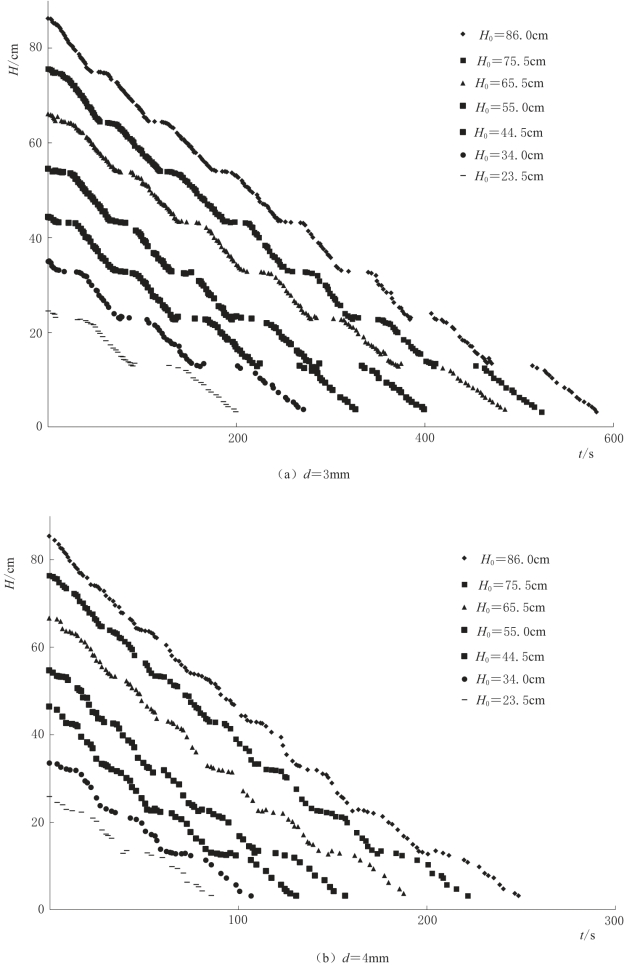
图4-19(一) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=0°)
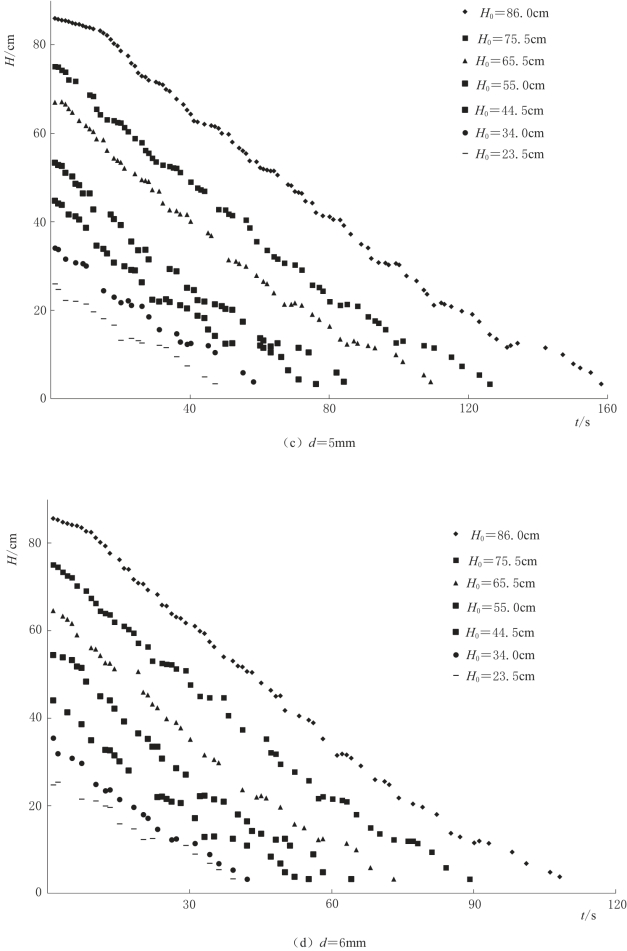
图4-19(二) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=0°)
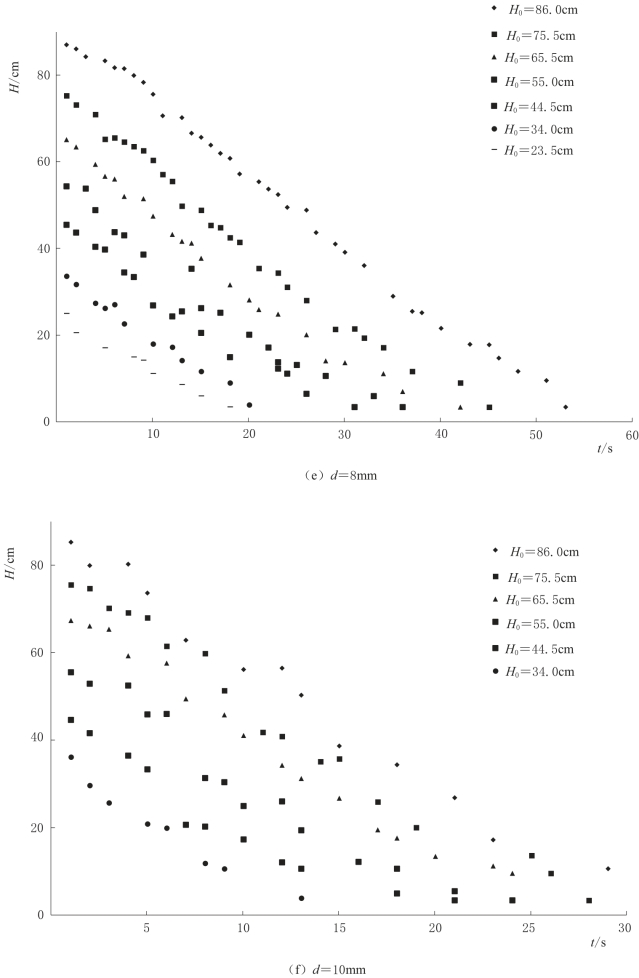
图4-19(三) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=0°)
在只有排泄,没有补给的试验条件下,不同泉口大小条件下,落水洞水位随时间呈阶梯状下降,如图4-19(a)~(c)所示,水位下降呈阶梯状主要受横向裂隙影响,流入垂向裂隙的水,汇集至层面裂隙,相比在垂向裂隙中的水流,在横向裂隙中的水流流速减慢,而且有一部分水流入落水洞,经过层面裂隙的过渡,使得落水洞水位间断性下降变缓,即表现为图中的阶梯状,而且图中阶梯个数(7个)与层面裂隙条数(7条)一致,也验证了以上解释的正确性。而且这一过程在试验过程中也可以观测到。然而随着泉口的增大,水位下降的阶梯状越来越不明显,甚至消失,这是由于泉口增大,水流流速增大,水位下降速率增大,弱化了层面裂隙的过渡作用。
图4-19中对应每一个泉口大小,不同含水层饱和厚度条件下,除含水层初始饱和厚度不同,水位下降曲线斜率大致相同。在此次研究中,每一条曲线由直线概化,计算式为
![]()
式中 H——落水洞水位,cm;
t——时间,s;
H0——含水层初始饱和厚度,cm;
C0——系数,下角标0对应含水层倾角为0°,cm/s。
系数C0的大小与泉口大小d变化密切相关,如图4-20所示。经曲线拟合可得:
![]()
记C0=g(d)0,因此,
![]()
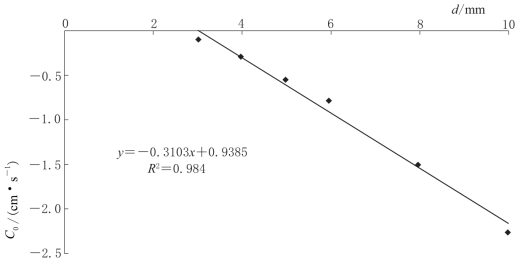
图4-20 系数C0与泉口大小d的相关关系曲线图(α=0°)
4.3.2.2 含水层倾角为5°
含水层倾角为5°时,分析试验数据,得到不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化如图4-21所示。
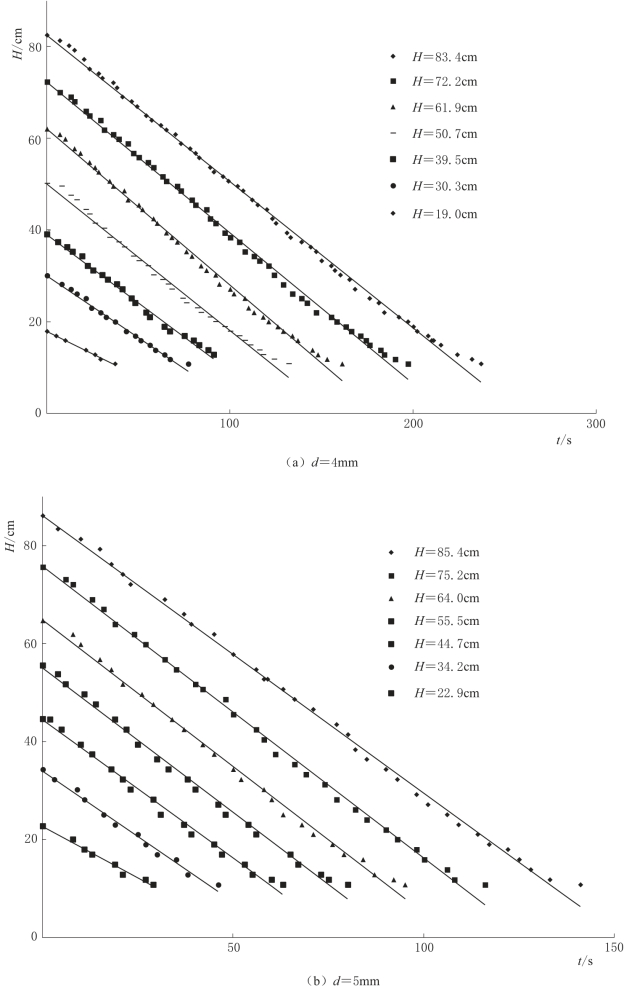
图4-21(一) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=5°)
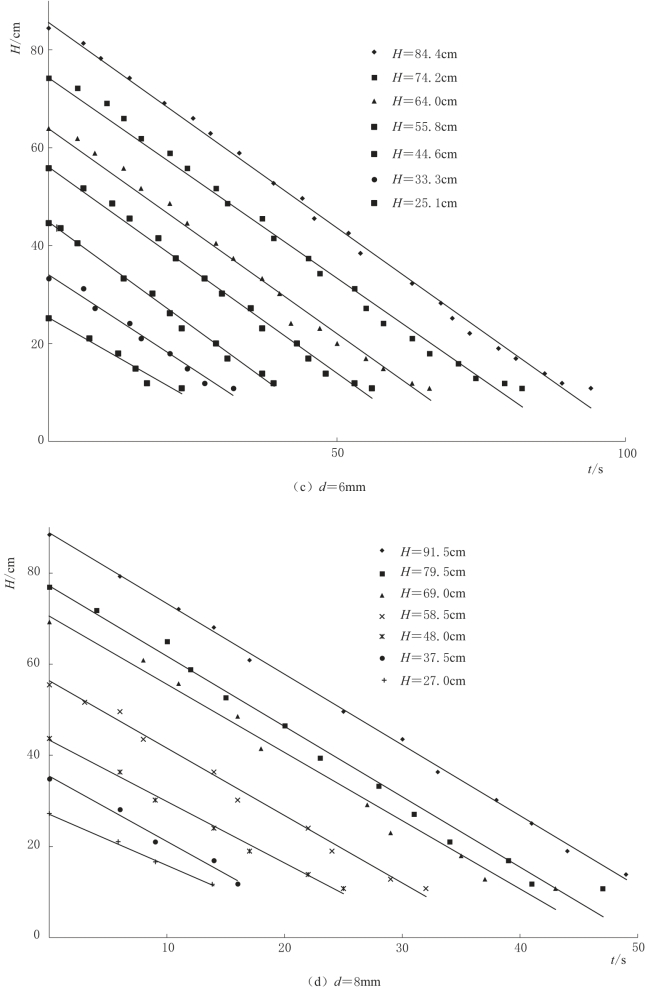
图4-21(二) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=5°)
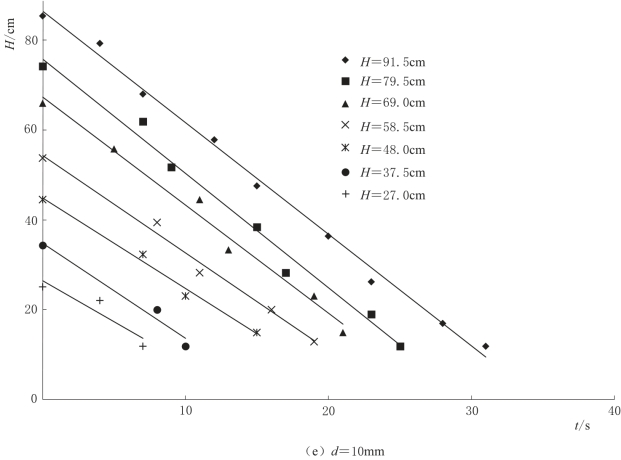
图4-21(三) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=5°)
研究结果表明,不同泉口大小条件下,落水洞水位随时间均呈直线变化。在同一含水层初始饱和厚度下,泉口越大,水位下降速率越快。在同一泉口大小条件下,不同含水层初始饱和厚度的大小对水位下降速率影响不大,可由有相同斜率的一族直线描述,设为
![]()
式中 H——落水洞水位,cm;
t——时间,s;
H0——含水层初始饱和厚度,cm;
C5——系数,下角标5对应含水层倾角为5°,cm/s。
系数C5的大小与泉口大小d变化密切相关,如图4-22所示。经曲线拟合可得(https://www.daowen.com)
![]()
记C5=g(d)5,因此,
![]()
4.3.2.3 含水层倾角为8°
含水层倾角为8°,分析试验数据,得到不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化,如图4-23所示。
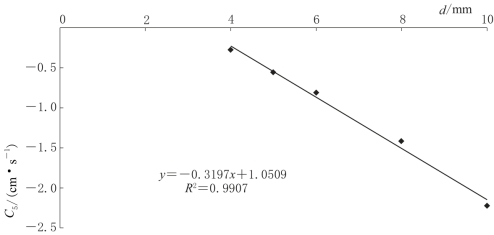
图4-22 系数C5与泉口大小d相关关系曲线图(α=5°)
含水层倾角为8°条件下,落水洞水位下降特征与含水层倾角为5°条件下落水洞水位下降特征类似,此处不再赘述。
含水层倾角为8°时,落水洞水位变化方程设为
![]()
式中 H——落水洞水位,cm;
t——时间,s;
H0——含水层初始饱和厚度,cm;
C8——系数,下角标8对应含水层倾角为8°,cm/s。
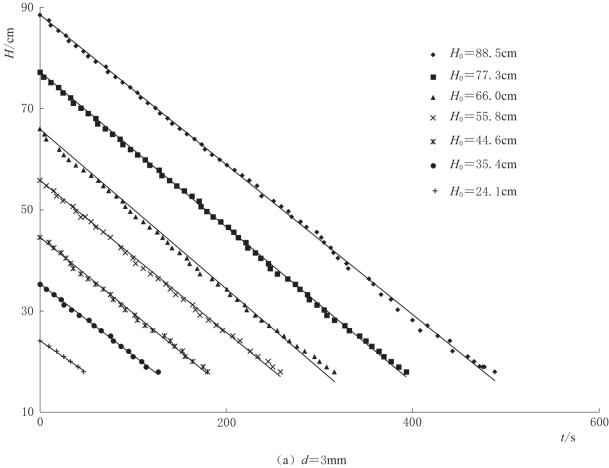
图4-23(一) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=8°)
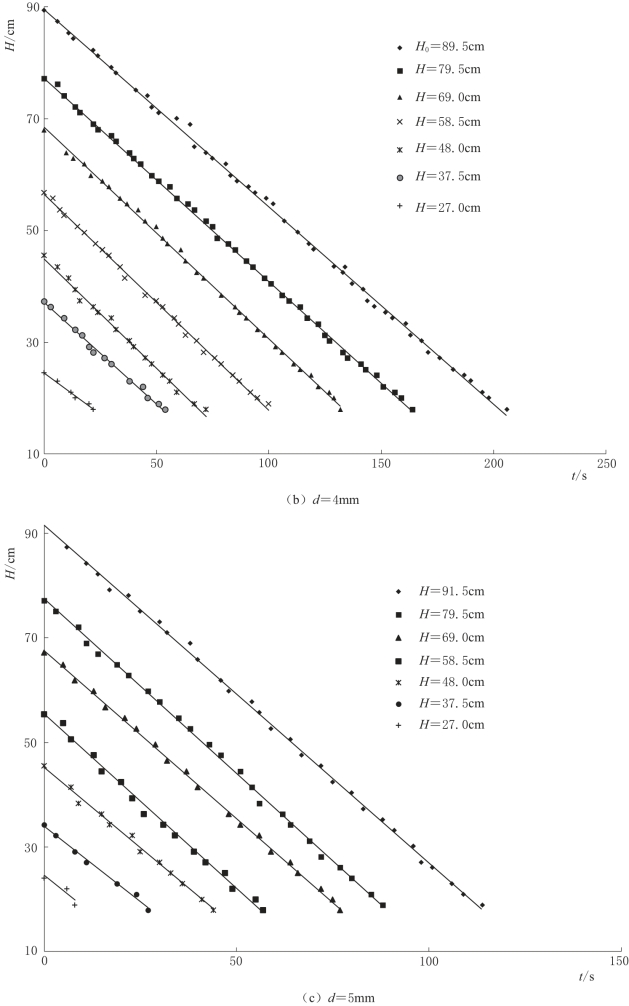
图4-23(二) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=8°)
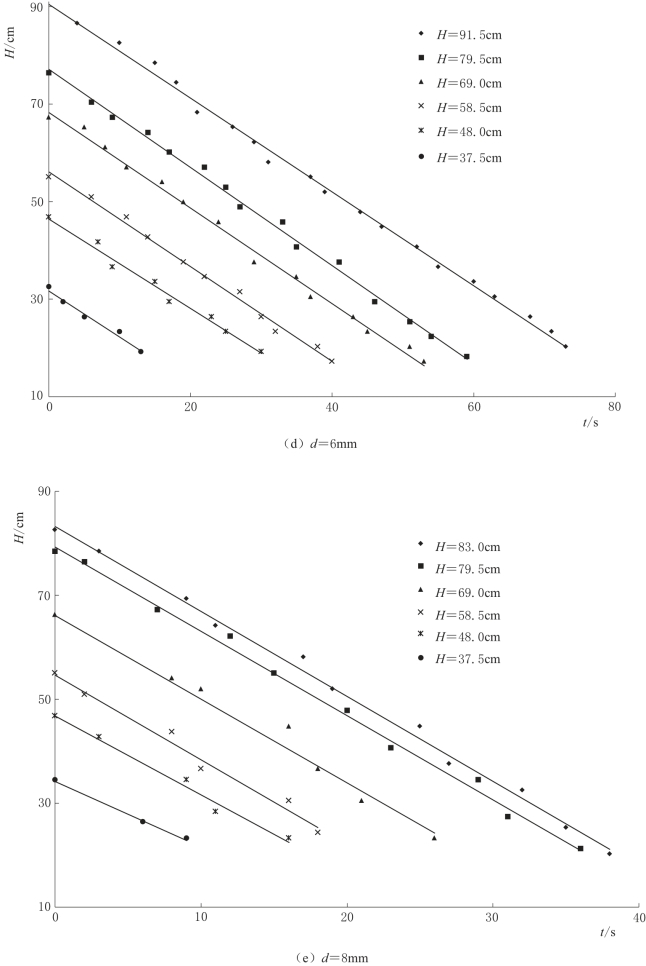
图4-23(三) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=8°)

图4-23(四) 不同泉口大小条件下,落水洞水位对含水层初始饱和厚度的响应变化曲线图(α=8°)
系数C8的大小与泉口大小d变化密切相关,如图4-24所示。经曲线拟合可得
![]()
记C8=g(d)8,因此,
![]()
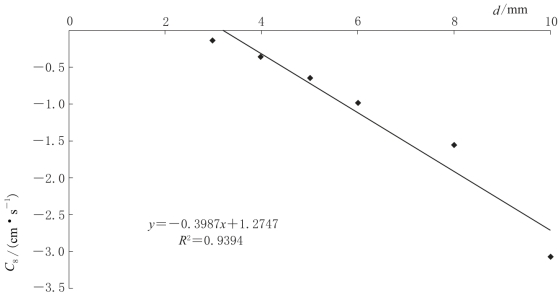
图4-24 系数C8与泉口大小d相关关系曲线图(α=8°)
4
.3.2.4 对照试验
对照试验中,由有机玻璃制成的直径为24.2cm的圆形玻璃桶代替裂隙网络-管道含水介质,设置4个不同直径的泉口(d=3mm,4mm,5mm,6mm)。相同的试验操作,试验结果如图4-25所示。从图4-25中可以看出,不同泉口大小条件下,水位随时间呈直线变化,且泉口越大,水位下降速率越大。水位变化可由式(4-20)表达,式中H0及Qdis均为定值。

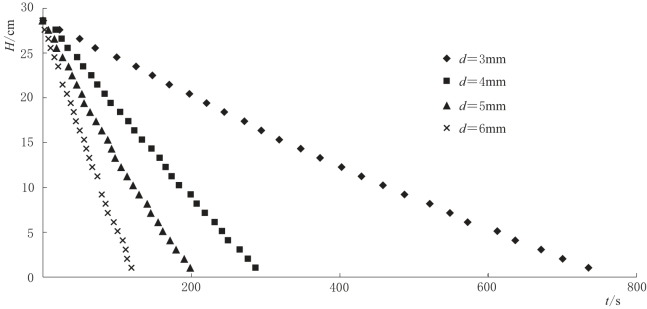
图4-25 水文情景二对照试验结果图
4.3.2.5 结果对比分析
首先分析3组试验结果的相同点:无论含水层有无倾角,不同泉口大小条件下,含水层初始饱和厚度对落水洞水位的下降影响较小。同一泉口大小条件下,落水洞水位随时间变化曲线可有一族有相同斜率,不同截距(即含水层初始饱和厚度)的直线H=Cit+H0刻画,系数Ci与泉口大小d之间可由直线描述,且泉口越大,水位下降速率越大。对比分析不同含水层倾角条件下,水位下降速率与泉口之间的相关关系,如图4-26所示。从图中可以看出,当泉口较小时,落水洞水位变化受含水层倾角影响较小,随着泉口增大,水位变化受含水层倾角影响越大,这是由于当泉口较小时,落水洞水位变化主要受泉口大小的限制,对泉口大小的响应变化比较明显,而受含水层倾角影响较弱。总体而言,在泉口大小一定的条件下,含水层倾角越大,水位下降速率越快。
分析3组试验结果的不同点,对比分析不同含水层倾角条件下,落水洞水位变化特征可以发现,含水层倾角α=0°时,落水洞水位随时间呈阶梯形下降,如图4-19(a)~(c)所示,随着泉口的增大,阶梯状越来越不明显,甚至消失如图4-19(d)~(e)所示;而含水层有一定倾角(5°,8°)时,落水洞水位随时间呈直线状下降。含水层倾角不同,落水洞水位变化特征不同的原因在于,含水层倾角为0°时,水位下降呈阶梯状主要受层面裂隙影响,流入垂向裂隙的水,汇集至层面裂隙,相比在垂向裂隙中的水流,在层面裂隙中的水流流速减慢,而且有一部分水流入落水洞,经过层面裂隙的过渡,使得落水洞水位间断性下降变缓,即表现为图中的阶梯状,而含水层有一定倾角时,在重力的作用下,层面裂隙中的水流流速增大,弱化了层面裂隙的过渡作用,从而使得水位下降呈直线形而非阶梯形。

图4-26 不同含水层倾角条件下,水位下降速率与泉口之间的相关关系曲线图
