1.2.2 管道水流运动特征研究进展
19世纪初，科学工作者就已经发现圆管中液体流动时水头损失和水流流速之间有一定关系。直到1883年由于雷诺的试验，才使人们认识到水头损失与水流流速间的关系，是因为实际水流运动存在两种流态——层流和紊流，并提出将Re作为判别水流流态的依据。Re的物理意义可理解为惯性力与黏滞力之比，惯性力占主导地位，则Re较大；黏滞力占主导地位，则Re较小。经过对圆管的反复试验，提出以下判别标准：
层流：
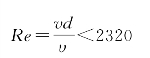
紊流：
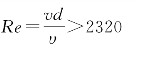
式中 d——圆管直径，m；
2320——圆管中的临界Re；
v——水流流速，m/s；
υ——运动黏滞系数，m2/s。
描述圆管流沿程水头损失与水流流速关系的达西-魏斯巴赫公式为
式中 hf——圆管中的沿程水头损失；
λ——沿程水头损失系数；
l——圆管长度；
d——圆管直径；
v——圆管中水流流速；
g——重力加速度。
该公式对于层流、紊流均适用。
1933年，Nikurades用试验系统地揭示了人工粗糙管沿程水头损失系数的变化规律，发表了圆管流情况下的试验结果。为了确定沿程水头损失系数λ随Re和相对粗糙度
的变化规律，Nikurades在圆管内壁粘贴上经过筛分、具有相同粒径Δ的砂粒，以制成人工均匀粗糙壁面，然后在不同相对
的管道上进行试验。该试验全面揭示了不同流态情况下λ、Re、
的关系，试验得到λ的变化规律如下：
（1）对于层流，λ仅仅是Re的函数，试验与理论均表明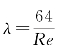
。
（2）对于紊流分为3种情况：①紊流光滑区，λ仅仅是Re的函数，即λ=λ（Re），且
；②紊流过渡粗糙区，λ是Re和
的函数，即
；③紊流粗糙区，λ仅仅是
的 函数，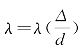
。
赵坚等（2005）在研究常用的圆管水流计算理论及经验公式后提出计算管道紊流条件下λ的改进方法。赵坚和赖苗提出由于临界区（指紊流和层流之间的临界区）的水流运动规律至今尚未研究清楚，为简化计算，将其并入紊流区。得到的管道沿程水头损失系数λ的计算公式为
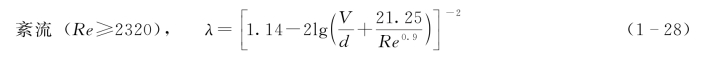
式（1-27）是一个适用于求解紊流3个区沿程水头损失系数λ的公式，它与达西-魏斯巴赫公式一起，可以分别计算出圆管水流四个分区（层流区、光滑紊流区、紊流过渡区和紊流粗糙区）中的沿程水头损失系数λ。
其他研究者对管流运动的研究，如Burman和Hanbo成功地应用斯托克斯方程和N-S方程描述了管道流运动。
综上所述，研究者对管道流的研究主要集中在过水断面为圆形的管道水流水力特性，而在众多相关资料中提到过水断面为矩形的管道流和裂隙流，对于管道流和裂隙流的区分大多是以开度为依据，裂隙开度较小，管道开度较大，即使有些研究中给出了裂隙和管道开度的划分范围，也并没有给出充足的划分依据。本书针对这一问题，基于水头损失测量结果，对比立方定律及达西-魏斯巴赫公式，对裂隙流和管道流的水力特性进行了识别，并分别用不同的水流运动方程进行描述。