4.3.1 落水洞水位对水文情景一的响应变化
4.3.1.1 含水层倾角为0°
裂隙网络-管道双重介质物理模型水平放置,即含水层倾角α=0°。
试验共设置8个不同的补给强度,主要研究含水层倾角α=0°条件下,落水洞水位对不同补给强度的响应变化。分析试验数据,得到不同补给强度条件下,落水洞水位随时间变化曲线,如图4-7所示。
图4-7中,落水洞水位变化曲线对应的补给强度Qre自左至右逐渐减小。从图4-7中可以看出,补给强度越大,含水层底部管道开始得到补给的时刻越早,落水洞水位开始上升的时间越早,即水流滞后时间越短,相应的落水洞水位上升越快。在同一补给强度条件下,随落水洞水位的不断上升,水位上升变化率减小,主要是由水流在裂隙网络中的滞后作用导致,补给到裂隙网络-管道含水介质的水流不能直接到达底部管道和落水洞,而是经过裂隙网络的“过滤”到达含水层底部管道和落水洞,由于相对于管道而言,裂隙网络的低渗透性,在含水层得到补给后,并非全部的水流直接到达底部管道和落水洞,在补给过程中始终有一部分水储存在裂隙网络中,而随着水位的上升,下部的裂隙网络-管道介质逐渐饱和,非饱和含水层部分的体积越来越小,从而非饱和区储存水量对于饱和区的补给量越来越少,因此导致水位上升变化率逐渐减小。
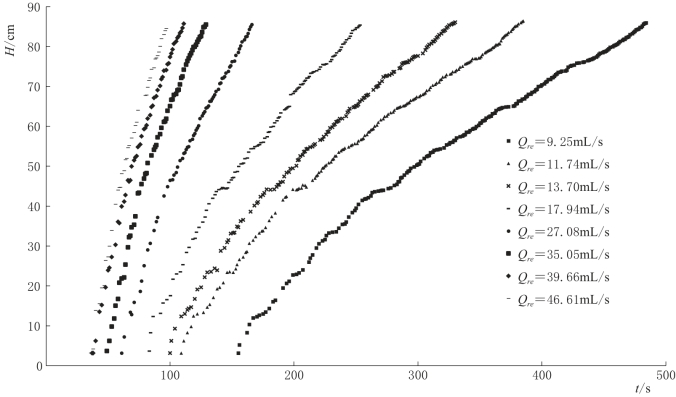
图4-7 不同补给强度条件下落水洞水位随时间变化曲线图(α=0°)
为进一步研究落水洞水位的变化规律,应用Matlab程序分别对这8条落水洞水位变化曲线进行拟合,拟合结果表明,落水洞水位与时间之间呈对数关系,计算式为
![]()
式中 H——落水洞水位,cm;
t——时间,s;
A——系数,cm/s;
B——系数,cm。
式(4-1)中,系数A与补给强度Qre变化密切相关,两者的关系可由直线表达,如图4-8所示。
![]()
而系数B与补给强度Qre之间无明显函数关系,在-293.72~-346.71变化,取其平均值,为-317.67,记为B0,用于数学模型的建立。
联合式(4-1)及式(4-2)可得落水洞水位变化表达式为
![]()
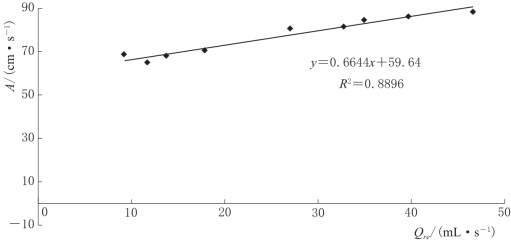
图4-8 系数A与补给强度Qre之间的相关关系曲线图(α=0°)
为修正由B0代替B带来的误差,引入修正系数h0。设Hti为补给强度为i,t时刻的落水洞水位,Htj由式(4-3)计算。而Hti-Htj为一常数,记为h0。h0与补给强度Qre之间存在二次函数关系,如图4-9所示。
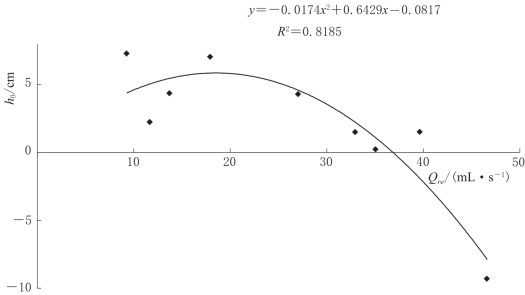
图4-9 修正系数h0与补给强度Qre之间二次函数关系曲线图(α=0°)
含水层倾角为0°条件下,落水洞水位对不同补给强度的响应变化的计算式为
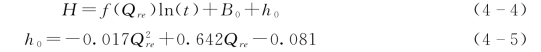
为验证式(4-4)的正确性,对补给强度Qre=23.07m L/s时的物理试验测量值与数学模型计算值进行对比,对比结果如图4-10所示。从图中可以看出,两者吻合度较高,因此该数学模型具有较高的可信度。
4.3.1.2 含水层倾角为5°
将裂隙网络-管道双重介质物理模型的落水洞一侧用玻璃支架垫高,使模型底部管道与水平方向成5°夹角,即含水层倾角α为5°。
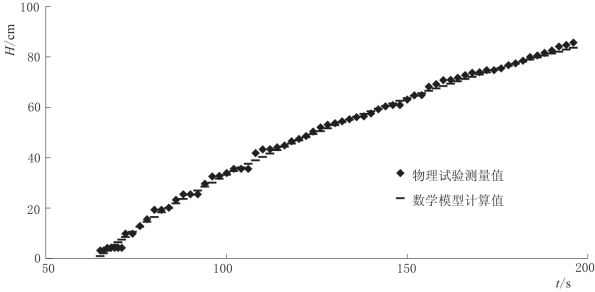
图4-10 物理试验测量值与数学模型计算值对比图(Qre=23.07m L/s)
试验共设置9个不同的补给强度,主要研究含水层倾角为5°条件下,落水洞水位对补给强度的响应变化。分析试验数据,得到不同补给强度条件下,落水洞水位随时间变化曲线如图4-11所示。
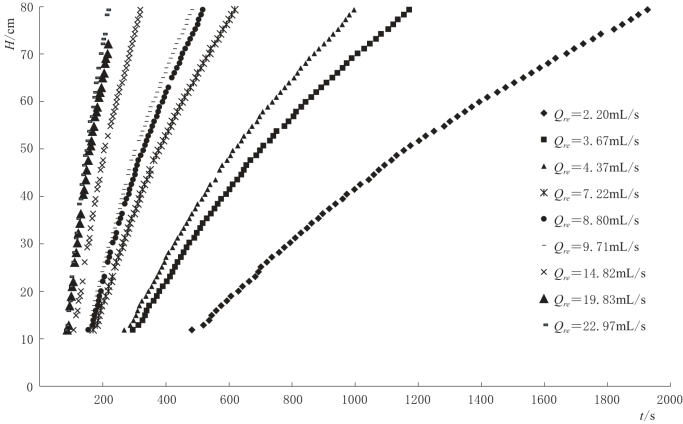
图4-11 不同补给强度条件下落水洞水位随时间变化曲线图(α=5°)
图4-11中,落水洞水位变化曲线对应的补给强度(Qre)自左至右逐渐减小。从图4-11中可以看出,补给强度越大,含水层底部管道开始得到补给的时刻越早,即水流滞后时间越短,响应的落水洞水位上升越快。在同一补给强度条件下,随落水洞水位的不断上升,水位上升变化率减小,减小的原因与本书第4.3.1.1节所述含水层倾角为0°的情况相同。与含水层倾角为0条件下的落水洞水位变化相比较,含水层有倾角时,落水洞水位随时间的变化曲线相对比较光滑,而含水层没有倾角时,落水洞水位的变化曲线比较粗糙,产生这一差异的原因可能是层面裂隙的过渡作用,含水层没有倾角时,层面裂隙的过渡作用比较强;而含水层有倾角时,由于水流流速的增大,层面裂隙的过渡作用减弱。
为进一步研究落水洞水位变化规律,利用Matlab程序分别对这9条落水洞水位变化曲线进行拟合,拟合结果表明,落水洞水位与时间之间呈二项式函数关系,表达式见式(4-6)。系数p1,p2,p3的拟合结果见表4-5。
![]()
式中 p1——系数,cm/s;
p2——系数,cm/s;
p3——系数,cm。
表4-5 式(4-6)系数拟合结果
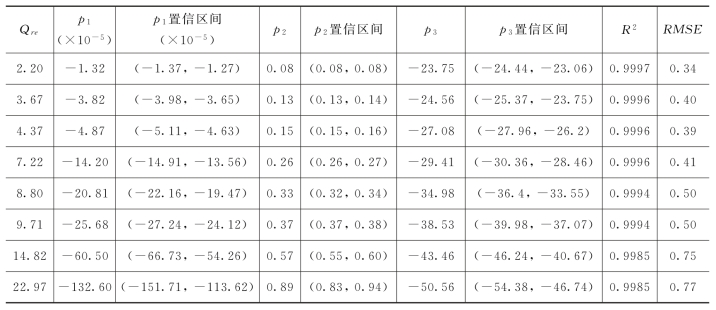 (https://www.daowen.com)
(https://www.daowen.com)
系数p1,p2,p3的取值与补给强度Qre密切相关,分析两者之间的相关关系,结果如图4-12所示,二次项系数p1随补给强度的增大而减小,两者之间的关系可由二次函数p1(Qre)刻画;一次项系数p2随补给强度的增大而增大,两者之间的关系可由一次函数p2(Qre)刻画;常数项随补给强度的增大而减小,两者之间的关系可由一次函数p3(Qre)刻画。
含水层倾角为5°条件下,落水洞水位对补给强度的响应计算式为
![]()
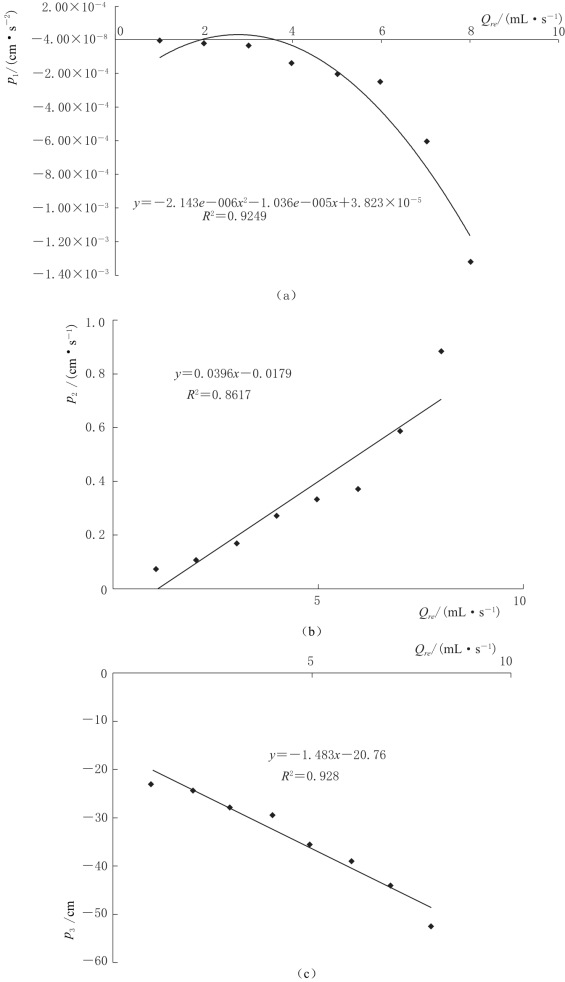
图4-12 系数p1,p2,p3值与补给强度之间的相关关系曲线图(α=5°)
为验证式(4-7)的正确性,对补给强度Qre=8.97m L/s时的物理试验测量值与数学模型计算值进行对比,对比结果如图4-13所示。从图中可以看出,两者吻合度较高,因此该数学模型具有较高的可信度。
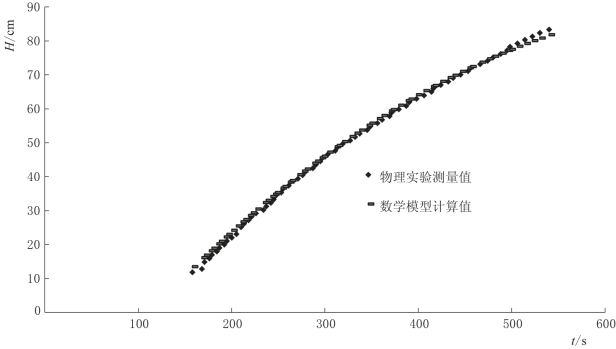
图4-13 物理试验测量值与数学模型计算值对比图(Qre=8.97m L/s)
4.3.1.3 含水层倾角为8°
将裂隙网络-管道双重介质物理模型的落水洞一侧用玻璃支架垫高,使底部管道与水平方向成8°夹角,即含水层倾角α=8°。
试验共设置9个不同的补给强度,主要研究含水层倾角为8°条件下,落水洞水位对补给强度的响应变化。分析试验数据,得到不同补给强度条件下,落水洞水位随时间变化曲线如图4-14所示。
图4-14中,落水洞水位变化曲线对应的补给强度(Qre)自左至右逐渐减小。从图4-14中可以看出,补给强度越大,含水层底部管道开始得到补给的时刻越早,响应的落水洞水位上升越快。在同一补给强度条件下,随落水洞水位的不断上升,水位上升变化率减小,减小的原因同本书第4.2.1.1节含水层倾角为0的情况。与含水层倾角为0时,落水洞水位的变化曲线相比,落水洞倾角为8°时,落水洞水位曲线变化比较光滑。
分别对这9条落水洞水位变化曲线进行拟合,拟合结果表明,与含水层倾角为5°时结果类似,落水洞水位与时间之间呈二项式函数关系,见式(4-8)。系数q1,q2,q3的拟合结果见表4-6。
![]()
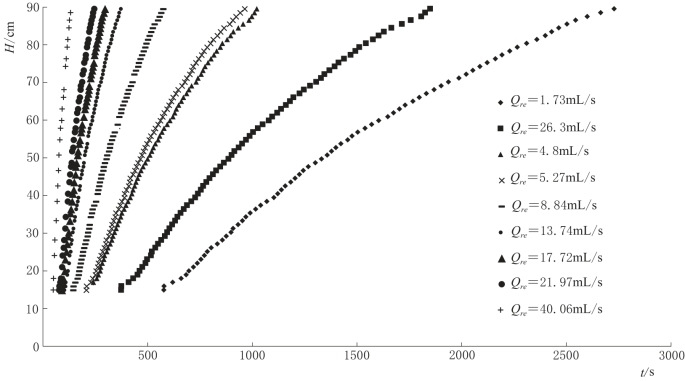
图4-14 不同补给强度条件下落水洞水位随时间变化曲线图(α=8°)
式中 q1——系数,cm/s2;
q2——系数,cm/s;
q3——系数,cm。
表4-6 式(4-8)系数拟合结果
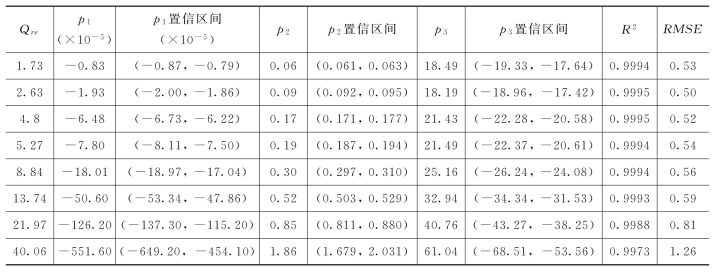
不同的补给强度对应不同的系数q1,q2,q3值,进一步分析两者相关关系,结果如图4-15所示,二次项系数q1随补给强度的增大而减小,两者之间的关系可由二次函数q1(Qre)刻画;一次项系数q2随补给强度的增大而增大,两者之间的关系可由一次函数q2(Qre)刻画;常数项q3随补给强度的增大而减小,两者之间的关系可由一次函数q3(Qre)刻画。
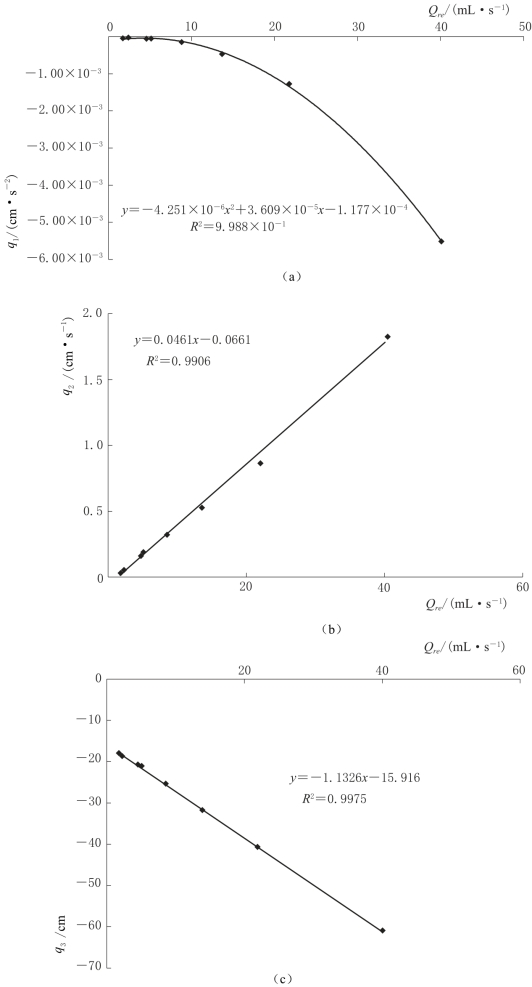
图4-15 q1,q2,q3值与补给强度之间的相关关系曲线图(α=8°)
含水层倾角为8°条件下,落水洞水位对补给强度的响应计算式为)
![]()
为验证式(4-9)的正确性,对补给强度Qre=17.72m L/s时的物理试验测量值与数学模型计算值进行对比,如图4-16所示。从图中可以看出,两者吻合度较高,因此该数学模型具有较高的可信度。
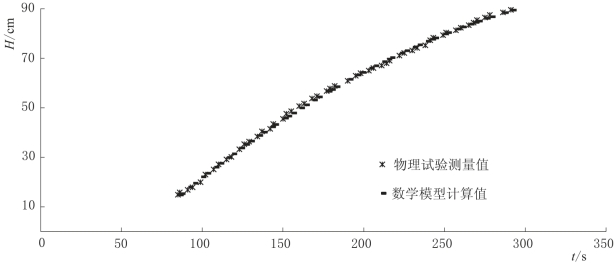
图4-16 物理试验测量值与数学模型计算值对比图(Qre=17.72m L/s)
4
.3.1.4 对照试验
为更好地理解裂隙网络-管道双重介质对落水洞水位变化的影响,设置几组对照试验。对照试验中,由有机玻璃制成的直径为24.2cm的圆形水桶代替裂隙网络-管道含水介质物理模型。试验中设置5个不同的补给强度,进行相同的试验操作,如图4-17所示。试验结果表明,没有裂隙网络-管道介质的影响,水位随时间呈直线变化,而且补给强度越大,直线斜率越大,即水位上升越快。
在同一补给强度条件下,水位上升速率不变。水位变化可由式(4-10)表达,式中Qre以及S均为定值。

4.3.1.5 结果对比分析
首先分析3组试验结果的相同点,无论含水层有无倾角,补给强度越大,落水洞水位上升速率越大;在同一补给强度条件下,随落水洞水位的不断上升,水位上升变化率均减小。原因在于试验过程中裂隙网络对水流的过滤作用导致水流滞后,使一部分水量暂时储存在裂隙网络中,而在试验过程中,随着水位的上升,未饱和部分对饱和部分的补给越来越少,从而使水位上升变化率减小。
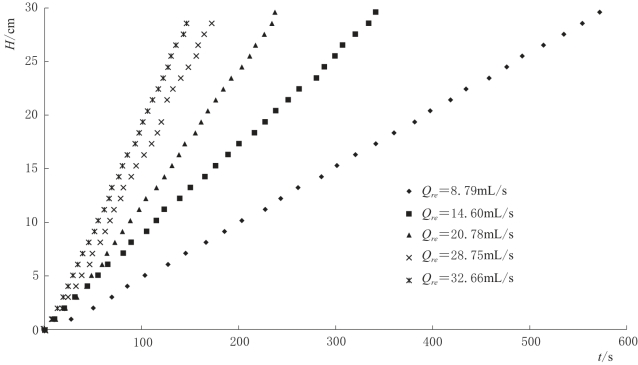
图4-17 水文情景一对照试验结果图
然后分析3组试验结果的不同点,含水层倾角为0°时,不同补给强度条件下,落水洞水位与时间之间呈对数函数关系,且水位变化曲线比较粗糙;含水层有一定倾角(5°,8°)时,不同补给强度条件下,落水洞水位与时间之间呈二次多项式函数关系,而且相对于含水层倾角为0°,水位变化曲线比较光滑,导致落水洞水位变化特征不同的原因可能在于,层面裂隙的过渡作用,含水层倾角为0°时,层面裂隙的过渡作用比较强;而含水层有倾角时,由于水流流速的增大,层面裂隙的过渡作用减弱。
将含水层倾角为5°、8°的试验结果做对比分析,落水洞水位二次函数表达式系数随补给强度变化如图4-18所示。从图中可以看出,p1(Qre)<q1(Qre),p2(Qre)>q2(Qre),p3(Qre)<q3(Qre),对比分析结果表明,含水层倾角越大,在相同的补给强度条件下,同一时刻,落水洞水位越高。
