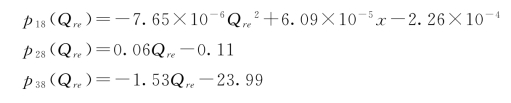4.5.1　管道水头对水文情景一的响应变化

4.5.1　管道水头对水文情景一的响应变化

不同补给强度，不同含水层倾角条件下，管道水位随时间变化如图4-40所示。研究结果表明，无论模型有无倾角，补给强度越大，管道水头增大越快。模型倾角一定时，补给强度的大小并不影响水头上升的模式。而模型倾角影响水头上升数学模型，模型倾角α=0°时，管道水头随时间呈对数变化，模型倾角α=5°或者α=8°时，管道水头随时间呈二次函数关系变化。

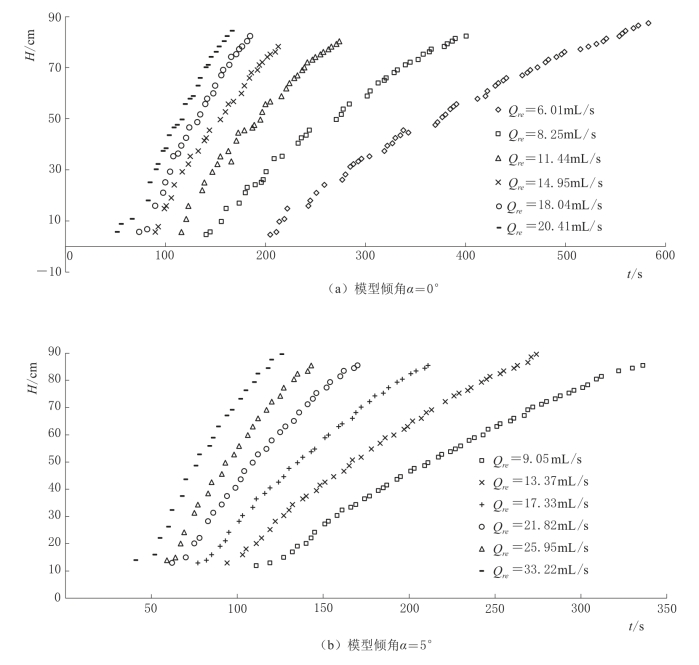
图4-40（一）　不同补给强度，不同含水层倾角条件下，管道水位随时间变化曲线图

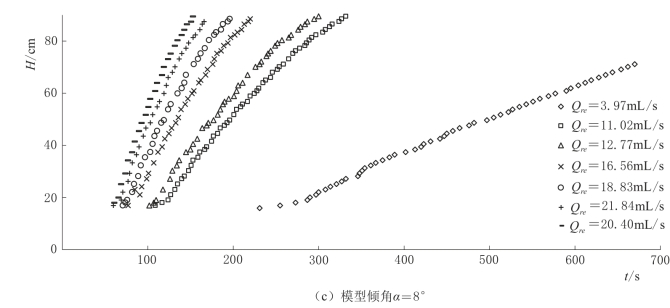
图4-40（二）　不同补给强度，不同含水层倾角条件下，管道水位随时间变化曲线图

利用统计分析法，分别得到模型倾角α=0°，5°，8°时，管道水头变化函数关系为模型倾角α=0°时，

其中，系数A与补给强度的相关关系如图4-41所示。

A（Qre）=0.52Qre+76.06，B=-384.57

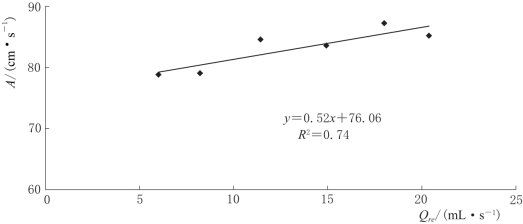
图4-41　系数A与补给强度Qre之间的相关关系曲线图（α=0°）

模型倾角α=5°时，

其中，系数p15，p25，p35与补给强度的相关关系如图4-42所示。

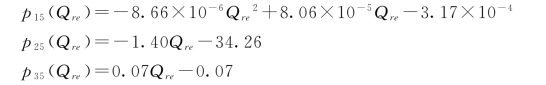
模型倾角α=8°时，

其中，系数p18，p28，p38与补给强度的相关关系如图4-43所示。

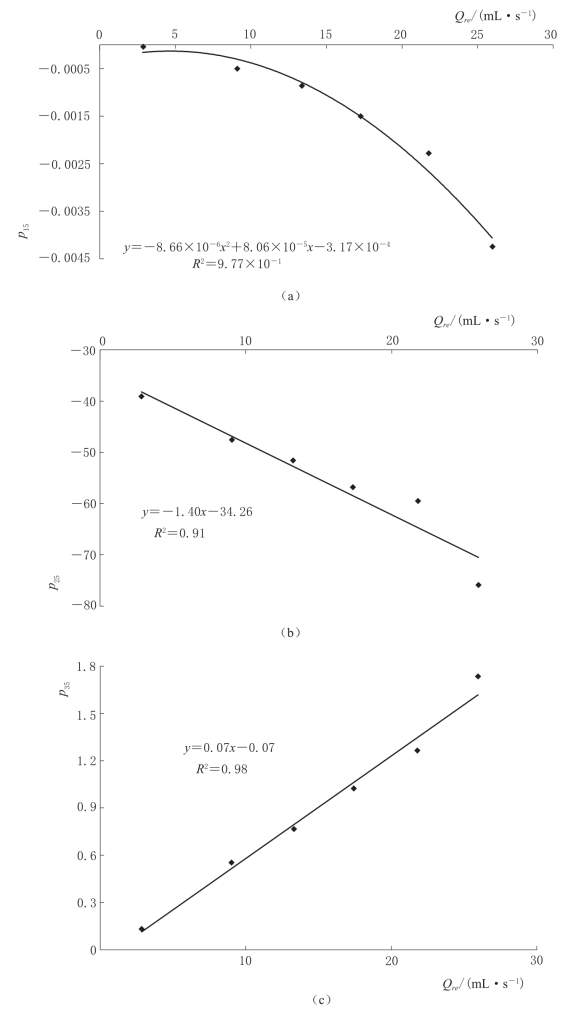
图4-42　系数p1，p2，p3与补给强度之间的相关关系曲线图（α=5°）

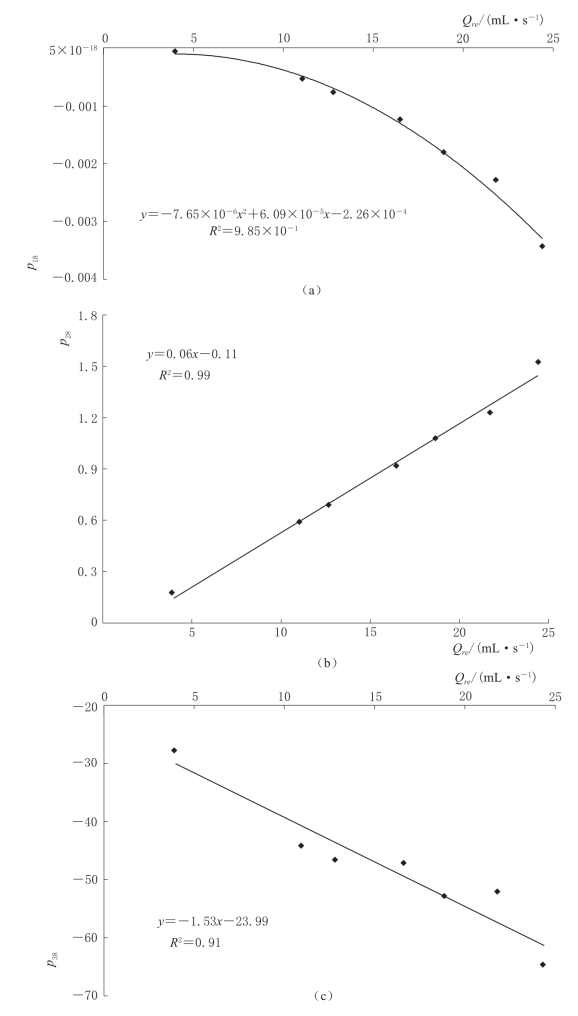
图4-43　系数p1，p2，p3与补给强度之间的相关关系曲线图（α=8°）