3.2.4　结果分析

3.2.4.1　试验结果与理论公式对比

不同尺寸的裂隙或管道中对应的临界流速，见表3-1。由临界流速可知，试验中的水流既有层流又有紊流。从图3-6中可以看出，当开度b≤1.4635mm时，水头损失与水流流速之间呈线性关系；当开度b≥1.8375mm时，水头损失与水流流速之间呈非线性关系；当开度b=1.6000mm时，水头损失与流速之间的关系处于线性与非线性之间。

对于开度b＞1.4635mm的裂隙（即W=3cm，b=2.8575mm；W=3cm，b=1.8375mm及W=2cm，b=1.9275mm），对于水头损失hf与水流流速v之间的关系作v=eJm和hf=avc两种形式的拟合，拟合结果见表3-2。

表3-2　v=e Jm和hf=avc中指数m和c拟合结果

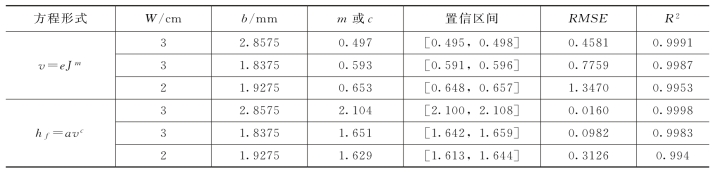
根据达西-魏斯巴赫公式，当b＜1.4635mm时，c在1附近，即水头损失与流速之间呈线性关系，因此，其中的水流属于层流；当开度b＞1.8375mm时，c＞1，水头损失与流速之间呈非线性关系，因此，其中的水流属于紊流。根据临界Re判断，当水流流速小于临界流速时，水流属于层流，水头损失与流速之间呈线性关系；当水流流速大于临界流速时，水流属于紊流，水头损失与流速之间呈非线性关系。但是，在本书试验中，裂隙尺寸为W=3cm，b＞1.5mm以及W=2cm，b=1.9275mm的试验结果中，即使水流流速小于临界流速，水头损失与水流流速也呈非线性关系；而在裂隙尺寸为W=2cm，b=1.3850mm的试验结果中，即使水流由层流变为紊流，水头损失与水流流速之间依然呈线性关系。这些试验结果与之前所认为的“层流状态下，水流服从达西定律和立方定律，即水头损失与流速呈线性关系；紊流状态下，水流不服从达西定律和立方定律，即水头损失与流速呈非线性关系”不符。而且，由临界Re划分的水流流态结果与由达西-魏斯巴赫公式得到的结果相矛盾。可能的解释是，W≤1.4635mm的裂隙中的水流与裂隙宽度W≥1.8375mm的裂隙中的水流为两种不同类型的水流。裂隙宽度W≤1.4635mm时，水头损失与水流流速呈线性关系，服从达西定律及立方定律，呈现裂隙流特性。裂隙宽度W≥1.8375mm时，水头损失与水流流速呈非线性关系，不服从达西定律及立方定律，呈现管道流特性。开度b=1.6000mm时，水流处于裂隙流与管道流的过渡区。得到这一结论是基于裂隙管道的区别在于开度不同，开度较小的为裂隙，开度较大的为管道。本次试验结果可以看出，随着开度的增大，水头损失与水流流速之间的线性程度降低。因此，可将裂隙定义为开度b≤1.4635mm，管道定义为开度b≥1.8375mm。

3.2.4.2　试验结果与其他研究结果对比

钱家忠等（2005）年，以开度为2～6mm的裂隙为研究对象，通过室内物理试验，主要对开度及壁面粗糙性（细、中粗、粗）对水流运动的影响进行了研究。钱家忠等（2005）得出水流流速与水力坡度之间呈指数关系v=e Jm，并且指数在0.5附近波动。在本次试验中，当开度b≥1.8375mm，指数m均值为0.58，与钱家忠等得到的试验结果相似。