4.4 落水洞水位变化公式推导
以裂隙网络-管道双重介质底部管道中线所在平面为基准面。以裂隙网络-管道双重介质中水位所在平面为研究断面1—1',取垂直于泉口出流口的断面为研究断面2—2',如图4-36所示。由试验数据分析以及试验观测结果得到裂隙网络水位与落水洞水位变化相一致,故可作以下推导。
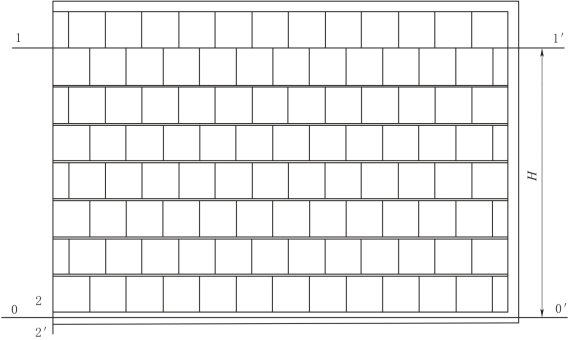
图4-36 裂隙网络-管道双重介质装置研究断面选取示意图
对断面1—1'和断面2—2'列能量方程为
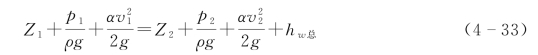
进一步可以得到落水洞水位表达式为

式中 hw总——裂隙网络-管道双重介质模型总的水头损失。
裂隙网络-管道双重介质模型可以分解为若干个平行裂隙,倒T形裂隙和正T形裂隙,如图4-37所示。整个模型的水头损失也就由平行裂隙的沿程水头损失以及倒T形裂隙和正T形裂隙的局部水头损失组成。平行裂隙的沿程水头损失在本书第3章已经做了相关研究,下面来推导倒T形裂隙和正T形裂隙部分的局部水头损失。
首先取倒T形裂隙的![]() 为研究对象,如图4-38所示。由动量守恒和能量守恒方程,推导水流经过倒T形裂隙时的水头损失。
为研究对象,如图4-38所示。由动量守恒和能量守恒方程,推导水流经过倒T形裂隙时的水头损失。
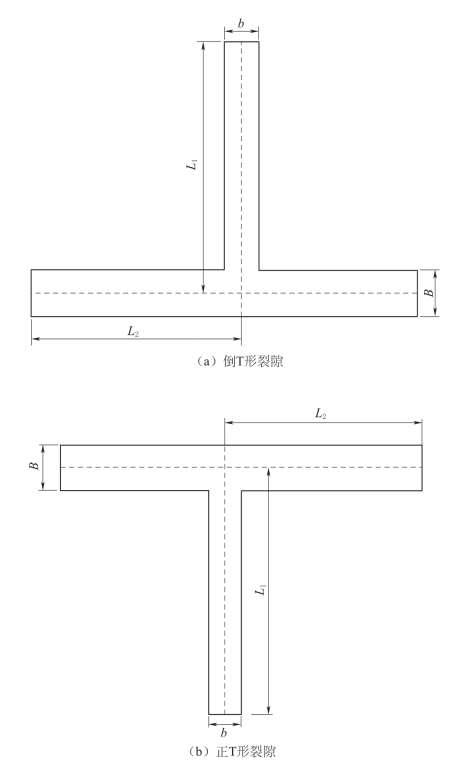
图4-37 倒T形裂隙以及正T形裂隙示意图
取1—1'断面及2—2'断面间的流体为研究对象,列动量方程和能量方程。
沿x轴方向的动量守恒方程为
![]()
沿Y轴方向的动量守恒方程为
![]()
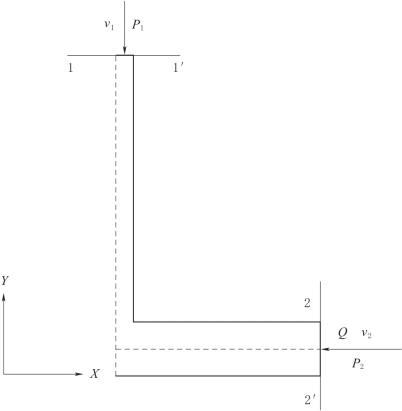
图4-38 倒T形裂隙研究断面示意图
由能量方程得(https://www.daowen.com)
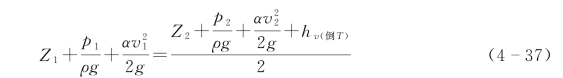
将重力表达式![]() 代 入以上3个方程,并联合式(4-35)~式(4-37)可得
代 入以上3个方程,并联合式(4-35)~式(4-37)可得
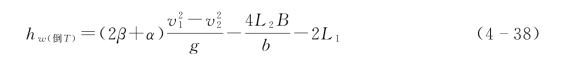
或者
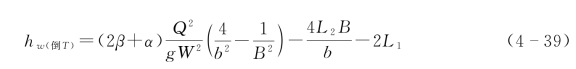
取正T形裂隙的![]() 为研究对象,如图4-39所示。由动量守恒和能量守恒方程,推导水流经过正T形裂隙时的水头损失。
为研究对象,如图4-39所示。由动量守恒和能量守恒方程,推导水流经过正T形裂隙时的水头损失。
以1—1'断面及2—2'断面间的流体为研究对象,列动量方程和能量方程。
沿x轴方向的动量守恒方程为
![]()
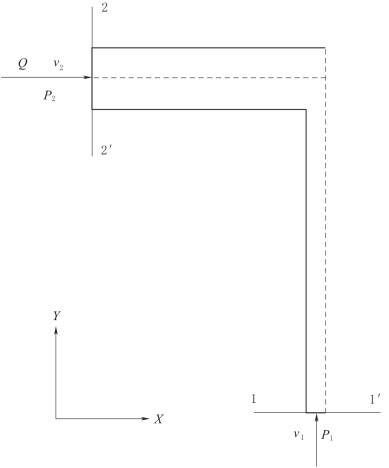
图4-39 正T形裂隙研究断面示意图
沿Y轴方向的动量守恒方程为
![]()
由能量方程得
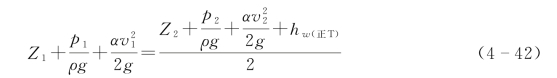
将重力表达式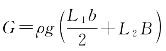 ,水流流速表达式
,水流流速表达式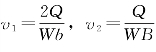 代 入以上3个方程,并联合式(4-40)~式(4-42)可得
代 入以上3个方程,并联合式(4-40)~式(4-42)可得
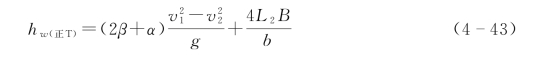
或者
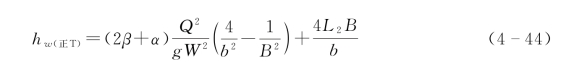
裂隙平行部分的水头损失由修正立方定律或者达西-魏斯巴赫公式进行计算。裂隙折角处的局部水头损失hj(倒T)可由总水头损失hw(倒T)减去沿程水头损失hf得到。
