Ⅱ

Ⅱ

在哥本哈根安顿下来以后，我和卢瑟福保持了密切的接触，我定期地向他报告了我在曼彻斯特已经开始的关于一般原子问题的工作进展。卢瑟福的复信总是很鼓舞人的，这些复信的共同点就是当谈到他的实验室中的工作时的那种主动性和兴致勃勃。这事实上是历时25年的长期通信的开始；每当翻阅这些信件时，我都会重新想起卢瑟福对他所开辟的领域中的进步所抱的热诚，以及他对试图在该领域中有所贡献的任何人的努力所感到的热烈兴趣。

我在1912年秋季写给卢瑟福的那些信件，谈到了追寻作用量子在卢瑟福原子的电子结构中所起的作用的持续努力，其中也包括分子键合的问题和辐射效应及磁效应的问题。但是，稳定性问题在所有这些考虑中引起了纠缠不清的困难，这些困难刺激着我们去寻求更坚实的立脚点。然而，经过按更一致的方式来应用量子概念的各式各样的尝试以后，我在1913年的初春才认识到，直接适用于卢瑟福原子的稳定性问题的一个线索，是由支配着元素光谱的惊人简单的定律提供出来的。

在罗兰（Rowland）等人对谱线波长的极端精确的测量的基础上，在巴耳末（Balmer）的贡献和卢瑟福在曼彻斯特的前任教授舒斯特（Schuster）的贡献之后，普遍的光谱定律已由里德伯（Rydberg）最巧妙地搞清楚了。彻底分析线光谱中的主要线系及其相互关系的主要结果，就在于认识到已知元素的光谱中每一谱线的频率v都可以无比精确地写成v=T'-T"，式中T'和T"是作为元素之特征的许多谱项中的两项。

这一基本的并合定律显然不能有普通的力学解释，而且，可以很有兴趣地回想起，瑞利勋爵（Lord Rayleigh）在这方面曾经怎样恰当地强调过下述事实：一个机械模型的各个简正振动模式的频率之间的任何普遍关系，应该是各该频率的二次式而不是它们的一次式。对于卢瑟福原子来说，我们甚至不能期望有什么线光谱，因为，按照普通的电动力学，伴随着电子运动的辐射，其频率应该随着能量的发射而连续变化。因此，很自然地可以试图将光谱的解释直接建筑在并合定律的基础上。

事实上，接受了爱因斯坦关于能量为hv（h是普朗克恒量）的光量子或光子的概念，人们不免就要假设，原子对辐射的每一发射或吸收，都是由一个能量传递h（T'-T"）所伴随的一次个体过程，并将hT解释为原子的某种稳定状态中或所谓定态中的电子结合能。特别说来，这一假设给线系谱中各发射谱线及吸收谱线的表观奇特性提供了直截了当的解释。例如，在发射过程中，我们看到的是原子从高能级到低能级的跃迁，而在吸收过程中，我们遇到的则一般是原子从具有最低能量的基态到它的一个受激态的跃迁。

在氢光谱这一最简单的情况中，各谱项可以很精确地表示为Tn=R/n2，式中n是一个整数，而R是里德伯恒量。这样，上述解释就导致氢原子中电子结合能的一系列递减的值；这指示着一种跨步式的过程；通过这种过程，原来离核很远的电子将通过辐射跃迁而进入用越来越低的n值表征着的结合得越来越牢固的定态，直到达到了用n=1来标志的基态为止。此外，将这一定态的结合能和沿着开普勒（Kepler）轨道绕核运动的电子的能量相比较，所得到的轨道线度是和由气体属性推得的原子线度具有相同数量级的。

在卢瑟福原子模型的基础上，这一观点也直截了当地为里德伯恒量在其他元素的更复杂光谱中的出现提示了解释。例如，我们得到结论，这儿遇到一些涉及原子受激态的跃迁过程；在这种受激态中，有一个电子被弄到结合在核周围的其他电子所占的区域以外去了，因此这个电子就受到和单位电荷周围的力场相似的一个力场的作用[3]。

探索卢瑟福原子模型和光谱资料之间的更密切的关系，很明显地带来了一些烦难问题。一方面，电子和原子核的电荷及质量的定义本身，是完全建筑在依据经典力学原理和经典电动力学原理对物理现象进行分析的基础上。另一方面，认为原子内能的任何改变都是二定态间的完全的跃迁，这种所谓量子公设就排除了按照经典原理来说明辐射过程或说明涉及原子稳定性的任何其他反应的可能性。

正如我们今天所知道的，这种问题的解决要求发展一种数学表述形式，其恰当诠释蕴涵了对无歧义地应用基本物理概念的基础的根本修正，蕴涵了对于在不同实验条件下观察到的各种现象之间的互补关系的认识。但是，在当时，仍可利用经典物理图景来在定态的分类方面取得某种进步，这种分类是以关于谐振子能态的普朗克原始假设为基础的。特别说来，更仔细地比较频率已定的振子和电子以依赖于结合能的公转频率而绕核进行的开普勒运动，就能得到一个分类的出发点。

事实上，正如在谐振子情况下一样，简单的计算表明，对于氢原子的每一定态来说，可以令在电子的一个轨道周期中求出的作用量积分等于nh，这一条件在圆形轨道的情况下和角动量以h/2π为单位的量子化相等效。这种相等关系使我们可以用电子电荷e、电子质量m和普朗克恒量将里德伯恒量表示出来，所遵循的公式是：

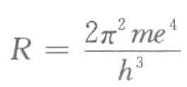
在当时可用的e、m和h的测量结果的精确范围内，我们发现这一结果和R的经验值是一致的。

虽然这种一致性指示了应用力学模型来把定态形象化的适用范围，但是，量子概念和普通力学原理的任何结合都会涉及的那些困难当然还是存在着的。因此，最令人放心的就在于发现了下述事实：光谱问题的全部处理方式，满足一种明显的要求，即它可以包括经典描述，作为所涉及的作用量够大以致可以忽略单个量子的那种极限情况。这种考虑确实提供了所谓对应原理的初次指示，该原理的目的在于将量子物理学的本质上是统计性的说明，表示成经典物理描述的合理推广。

例如，在通常的电动力学中，从一个电子体系发出的辐射的成分，应该取决于将体系的运动分解成谐振动时所能得到的那些频率和振幅。当然，在电子绕重核的开普勒运动和由体系定态间的跃迁所发射的辐射之间，是不存在这样的简单关系的。然而，在一种极限情况，即对于量子数n的两个值远大于它们的差数的那种跃迁，却可以证明，作为一些无规的个体跃迁过程的结果而出现的辐射，其成分谱线的频率是和电子运动的谐振动分量的频率渐近地重合的。而且，在开普勒轨道中，不同于简谐振动，除了公转频率以外还会出现较高的泛频，这一事实就提供了给氢光谱中各谱项的任意并合寻求一种经典案例的可能性。

但是，卢瑟福原子模型和光谱资料之间的关系的明确证实，却在一段时间内受到一种奇特情况的阻碍。早在二十年前，匹克灵（Pickering）就曾经在遥远星体的光谱中观察到一个线系，其中各谱线的波长和普通氢光谱中的波长显示着很密切的数值关系。因此，这些谱线一般被认为属于氢，甚至里德伯也这样认为，其目的是要消除氢光谱的简单性和包括最接近氢光谱的碱金属光谱在内的其他元素光谱的复杂性之间的明显对立。就连杰出的光谱学家A.否勒也持有这一观点，当时他刚刚在用充有氢氦混合气体的放电管做的实验室实验中观察到了匹克灵线及新的有关线系。

然而，匹克灵谱线和否勒谱线不能包括在适用于氢光谱的里德伯公式中，除非允许谱项表示式中的数n既可以取整数值又可以取半整数值；但是，这种假设却将明显地破坏向能量和光谱频率间的经典关系的渐近式的趋近。另一方面，这种对应性对于另一种体系的光谱却是仍然适用的，该体系由一个电子和一个电荷为Ze的核组成，其定态由相同的一些作用量积分值nh来确定。事实上，这种体系的谱项应表为Z2R/n2，这一表示式在Z=2的情况下将和在里德伯公式中引用半整数n值时得出相同的结果。于是，很自然地可以认为，匹克灵谱线和否勒谱线属于被星体中或否勒所用放电管中的强烈热骚动所电离了的氦。事实上，如果这种结论得到证实，那就是已经向着依据卢瑟福模型来建立不同元素的属性之间的定量关系迈出了第一步。